Development of a Human-Machine System in the Form of a Person in a Passive Exoskeleton with Two Types of Spring Elements

The proposed model of the protective passive exoskeleton with spring elements addresses the following problems: autonomous working of exoskeleton while keeping some of the advantages of active exoskeletons and increasing the user comfort, unloading the human musculoskeletal system and protecting it. The proposed model differs from the existing [1- 3] ones by the availability of variable-length links [4-6]. These links enhance the comfort of the user operating the exoskeleton and make this operation more energy-efficient as the exoskeleton features the energy recuperators of two types: torsion and compression springs. These features make the consumer properties of passive exoskeletons close to those of active exoskeletons, although the designs of the former ones are simpler and cheaper.

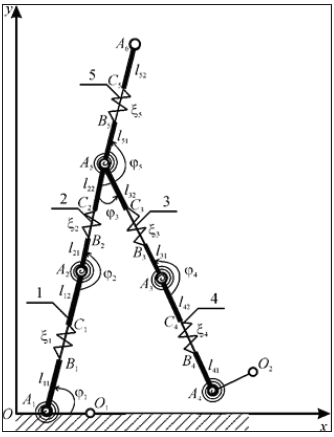
The passive exoskeleton with spring elements consists of variable-length links Figure 1 connected with cylindrical hinges. A variable-length link consists of the weightless spring and the two weighty absolutely rigid parts with lengths l_ij (i = 1,2, …., 5; j = 1,2), which perform the relative motion along the line passing through the beginning and the end of the link. The link length variability is implemented through the relative motion of the weighty parts along the link on the section В_iC_i = x_i(t) (i = 1,2, …., 5). In the double subscripts of the weighty link parts, the first index i corresponds to the link number, the second one j - corresponds to the number of the weighty link section. In the hinges-joints the torsion springs are installed to store and subsequently release the energy of the human musculoskeletal system. The feet are assumed to be weightless, absolutely rigid, connected to the links simulating the shins. The feet ensure the required contact with the surface without slippage. The hinges have bearings which ensure the relative rotation of exoskeleton links with minimal friction which is neglected in this research. The state of the mechanism is defined by the angles between the links j_i(t) and by the variable lengths of the link sections x_i(t) (i = 1,2, …., 5). Hence, the exoskeleton model has ten degrees of freedom. The masses of the absolutely rigid link sections A_iB_i are m_i1, the moments of inertia relative to the axes passing through their mass centres perpendicular to the motion plane are I_i1. The masses of the С_iA_i±1 sections are m_i2, the moments of inertia relative to the axes passing through their ends perpendicular to the motion plane are I_i2. The density of the material from which the j-th weighty section of the i-th link is made is r_ij (i = 1,2, …., 5; j = 1,2). The kinetic energy of the link is the sum of the kinetic energies of the weighty link sections A_iB_i and С_iA_i±1, which perform a complex motion: rotational around the mobile pole at the attachment point to the preceding link and translational along the link Figure 1.

The following should be done to solve the problem of simulating the motion of a person in a passive exoskeleton with spring elements of two types:
A. Build the system of differential equations of motion for the model shown on the Figure 1.

Figure 1:2-D model of passive exoskeleton with spring elements and angles calculated between the links.

B. Solve the Cauchy problem numerically for the derived system of differential equations of motion taking into account the exoskeleton mass and the given control based on the empirical information [5].
C. For a visual estimation of the obtained motion of the humanmachine robotic system as a person in exoskeleton, synthesize the animated visualization of the motion for the developed model based on the numerical solution of the Cauchy problem.

The system of differential equations of the mechanism motion similarly as it is described in the [4,5]. In the vector-matrix record it keeps the form (1), however, the matrices included into this equation become more cumbersome than in the case when the angles are calculated from the horizontal [4,5]. The matrix subscripts designate the corresponding generalized coordinate: k = 1, 2, here 1 corresponds to the generalized coordinate j, 2 - corresponds to the generalized coordinate ξ

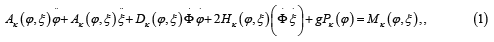
here: j = (j₁, …, j_n)^Т - the vector of angular generalized coordinates; ξ = (ξ₁, …, ξ_n)^T - the vector of generalized coordinates describing the lengths change of the links; - the vector of angular velocities; - the vector of angular accelerations; - the diagonal matrix; A_k, D_k - the matrices taking into account the inertia properties; P_k - the matrices defined by the moments of the gravity forces; H_k, A_k - the matrices taking into account the variable link lengths; M_k - the vectors of the generalized forces. We will apply the controlling torques empirically defined on a human [5] for numerical simulation of the controlled motion of a person in passive exoskeleton. Unlike to the available researches [4-6], the studied model has a different design of variable-length links. Additional springs, which are energy recuperators, have been added to hinges and links Figure 1. The values of the parameters used in the calculations are listed below. The initial lengths of the non-deformed links are as follows: l₁^* = l₄^* = 0.385m, l₂^* = l₃^* = 0.477m, l₅^* = 0.771m. These lengths are distributed on the link as follows: l₁₁ = l₄₁ = 0.15m, ξ₁^* = ξ₄^* = 0.085m, l₂₁ = l31 = 0.2m, ξ₂^* = ξ₃^* = 0.077m, l₅₁ = 0.3m, ξ₅^* = 0.171m, l_i1 = l_i2 (i = 1, …, 5). It is assumed that the exoskeleton mass amounts to 50% of the mass of every link of the human musculoskeletal system. Therefore, the masses of the human links m₁ = m₄ = 2.91kg, m₂ = m₃ = 8.93kg, m₅ = 28.93kg, are multiplied by 1.5 and are evenly distributed between the two weighty absolutely rigid link sections, i.e. m_i1 = m_i2 = m_i/2 (i = 1, …, 5). The moments of inertia of the weighty link sections for the rods relative to the axes passing through the bottom point of the weighty link sections are I₁₁ = I₄₁ = 0.011kg·m², I₂₁ = I₃₁ = 0.060kg·m², I51 = 0.434kg·m², I_i1 = I_i2 (i = 1, …, 5). They are multiplied by 1.5. In such a way, the inertial properties of the human-machine system were approximated. The acceleration due to gravity is g = 9.81m/s². The period of the single-support step phase, i.e. the half of the walking period is t_k = 0.36s. The animated visualization frames of the developed model motion based on the numerical solution of the Cauchy problem are shown on the Figure 2. On the animated frames of the mechanism motion, the weightless parts of variable-length links are shown with thin segments. The thick segments denote the weighty absolutely rigid parts of the links Figure 2.

Figure 2:The animated visualization frames of the protective passive exoskeleton motion.

Thus, there is an option to visually evaluate the motion of the proposed model. The Figure 2 illustrates the power of this approach and demonstrates the movements’ adequacy of the robotic human-machine system as a person in the protective exoskeleton.

The model of passive exoskeleton with variable-length links and spring elements, in which the angles are calculated between the links, has been proposed. This model is more prospective for building a working exoskeleton in which the controlled change of angles between the links should be implemented. The efficiency of this model, as well as its connection with the previous models, in which the angles are calculated between the links and the horizontal, are demonstrated.

1. https://karfidovlab.com/projects/exochair/
2. https://www.exoatlet.com/
3. Tsukahara A, Hasegawa Y, Eguchi K, Sankai Y (2015) Restoration of gait for spinal cord injury patients using HAL with intention estimator for preferable swing speed. IEEE Transactions on Neural Systems and Rehabilitation Engineering 23(2): 308-318.
4. Borisov AV, Rozenblat GM (2018) Modeling the dynamics of an exoskeleton with control torques in the joints and a variable length of the links using the recurrent method for constructing differential equations of motion. Journal of Computer and Systems Sciences International 57(2): 319-347.
5. Borisov AV, Rozenblat GM (2017) Matrix method of constructing the differential equations of motion of an exoskeleton and its control. Journal of Applied Mathematics and Mechanics 81(5): 351-359.
6. Borisov AV, Chigarev AV (2020) The causes of a change in the length of a person’s link and their consideration when creating an exoskeleton. Biomed J Sci & Tech Res 25(1): 18769-18771.