A Control of Logistic Model of Bladder Cancer with Dimensionless Estimate Parameters

Cancer is a class of diseases characterized by out-of-control cell growth. More dangerous, or malignant, tumors form when two things occur: 1) a cancerous cell manages to move throughout the body using the blood or lymphatic systems, destroying healthy tissue in a process called invasion. 2) That cell manages to divide and grow, making new blood vessels to feed itself in a process called angiogenesis. When a tumor spreads and invades to the body it destroys other healthy tissues, know as metastasized. This process is itself called metastasis; this stage is difficult to cure. According to the American Cancer Society, Cancer is the second most common cause of death in the US and accounts for nearly 1 of every 4 deaths [1].

Bladder cancer is a form of cancer that commonly begins in the cells lining the bladder, also known as transitional epithelium. Hematuria is the most common symptom of bladder cancer. Some cases of bladder cancer can only be detected through urine testing. Bladder cancer is commonly found in older people, with people over 55 making up about 90% of diagnosed cases. The common type of bladder cancer is transitional cell carcinoma. Bladder cancer risk factors include: Bladder defects from birth, Chemotherapy and radiation therapy, Chronic bladder infections and irritations, Exposure to certain chemicals including aromatic amines, Low fluid consumption, Personal or family history. Back pain can be a symptom of bladder cancer that has advanced from its original position in the bladder [2,3]. The purpose of this work to check the controllability and observability of mathematical model that describes tumor-immune interactions in the bladder as a result of BCG therapy. Numerical simulation carried out with dimensionless parameters to show the control behaviour.

We describe the interaction between tumor cells within the bladder, the immune system, and the BCG immunotherapy with a system of nonlinear ordinary differential equations. In our model the tumor cells are divided into two subpopulations; those that have been infected (T_i) with BCG (B) and those that are still uninfected T_u and susceptible. As the tumor cells are divided into two pools, the total number of tumor cells is given by: T=T_i +T_u. Since effector cells (E) target and destroy infected tumor cells (T_i) the latter must decrease at an intensity that is proportional to their encounter. By taking random mixing as a first approximation, the encounter rate is proportional to the product p3ETi, where p3 is a rate constant. Similarly, tumor cells become infected with BCG at a rate proportional to the product p₂ BT_u where p₂ is a rate coefficient. Thus the dynamics of the individual pools of tumor populations, the tumor growth factor in this model is given by:

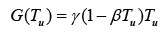
where γ is the growth rate of tumor cells, and β is the death of tumor cells as a result of self-limiting competition for resources such as oxygen and glucose. β-1 may be viewed as the maximum carrying capacity of the tumor under logistic growth [4-6].

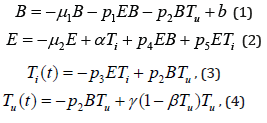
The parameters values of exponential model and logistic model for human are given in the table. Note that dimensionless estimates are obtained form source value using transformation [6].

A mathematically linear control system is given by the following two equations

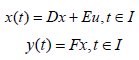
where x(t)∈Rⁿ , u(t)∈R^p and y(t)∈R^k for t∈I . I is closed interval. Elements of matrices are in L² (I, R).u(⋅)∈L2(I, R^p ) is called input/control, y(⋅)∈L2(I, Rk ) is called output and x(t)∈Rn , t∈I is called state [7-9,10]. If we consider the BCG immunotherapy in the bladder is the only input and concentration of BCG in effector cell is only measured output then E = [1 0 0 0]T, and F = [0 1 0 0] The controllability and observability matrix are

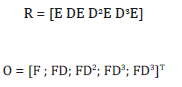
The rank of controllability and observability matrices is 1. The only measured output is affected cell due to cancer that we can easily measure. The system is not controllable and neither observable. The logistic model after substituting the dimensionless values, we get

The equilibrium points of (B, E, T_i, T_u) are (0.0701753, 1.70046, 1.48658, 139.033), (3, 5.56913×10⁻¹⁶, 4.39104×10⁻¹⁶, 0) and lies in the feasible region so the system is stable. In this case, the rank of controllability and observability matrices are 4 respectively. Hence the system is controllable and observable.

The mathematical analysis of Cancer model with nonlinear incidence has been presented. To observe the effects of the parameters using in this dynamics of Cancer model (1)-(4), conclude several numerical simulations varying the value of parameters given in Table 1 for source value and dimensionless values. Figure 1-4 shows by increasing the vaccination of immune system for logistic model according to dimensionless values, effecter cells and total population of affected cells become stable while total population of unaffected cells increases efficiently.

Table 1:Table of parameters values used in the model.

Figure 1:Numerical simulation of logistic model with dimensionless values.

Figure 2:Numerical simulation of logistic model with dimensionless values.

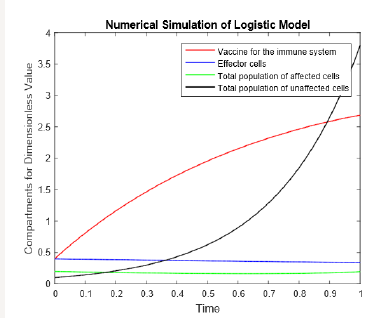
Figure 3:Numerical simulation of logistic model with dimensionless values.

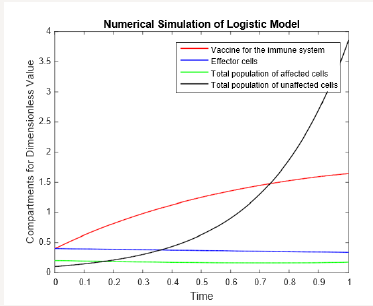
Figure 4:Numerical simulation of logistic model with dimensionless values.

We find the linear control of the model because if the linear system is controllable and observable then nonlinear system may or may not be controllable and observable. Model consist two categories according to parameter values i.e source and dimensionless values. For dimensionless values of the parameters, we have two equilibrium points in which system has solution in the feasible region. Model is controllable and observable for first equilibrium point but for second equilibrium point model is partially controllable and observable. Numerical simulations reveals that the logistic model give better impact with BCG vaccination strategies. We observe that BCG has a very positive impact to control cancer at the initial level.

1. Aggarwal SK, Carter GT, Sullivan MD, Zum Brunnen C, Morrill R, et al. (2009) Medicinal use of cannabis in the United States: Historical perspectives, current trends, and future directions. J Opioid Manag 5(3): 153-168.
2. French M (2014) Moms, marijuana-for-kids campaign seeks to quiet epilepsy.
3. Gloss D, Vickrey B (2014) Cannabinoids for epilepsy. Cochrane Database Syst Rev (3): CD009270.
4. Anderson A, Chaplain M (1998) Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Biol 60(5): 857-899.
5. Piccoli B, Sussmann HJ (2000) Regular synthesis and sufficiency conditions for optimality. SIAM J Control Optimization 39(2): 359-410.
6. Castiglione F, Piccoli B (2007) Cancer immunotherapy, mathematical modeling and optimal control. Journal of Theoretical Biology 247(4): 723-732.
7. Coron JM (2007) Control and nonlinearity. American Mathematical Society 136: 1-444.
8. Camlibel MK, Heemels H (2007) Controllability of linear systems with input and state constraints, Proceedings of the 46th IEEE Conference on Decision and Control New Orleans, LA, USA, pp. 1-6.
9. Saleem MU, Farman M, Ahmad MO, Rizwan M (2017) Control of an artificial human pancreas. Chinese Journal of Physics 55(6): 2273-2282.
10. Saleem MU, Farman M, Ahmad A, Meraj MA (2018) Mathematical model based assessment of the cancer control by Chemo-Immunotherapy. Pure and Applied Biology 7(2): 678-683.