Multilayer Viscoelastic Media with Interface Quality Using Pseudo Stroh-Formalism: Application to Local Materials

Introduction

Laminated structures have increased significantly because of their applications in the fields of aeronautics, aerospace and acoustics for noise reduction [1]. Several types of these structures have been studied among which we have double-glazing, perforated structures, and many others [2]. The approaches to study these structures are various: Impedance approaches, transfer matrix [3], Debye series decomposition method, and the stiffness matrix method [4]. These different approaches can be used to determine properties such as reflection, transmission, transmission loss and absorption. The attenuation and frequency shift of plate resonances have been studied for a supported structure with cavities [2]. They focused on the influence of the thickness of the layer containing the air and showed that, when the thickness of the layer containing the air is reduced, there is an increase in the attenuation in the system. Basten et al. [5] developed a model for double-glazing considering viscothermal effects in the air cavity. They showed that the attenuation of the plate modes could be increased by decreasing the thickness of the air layer. However, the influence of the viscothermal effects on the Sound Transmission Loss (STL) calculations is very slight in the considered frequency range (0-180 Hertz). Only around the clean frequencies of the panel, there are small differences between the results with and without viscothermal effects. Akrout et al. [6] studied the vibro-acoustic behaviour of double- laminated plates including the effects of viscosity and thermal conductivity of the cavity air. These results showed the importance of viscothermal effects in the case of perforated thin films containing air. Mu et al. [7] investigated the insulation performance of double and triple-glazed windows, showing that perforations in windows can prevent insulation degradation at resonance. They studied the STL of multilayer structures with a micro-perforated panel. In their work, they measured the STL using an impedance tube and a reverberation chamber and showed that using the transmission side of the multilayer structure effectively prevents the mass air resonance [8]. In addition, the works on the STL of multilayer structures without perforation are numerous among which, we have the study of the STL of light multilayer structures with thin air layers by Dijckmans et al. [9].

In this study, two models are presented: The first one is based on the transfer matrix and the second one is based on the vibroacoustic coupling between rooms, plates, and air cavities. Hyun-Sil Kim et al. [10] studied the STL of microperforated multilayer plates. A prediction model for the STL of multilayer microperforated plates is developed for plates with and without perforations. It is found that for low perforation ratios, the resonant frequencies of double and triple structures shift to high frequencies as these ratios increase. The study of the sound transmission of triple panel structures formed of poro-elastic materials using the transfer matrix was carried out by Liu [11]. Lee & Xu [12] developed a model based on the transfer matrix to determine the STL of multilayer materials including foams, leathers and rubbers. Similarly, Fu et al. [13] investigated the STL of laminated sandwich plate structures under sound wave excitation. Furthermore, Oliazadeh et al. [14] developed a statistical energy analysis model to evaluate the STL of honeycomb sandwich panels. Despite the numerous works on STL of perforated multilayer structures, to our knowledge, there is no study concerning the effect of the interface of the layers constituting the multilayer structure and the temperature. In addition, the application of our study to local materials made of Stabilized Earth Bricks (SEB) and Compressed Earth Bricks (CEB) for constructions in Cameroon has never been done. Indeed, the strength of a structure is closely related to the interface quality of the layers that constitute the structure and its cohesive properties. It is then necessary to investigate the influence of the adhesion quality between the layers constituting the multilayer structure. In this study, we propose to evaluate the influence of interface quality and temperature on the acoustic properties such as STL and absorption coefficient of the perforated multilayers. Despite the complexity of the problems to be studied, the PSF provides the 3D analytical solutions relatively simple and remains appropriate.

Problem Formulation

The stresses imposed by the wave motion in the thermoelastic multilayer structure are given by [15]:

The heat equation leads to the heat flow which is proportional to the temperature gradient.

where σ_ij, ε_kl and q_i are the mechanical stresses, strains and flows respectively. β_ij are the thermal stresses, k_ij is the thermal conductivity coefficient and T is the temperature. c_ijkl are the elastic moduli. The comma in Equation (2) indicates the differentiation relative to the x_j axis.

The equations of motion without volume force and thermal equilibrium are given by following [15]:

Heat conduction

The temperature variation for the simply supported structure can be written by [16]:

where

m and n two positive integers, and are two constants to be determined.

The components of the flux are obtained by combining Equation (4) and Equation (2) and we get:

Using Equations (4), (2) and (3), we obtain the following relationship:

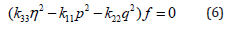
From Equations (5) and (6), we can write the relation:

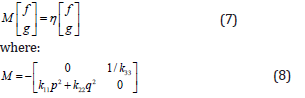
The general solution of the temperature-dependent propagation is obtained by using Equations (4) and (6) as follows:

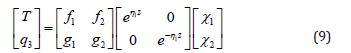
Where the column matrix x1 and x2 are to be determined. [f₁ g₁]^t and [f₂ g₂]^t are eigenvectors of Equation (7) which are independent.

Overall solutions

Simply supported multilayer structures admit the following expressions as solutions [17]:

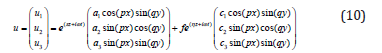
Substituting Equation (10) into Equation (3) and then into Equation (1) gives the tractions expressed as follows:

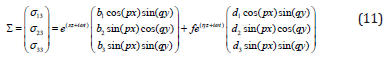
Where p=mπ/L_x and q=nπ/L_y, {m, n} are integers, {L_x, L_y} are the dimensions of the plate, the pulsation and t the time.

Fundamental matrix of pseudo-Stroh-formalism

The effective acoustic properties of the perforated polyethylene layer (PEp) are calculated according to Equation (12). The effective properties resulting from the induced proportion of air voids are deduced from the HS-ort homogenization model [18]. This approach, based on the model of Voigt is more adapted compared with the other approaches of homogenization, considering the shapes of holes induce in the perforated layer.

With ν the Poisson ratio and Vf the volume fraction.
The longitudinal velocities and elastic coefficients are related by:

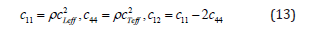
The eigenvectors b and d are respectively related to a and c as follows [17]:

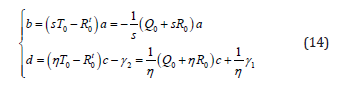
where Q₀, R₀, T₀ are three matrices defined by:

Combining Equations (10), (3) and (1), and substituting the result into Equation (4), we obtain the relationships below:

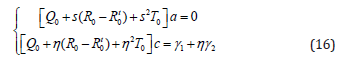
Using Equations (14) and (16), we can write:

where A is the fundamental matrix of Pseudo Stroh-formalism defined by:

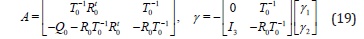
Equation (18) is an eigenvalue problem. It is solution in mechanics has been investigated by several authors [19,20]. In this study, we will use this formalism to determine the acoustic coefficients of multilayer structures. We will determine the transmission, sound transmission loss and absorption of thermoelastic multilayers with interface effect.

Propagation in a layer

The general solutions in layer j of a thermoelastic structure are obtained by superimposing Equations (10) and (5) given by the following relations [17]:

where K₁ and K₂ are column matrix to be determined.

With the interface conditions and the general solutions for each layer, the solution for the multilayer structure can be obtained [21]. Using Equation (9), the flux and temperature can be expressed for the layer j bounded by the surface z_j and z_j+1 as follows, with h_j the thickness of the layer:

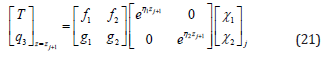
For z=z_j, Equation (9) leads to:

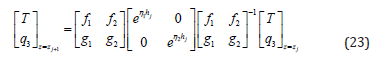
Combining Equations (21) and (22), the thermal variables of the lower and upper surfaces of layer j are related as follows:

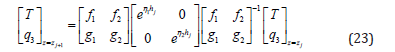
Moreover, when we replace the vectors and of Equation (22) in Equation (20), the elements of the column matrix are rewritten as:

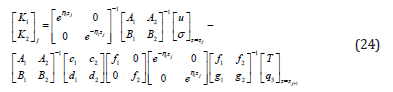
Combining Equations (20-24), we obtain the propagation relation from the upper to the lower interface of this structure:

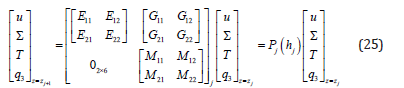
where P_j(h_j) is the propagation matrix in layer j of thickness hj, whose components are:

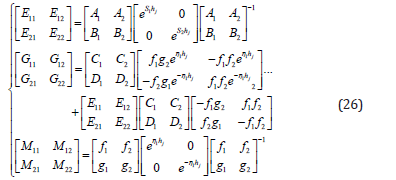
Imperfect interface

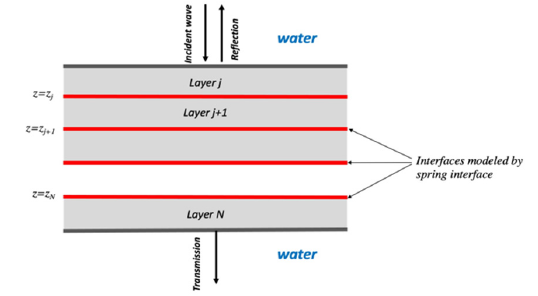
The geometry of our structure is shown in Figure 1. For this study, the linear model of the spring type was chosen to consider the imperfections due to the manufacturing and dislocation modes [15,22]. This model presents tensile continuity and displacement discontinuity for a mechanically imperfect interface. For a thermally imperfect interface, we have flow continuity and temperature discontinuity for a weakly conductive interface. On the other hand, if the interface is strongly conductive, there is temperature continuity and flow discontinuity [15]. The equations materializing the mechanically imperfect case represented by the continuity of tractions and discontinuity of displacements are written as [16]:

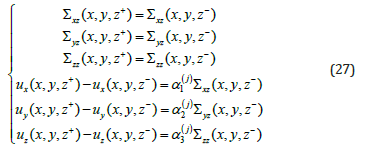
Figure 1:Multilayer structure with imperfect interface.

The constants

represent the slippage which depends on the stiffness of the spring. The perfectly bound case is given by

. In the case of a weakly conductive interface, the relations between flux and temperature are given by [16]:

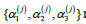
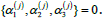
where β_T^(j) is the constant that depends on the material. β_T^(j)=0 corresponds to the case of perfect interface. On the other hand, when the interface is strongly conductive, we have:.

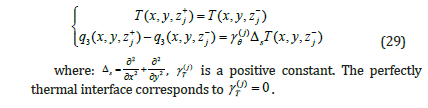
Thermomechanical interface matrix

In this section, the mechanically imperfect and thermally conductive interfaces are presented. The combination of Equation (27) and (28) leads to the equation below:

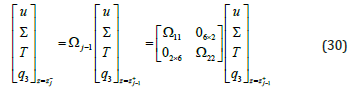
z⁺ and j z⁻ represent respectively the upper and lower surfaces of the layer j.

For a weakly conductive interface, the matrices Ω₁₁ and Ω₂₂ are given as a function of mechanical and thermal parameters:

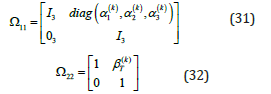
However, when the interface is highly conductive, we have:

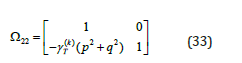
The components of displacements, tractions, temperatures and fluxes of the upper surface of layer j are related to those of the lower surface of the latter with imperfect interface by the relation.

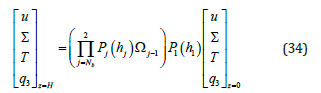
N_b is the total number of layers. The previous relationship (Equation (34)) is unstable at high frequencies. To overcome these instability problems, we use the Dual Variable and Position (DVP) method [23]. For this, we rewrite Equation (34) as:

For easy handling, we adopt the notations uT and tq and Equation (35) becomes:

Acoustic coefficients of the structure

The flexibility matrix extracted from Equation (39), allows us to calculate the acoustic coefficients given by [17]:

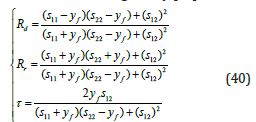
where s_ij =S_ij^N(3,3) and yf=cosφ/(jωZ_f), with φ the angle of incidence of the wave and Zf=ρfcf the acoustic impedance of the liquid in which the structure is placed. The coefficients R_d and R_r denoted the reflection coefficients as a function of the side of in sonification of the structure. However, whatever the side of insonification, the transmission does not change but the absorption differs depending on the side of insonification. The absorption coefficient is given by:

with α_d,r the absorption on the direct and reverse sides of the structure. The sound transmission loss (STL) is calculated from the transmission loss by the following relation:

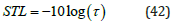
Numerical Results

The characteristics of layers constituting the period of the multilayer structure are given in Table 1. The density of the surrounding medium is equal to 1000 / ρ_P = kg m³ . The STL and absorption coefficients are presented in the frequency range between [0-1600] Hz.

Table 1:Characteristics of layers constituting the period of the multilayer structure.

Influence of the interface

As said previously, to describe an imperfect interface, the “mass-spring” model connecting the two layers in contact is used. It is principle consists of considering a continuity of strain and discontinuities of displacements. In this work, we have varied the spring stiffness between 0 to 4, with k₁=0 corresponding to the perfect interface and k₁=4 the case having poor interface quality. We assume that the structure is immersed in water and when the temperature is equal to zero water become an ice. Figure 2 shows the effect of interfaces parameters on STL of the AL/ PE structure without perforations. It is observed that the STL is strongly influenced by the variation of the interface parameter k₁ which determine the interface quality, between 100 and 600 Hz. We also observe a frequency shift toward small frequencies (Δf~70 Hz) and a decrease in amplitude (ΔAm~43%). When the interface parameter increases (i.e when the quality of interface is poor) a decrease in amplitude of STL is observed. In a range [0-100]Hz and [650-1000] Hz the STL is small insensitive to the variation of interface parameter.

Figure 2:Effect of interfaces conditions on STL of AL/PE periodic multilayer without perforations and temperature effects.

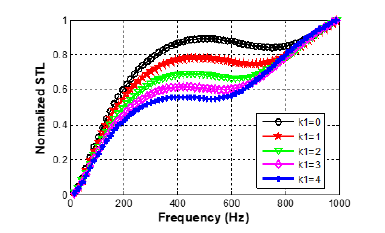
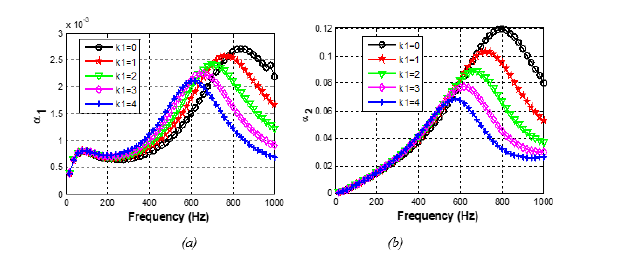
Considering the attenuation in the PE layer leads to a difference in absorption coefficient depending on the insonification side. Two absorption coefficients are obtained: absorption coefficient for the direct side (AL/PE) and absorption coefficient for the reverse side (PE/AL). It is observed that the AL/PE absorption coefficient contains two peaks, and the PE/AL absorption coefficient has only one peak (Figure 3). In addition, for both sides of insonification, the maximum peaks of the absorption curves shift towards lower frequencies when the interface parameter increases (i.e when the quality of interfaces is poor). The maximum frequency shift Δf~250 Hz. We also observed a decrease in amplitude (ΔAm~17% for AL/PE and ΔAm~44% for PE/AL). This demonstrates that the decrease in the interface quality leads to low-frequency absorption, therefore would induce errors when designing the structure. Pan et al. [15,17] have also showed this sensitivity of absorption coefficients depending on the spring stiffness for mechanical cases. It is also observed that, the maximum of absorption is reached when the interface parameter k₁=0, i.e when the interface is perfect. To consider the resin which is used to bond the AL/PE structure, it is important to play with interface parameter. Finally, by playing on the interface quality of the multilayer structure, it is quite possible to adjust the frequency position of the absorption peak, keeping the number of layers or periods. This is very important to know from the industrial point of view.

Figure 3:Effect of interfaces conditions on absorption coefficient of AL/PE (a) and (b) PE/AL periodic structure without perforation and temperature effects.

Influence of the temperature

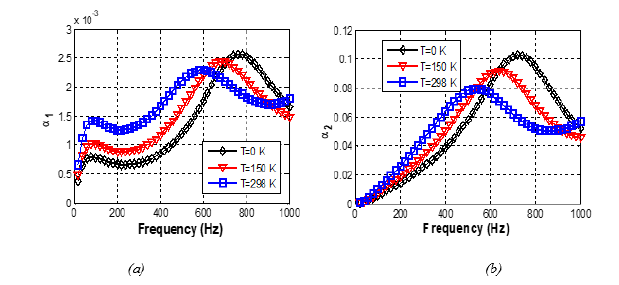
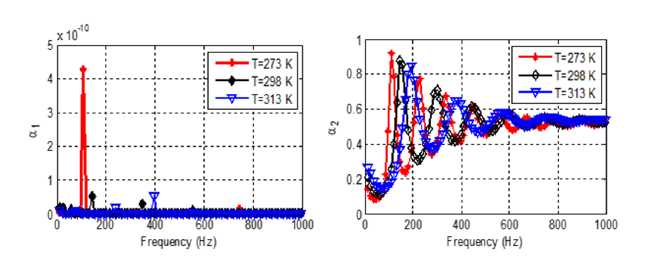
The influence of temperature on the acoustic properties of periodic multilayer structures is analysed. Figure 4 presents the STL obtained with and without temperature on a periodic multilayer of one period of AL/PE with k₁=1 and V_f= 0. The STL curves increase, starting at the same point (in zero) and reaching the maximum at 1000Hz. In the range between 200 and 600Hz, the curve with T=0 K is above the one with temperature and between 600Hz and 1000Hz, it is the curve at T=298K. This shows a difference between the acoustic properties of elastic materials and those of thermoelastic materials depending on frequency. This difference is observed in the STL amplitude. The summary of the different amplitudes is given in Table 2. Thus, the temperature reduces the amplitude of the STL when the frequency is lower than 600Hz and the peak observed at 400 Hz disappear. Figure 5 presents the case of the absorption coefficients. It clearly shows that the temperature produces a similar influence that interface quality: The frequencies shift of the maximum peaks of absorption toward smaller frequencies (Δf~170 Hz) and a decrease in amplitude of the maximum peak (ΔAm~12% for AL/PE and ΔAm~33% for PE/AL). This shift is the result of temperature heating and proves that when the material is heated, it becomes more supple and reaches its resonance peak faster. This result was also observed by Prasad et al. [24] on orthotropic materials where they showed that all acoustic coefficients are affected by temperature. These results could be very interesting to design absorbing multilayer structures in the low frequencies and able to be used in very high-temperature environments. Finally, both temperature and interface qualities produce similar influence on the absorption coefficients of the structure, but in the different proportions.

Figure 4:Effect of temperature on STL of a perfect AL/ PE periodic structure without perforation effects (V_f=0 and k₁=1).

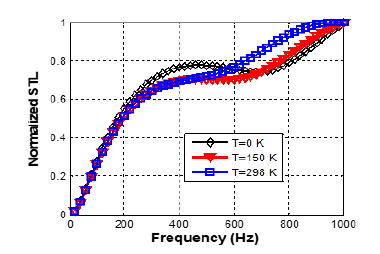
Table 2:Amplitude of STL for some frequencies.

Figure 5:Effect of temperature on the absorption coefficient of AL/PE with k₁=1 and V_f = 0: (a) direct and (b) reverse in sonification.

Influence of the perforations

In this section, the acoustic coefficients of the multilayer structure are calculated considering the Polyethylene perforated (noted PEp). The effective acoustic properties of the PEp are calculated according to the HS-ort homogenization model. The perforation evaluated in porosity rate estimated based on randomly drilled holes on the polymer layer and we consider room temperature condition i.e. T=298K. The evolution of STL according to the volume fraction of perforations is presented in Figure 6. This volume fraction varies between 10% and 50%. We observed that, between 300 and 800Hz, the amplitude of the sound transmission loss increases when the volume fraction increase. This result agrees with the study of Siryabe et al. [18] which observed the increase in the amplitude of the reflection coefficient when the volume fraction increase. The absorption coefficients are plotted as a function of insonification sides considering the volume fraction of perforations. As we can observe (Figure 7), an increase in the perforation rate in the structure induces a shift of the absorption peaks towards the lower frequencies on any part frequencies. These results were also obtained by Mu et al. [25] in their work on the influence of perforation on microperforated structures which shows that the absorption depends on the hole diameter and the perforation point.

Figure 6:STL as a function of frequency and volume fraction of perforation for AL/PE for k₁=1 and T=298K.

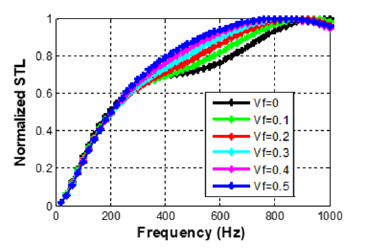
Figure 7:Absorption as a function of frequency and volume fraction for AL/PEp with k₁=1 and T=298 K: (a) direct and (b) reverse.

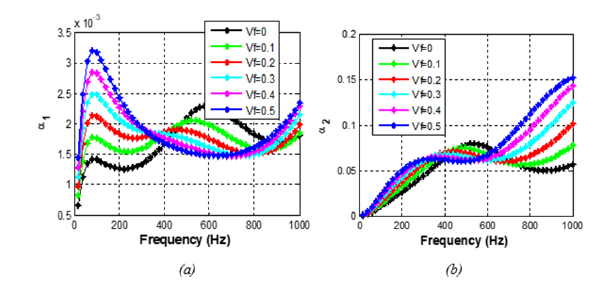
On both sides, we observe three intervals of variation according to the perforation rate. The first linear part goes from 0 to 100Hz in the direct side and from 0 to 300Hz to the reverse side. On this part, all the curves are straight lines and increase with the perforation rate. The range from 100Hz to 300Hz to the direct side shows a growth of the amplitude as a function of the volume fraction. The third part shows the fall of the absorption coefficient after the peak. In all these parts, we have a shift towards the lower frequencies and the maximum shift Δf~300 Hz. These results are in good agreement with those obtained by Toyoda et al. [26]. When the volume fraction is about 30% and more, the ripples multiply and we observe an evolving continuity of the ripples. Our results show that by playing with the volume fraction of the perforation, it is also quite possible to adjust the frequency position of the absorption peak, keeping the period or the number of layers.

Application to the local materials

The earth material is currently experiencing a revival of interest following the housing crisis because this material has many advantages in its current form for the construction of sustainable, comfortable and economic housing [27]. The earthen construction is a little bit everywhere in the world in general and in Cameroon in particular. This is related to the level of development of the inhabitants of each country in urban and rural areas because this construction technique is part of the cultural identity in Cameroon. Today, about 40% of the population lives in earthen houses. In this context, we analysed the acoustic behaviour of Stabilized Earth Bricks (SEB) and Compressed Earth Bricks (CEB). Figure 8 & 9 show respectively the STL and absorption coefficient. The structure is now placed in the air (c=343m/s). The ambient temperature is also considered (T=298K) and a volume fraction Vf=10% (this volume fraction is due to the presence of pores in earth bricks) is used. The elastic constants and thickness of the materials are presented in Table 3. As we can observed, the STL of SEB reaches its maximum at 200Hz and has three local minima at 15, 405 and 825Hz, respectively. The minimum for STL tends to 0.08. On the other hand, the STL of the CEB reaches its maximum at 175Hz and has four minima at 15, 330, 660 and 1000Hz. The minimum amplitude in this case tends to be 0.09. The SEB has a wider bandwidth than CEB and is therefore more suitable for noise reduction.

Figure 8:STL for stabilized (SEB) and compressed earth bricks (CEB) with k₁=0, V_f=10% and T=298 K.

Figure 9:Absorption spectra for stabilized (SEB) and compressed earth bricks (CEB) with k₁=0, V_f=10% and T=298 K.

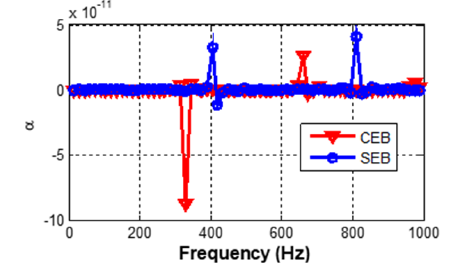
Table 3:Local materials properties.

The acoustic absorption curves of SEB and CEB are presented in Figure 10. The curves show one negative peaks for both curves: at 330Hz and 420Hz for CEB and SEB respectively. The positive part of SEB presents two peaks that reach their maximums at 400 and 800Hz. The CEB positive parts also show one peak at 660Hz. Finally, this result show that the SEB or CEB are very slight absorbing materials and in the next section, we will add to the SEB a layer of PE like a coating. In this application, we have k1=1, the volume fraction Vf=20%. Figure 11 presents the effect of temperature on the STL of the SEB/PE structure. The amplitude of the STL increases when the frequency increases and presents several minima. We observe an increase in the undulations which represent vibrations of the structure. These results show an increase in the bands which are observed on the curves in blue which corresponds to the curve of T=313 K. We present in Figure 11 the absorption of multilayer structure. We observe a difference in the absorption curves according to the insonification side when considering the attenuation in the polyethylene layer. For the direct insonification, we observe a decrease of the amplitude peaks of absorption with temperature and frequency. At high temperature, these amplitudes tend to zero. In the reverse insonification case, a reduction of the amplitude when the frequency increases are also observed with a shift toward small frequencies.

Figure 10:Effect of temperature on STL of SEB/PE structure with k₁=1 and V_f=20%.

Figure 11:Absorption spectra for SEB/PE for direct and reverse with temperature variation.

Conclusion

This study presented the influence of the interface on the acoustic behaviour of perforated thermoelastic multilayers. We have developed the most widely used interface model, a linear model of the type of resort. This model provides information on the interaction of ultrasonic waves with the multilayer structure, whose interfaces have variable mechanical contact quality. Also, the influence of the volume fraction due to the presence of holes on the structure and the influence of temperature on the acoustic coefficients have been studied. The results showed that decreasing spring stiffness, which materializes the interface quality, the presence of perforations or temperature induced a shift in the position of the maximum absorption peak towards low frequencies. An application to local materials, such as SEB and CEB, was carried out and the results showed that temperature has a strong influence on the behaviour of these materials. Many of these materials exhibit low attenuation. When designing an acoustic absorber, it is important to consider the interface conditions, the thermal effect and the viscoelastic properties of the layers making up the multilayer structure.

References

1. Jamalpoor A, Savadkoohi AA, Hosseini M, Hosseini Hashemi S (2017) Free vibration and biaxial buckling analysis of double magneto-electro-elastic nanoplate-systems coupled by a visco-Pasternak medium via nonlocal elasticity theory. Eur J Mech A/Solids 63: 84-98.
2. Dijckmans A, Vermei G, Lauriks W (2010) Sound transmission through finite lightweight multilayered structures with thin air layers. Journal of the Acoustical Society of America 128(6): 3513-3524.
3. Hachemi M, Hamza-Cherif S (2020) Free vibration of composite laminated plate with complicated cut out. Mech Based Des Struct Mach 48(2): 192-216.
4. Vigran TE (2010) Sound transmission in multilayered structures Introducing finite structural connections in the transfer matrix method. Applied Acoustics 71(1): 39-44.
5. Basten TGHP, Van der Hoogt JM, Spiering RMEJ, Tijdeman H (2001) On the acousto-elastic behaviour of double-wall panels with a viscothermal air layer. Journal of Sound and Vibration 243(4): 699-719.
6. Kurra S (2012) Comparison of the models predicting sound insulation values of multilayered building elements. Applied Acoustics 73(6-7): 575-589.
7. Mu RL, Toyoda M, Takahashi D (2011) Improvement of sound insulation performance of multilayer windows by using microperforated panel. Acoust Sci Technol 32(2): 79-81.
8. Mu RL, Toyoda M, Takahashi D (2011) Sound insulation characteristics of multi-layer structures with a microperforated panel. Applied Acoustics 72(11): 849-855.
9. Dijckmans A, Vermeir G, Lauriks W (2010) Sound transmission through finite lightweight multilayered structures with thin air layers. Journal of the Acoustical Society of America 128(6): 3513-3524.
10. Hyun Sil K, Sang Ryul K, Bong Ki K, Pyung Sik M, Yun Ho S (2020) Sound transmission loss of multi-layered infinite micro-perforated plates. Journal of the Acoustical Society of America 147: 508-515.
11. Liu Y (2015) Sound transmission through triple-panel structures lined with poro elastic materials. Journal of Sound and Vibration 339: 376-395.
12. Lee CM, Xu Y (2009) A modified transfer matrix method for prediction of transmission loss of multilayer acoustic materials. Journal of Sound Vibration 326(1-2): 290-301.
13. Fu T, Chen Z, Yu H, Wang Z, Liu X (2018) An analytical study of sound transmission through stiffened double laminated composite sandwich plates. Aerosp Sci Technol 82: 92-104.
14. Oliazadeh P, Farshidianfar A, Crocker MJ (2022) Experimental study and analytical modeling of sound transmission through honeycomb sandwich panels using SEA method. Composite Structure 280: 114927.
15. Vattré A, Pan E (2020) Thermoelasticity of multilayered plates with imperfect interfaces. International Journal of Engineering Science 158: 1-30.
16. Wang X, Pan E (2007) Exact solutions for simply supported and multilayered piezothermo-elastic plates with imperfect interfaces. Open Mechanics Journal 1: 1-10.
17. Chen J, Guo J, Pan E (2017) Reflection and transmission of plane wave in multilayered nonlocal magneto-electro-elastic plates immersed in liquid, Composites Structures 162: 401-410.
18. Siryabe E, Ntamack GE, Marechal P (2013) Holes effects in plane periodic multilayered viscoelastic media. Open Journal of Acoustics 3(3): 80-87.
19. Pan E, Han F (2005) Exact solution for functionally graded and layered magneto-electro-elastic plates. International Journal of Engineering Science 43(3-4): 321-339.
20. Ewolo Ngak FP, Ntamack GE, Azrar L (2019) Dynamic analysis of multilayered magneto electro elastic plates based on the pseudo-Stroh formalism and lagrange polynomials. Journal of Intelligent Material Systems and Structures 30(6): 939-962.
21. Manyo Manyo JA, Ntamack GE, Azrar L (2021) 3D-dynamic modeling of cross-ply magneto-electro-elastic laminates based on the pseudo-Stroh formalism. Mechanics of Advanced Materials and Structures 28(13): 1337-1354.
22. Fan H, Wang G (2003) Screw dislocation interacting with imperfect interface. Mech Mater 35(10): 943-953.
23. Manyo Manyo JA, Ntamack GE, Azrar L (2022) Time and frequency 3D-dynamic analyses of multilayered magneto electro elastic plates with imperfect interfaces. Archive of Applied Mechanics 92: 2273-2301.
24. Prasad B, Kundu S, Chandra Pal P (2019) Impact of initial stress on reflection and transmission of SV-wave between two orthotropic thermoelastic half-spaces. Journal of Solid Mechanics 11(4): 778-789.
25. Mu RL, Toyoda M, Takahashi D (2011) Sound insulation characteristics of multi-layer structures with a microperforated panel, Applied Acoustics 72(11): 849-855.
26. Toyoda M, Takahasi D (2005) Reduction of acoustic radiation by impedance control with a perforated absorber system. Journal of Sound and Vibration 286(3): 601-614.
27. Goutsaya J, Ntamack GE, Kenmeugne B, Charif DOS (2021) Mechanical characteristics of compressed earth blocks, compressed stabilized earth blocks and stabilized adobe bricks with cement in the town of Ngaoundere-Cameroun. Journal of Building Materials and Structures 8: 139-159.