Determination of Thermodynamic Parameters Related to Micro-Simulation in Friction Stir Welding of Dissimilar Al/Mg Alloys

In the context of energy conservation and emission reduction, lightweight structures have received more and more attention in manufacturing transportation vehicles. As the most common lightweight alloys, aluminum and magnesium alloys have been widely used in aviation, aerospace, transportation and other industries [1,2]. The hybrid components of aluminum/magnesium alloys can make the advantages of the two materials complement each other and realize cross application. Therefore, the efficient joining of aluminum/magnesium alloys is of great application potential. As a solid-state welding process, Friction Stir Welding (FSW) has great advantages in joining dissimilar Al/Mg alloys due to its low heat input, little distortion and few defects [3]. However, studies have shown that brittle and hard Intermetallic Compounds (IMCs) still exist in FSW joints of dissimilar Al/Mg alloys, which affect the mechanical properties of the joints. Many scholars have conducted the experimental characterization of IMCs generated during FSW of Al/Mg alloys [4-6], but only the IMCs in the final weld can be observed and characterized. Up to now, there is no in-situ characterization method to reveal the formation and growth mechanism of IMCs. Numerical simulation is a powerful means of studying such problems. By establishing a model, the formation and growth of IMCs can be predicted, which can save a lot of experimental costs and provide a theoretical basis for the regulation of IMCs. However, it is the premise of establishing the IMCs model to know the relevant microscopic thermodynamic parameters, among which the most important ones are the Gibbs free energy density of the generated phases and the interface energy of the heterogeneous phases [7,8].

The density of Gibbs free energy of each phase in the FSW process of Al/Mg alloys determines the direction of microstructure evolution, because the decrease of Gibbs free energy density is the most important driving force for the growth of heterogeneous phases. To simulate the growth of IMCs in the FSW process of Al/ Mg alloys, the expression of Gibbs free energy density of each phase with concentration and temperature is required. Previously, the Gibbs free energy density model of Al-Mg system was obtained by calculating the phase diagram based on the experimental results. To solve the problem that the solid solubility of Mg in Al is too large in the previous phase diagram calculation model, Saunders [9] introduced the sub-lattice model parameters of the intermediate phase and proposed a more accurate calculation phase diagram model. Zuo et al. [10] proposed a Gibbs free energy density model of Al-Mg system with fewer parameters and obtained better fitting results compared with the experiments. However, the early method of calculating the phase diagram involves too many thermodynamic parameters and the calculation steps are cumbersome, which limits its application in computer simulation of IMCs. With the development of computers, the thermodynamic properties of materials have been integrated into the CALPHAD database [11] and the thermodynamic data of related phases can be extracted according to the working conditions. Using the thermodynamic database, it is very convenient to calculate the Gibbs free energy density of each phase at a certain concentration or a certain temperature, and then a formula is used to fit the data. For the Gibbs free energy density curve at a certain temperature, the most common fitting method is polynomial fitting [12,13]. The FSW process is a temperaturevarying process, and the common isothermal fitting method cannot be applied. Therefore, it is necessary to use the thermodynamic database to fit the expression of the Gibbs free energy density of each generated phase with temperature and concentration for the temperature-varying process. However, for the Al-Mg system, there is no simple and effective expression for the Gibbs free energy density suitable for the variable temperature process.

Another challenge to simulate the growth of IMCs in the FSW process of Al/Mg alloys is the uncertainty of the interfacial energy at the interface of heterogeneous phases. Due to the difficulty of the relevant experimental measurement, there is little information on the measured values of the heterogeneous interface energy of the Al-Mg system. With the emergence of various smallscale computational models and the development of computer technology, Molecular Dynamics (MD) method has become a powerful tool to study heterogeneous interface energy. Yang et al. [14] used MD method to study the effect of orientation mismatch on the interface strength of Au biocrystals with different grain orientations. Hu et al. [15] calculated the liquid-solid interface energy of uranium metal by two MD methods, i.e., the critical nucleation method and the capillary wave method. It was found that the calculation results of the two methods were not much different, and the results were in good agreement with the experimental ones. Sun et al. [16] obtained the solid-liquid interface energy of HCP-Mg by MD method and calculated the anisotropy of the crystal. In this work, the CALPHAD database was used to obtain the Gibbs free energy density of FCC-Al, Al₃Mg₂, Al₁₂Mg₁₇ and HCP-Mg at different temperatures and concentrations. A simple and effective expression of the Gibbs free energy density suitable for the temperature range in the FSW process was obtained by polynomial fitting of the data. The heterogeneous interface energy of Al-Al₃Mg₂ and Mg-Al₁₂Mg₁₇ was calculated by molecular dynamics method. The determination of such parameters provided data basis for the simulation and prediction of IMCs growth in FSW process of Al/Mg alloys.

Function fitting of Gibbs free energy density

To obtain the expression of the Gibbs free energy density with two variables of concentration and temperature, the CALPHAD database of Thermo-calc software was used to calculate the Gibbs free energy density of the four phases (Al, Al₃Mg₂ and Mg-Al₁₂Mg₁₇, Mg). Firstly, Extract Gibbs free energy density data of four phases under isothermal conditions between 20 °C and 540 °C at an interval of 40 °C from the database, and then fit them using a quartic polynomial. After that, the change of fitting parameters with temperature was observed, and the fitting parameters were constructed as a function of temperature. Finally, the fitting parameters were brought into the polynomial to obtain the expression of Gibbs free energy density

Fitting solutions: The phase diagram of Al-Mg system is shown in Figure 1. It can be seen from the phase diagram that Al, Al₁₂Mg₁₇ and Mg have a certain composition range, while the composition range of Al₃Mg₂ is very narrow, which is shown as a point in the Gibbs free energy density diagram. However, sometimes the derivative term of Gibbs free energy density is needed in the numerical simulation. Thus, the following fitting scheme is adopted: Under isothermal conditions, the Gibbs free energy density of Al, Al₁₂Mg₁₇ and Mg phases is fitted by quartic polynomial. Because Al₃Mg₂ is a point in the Gibbs free energy density diagram, the quadratic function is used to fit it. The vertex of the function is the corresponding point in the free energy density diagram, and the coefficient of the quadratic term is taken. The value makes the opening of the quadratic function very narrow to meet the conditions of the narrow composition range of Al₃Mg₂. The fitting formulas are as follows:

Figure 1:Al-Mg binary phase diagram.

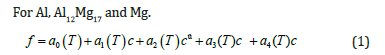
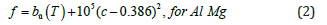
where a₀(T), a₁(T), a₂(T), a₃(T) and a₄(T) are the fitting coefficients that change with temperature and f is the free energy density of the corresponding phase.

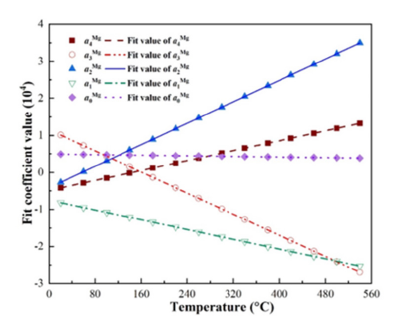
Function fitting of undetermined coefficients with temperature: In the previous section, the free energy density of the four phases under isothermal conditions was fitted in the form of a quartic function, resulting in five fitting parameters varying with temperature. To determine the variation of the five fitting parameters with temperature, the Gibbs free energy density between 20 °C and 540 °C at intervals of 40 °C was calculated respectively. It was found that the fitting parameters showed a linear relationship with the change of temperature. The change of fitting parameters with temperature and the fitting curve are shown in Figures 2-5. It can be seen from the figures that the fitting coefficients of the four phases change linearly with temperature. The expression of the fitting coefficients of each phase can be obtained by linear fitting, and it is brought into the expression of free energy density. The results are as follows:

Figure 2:Change of fitting coefficients of Al with temperature.

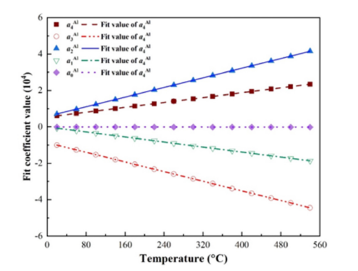
Figure 3:Change of fitting coefficients of Al₃Mg₂ with temperature.

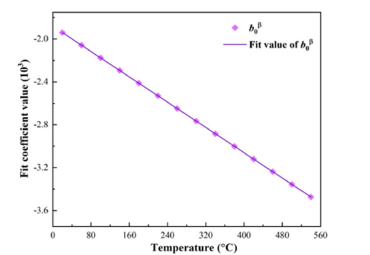
Figure 4:Change of fitting coefficients of Al₁₂Mg₁₇ with temperature.

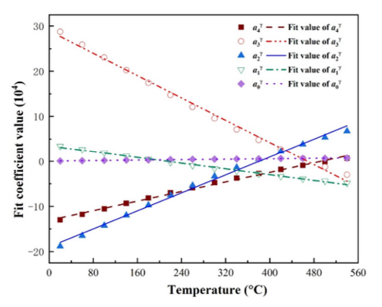
Figure 5:Change of fitting coefficients of Mg with temperature.

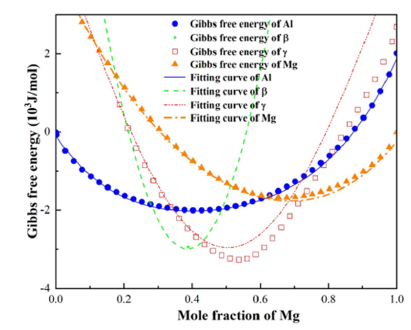
Verification of free energy density fitting effect: To verify whether the fitted expression can accurately predict the free energy density of each phase, the fitting values of free energy at 360 °C (the peak temperature of FSW process of Al/Mg alloys [17]) were selected to compare with the calculated values of CALPHAD database. The comparison results are shown in Figure 6. It can be seen from the figure that the three phases of Al, Al3Mg2 and Mg can be consistent with the values of CALPHAD database, while the Al₁₂Mg₁₇ phase has a slight error. The larger the Mg atom concentration is, the larger the fitting error is. The correlation coefficients were all above 0.95, indicating that the predicted value was strongly correlated with the value of CALPHAD database. In the simulation, the commonly used concentration range of Al₁₂Mg₁₇ phase is about 0.586. In this range, the linear fitting undetermined coefficients have reached a smaller error range, and the linear relationship is easier to program and calculate. Therefore, the expressions (3), (4), (5) and (6) can be used as the fitting expressions of the Gibbs free energy density.

Figure 6:Change of fitting coefficients of Mg with temperature.

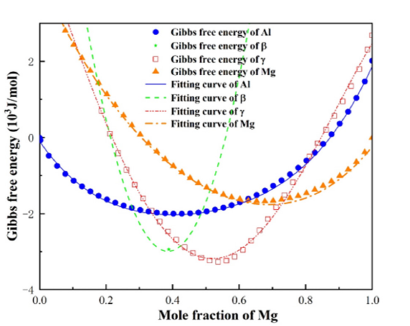
If some work requires high precision, the above Al₁₂Mg₁₇ phase can also be fitted with higher precision: the quadratic polynomial is used to fit the change of the undetermined coefficients with temperature. After quadratic expression fitting, the comparison between the fitting values and the values of CALPHAD database are shown in Figure 7. It can be seen from the figure that the prediction accuracy of Al₁₂Mg₁₇ is improved by using the quadratic fitting undetermined coefficients, and the predicted values are basically consistent with the calculated values of CALPHAD database. However, the quadratic fitting will bring more calculation. Workers can choose according to the actual situation. The function after quadratic fitting is:

Figure 7:Comparison of predicted and experimental values using quadratic fitting undetermined coefficients.

Molecular dynamics simulation interface energy

The molecular dynamics method is used to calculate the heterogeneous interface energy of Al-Mg system, which is an important factor affecting the growth of IMCs.

Force field: The Al-Mg system is an alloy system, and the commonly used potential function is the embedded atom potential (EAM potential). The core idea is that the nucleus of an atom is not only affected by the interaction of other nucleus around it, but also by the background electron cloud generated by the electrons outside the nucleus and the electrons outside the nucleus of other atoms around it. The total potential energy of atom i is written as:

On the right-hand side of Eq. (8), the first term is the two-body potential part, which reflects the pair interaction between i and j atoms. The second term is embedding energy, which represents the energy generated by the presence of electron density when the i atom is embedded in the matrix with electron density of ρi. In this work, the EAM potential of Al-Mg system proposed by Mendelev et al. [18] is used to simulate the interaction between Al and Mg atoms.

MD simulation method: To establish the MD model, the crystal structures of Al, Al₃Mg₂, Al₁₂Mg₁₇ and Mg were extracted from the ICSD database, as shown in Figure 8. However, the extracted crystal structure cannot be directly used to establish the interface model, and the interface relationship between different phases must be satisfied [19,20]:

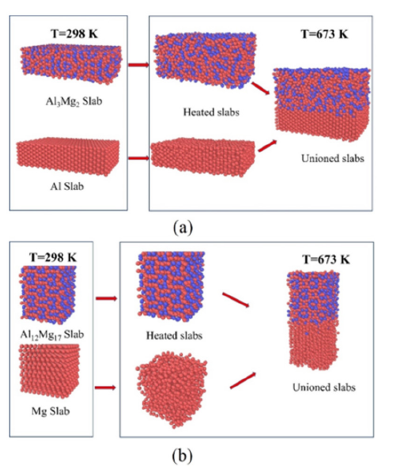
After the crystal structure is introduced, the heterogeneous interface is oriented to the corresponding coherent interface through sectioning and copying. At room temperature (298K), the Al and Al₃Mg₂ blocks of 50Å×70Å×25Å and the Mg and Al₁₂Mg₁₇ blocks of 32Å×30Å×67Å were established. After that, it was heated to a high temperature at a heating rate of 0.1K/fs, and then relaxed for 10fs at high temperature to extract the energy of the two blocks respectively. Finally, the two are combined. After the two are combined, an interface will be formed and the total energy was extracted after the interface was formed. The interface energy can be calculated according to the change of energy in the process, and the whole process is shown in Figure 9.

Figure 8:Crystal structure of (a) Al, (b) Al₃Mg₂, (c) Al₁₂Mg₁₇ and (d) Mg.

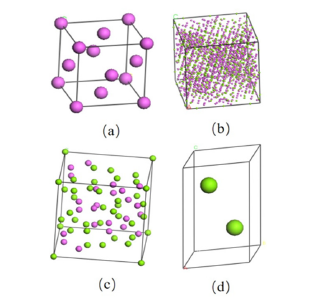
Figure 9:The interface energy calculation process of (a) Al and β phase and (b) Mg and γ phase.

After calculating the energy change of the system, the interface energy can be calculated according to the formula:

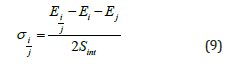
where S_int is the area of the bonding interface, Ei/j is the total energy of the combined system, E_i and E_j are the energy of the two independent subsystems.

Simulation result: Molecular dynamics simulation was performed using LAMMPS software [21]. Firstly, use Materials Studio software to geometrically model the heterogeneous interface and obtain input files for atomic species, mass, and position. Then, it is imported into the LAMMPS solver, where ensemble, temperature, boundary conditions, and relaxation time are inputted. Finally, output quantities such as atomic trajectories and system energy are obtained. The Open Visualization Tool (OVITO) [22] was used to visualize the atoms and their positions. The periodic boundary conditions were used in the x and y directions, and the non-periodic boundary conditions were used in the z direction. The temperature of the system was controlled by regular ensemble (NVT). The velocity-Verlet algorithm was used to solve the Newton ‘s motion equation for each time step. The time step was 1fs.

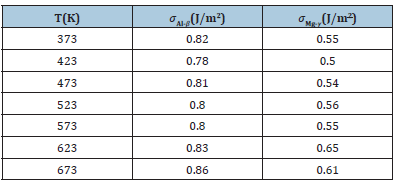
The interface energies of Al-Al₃Mg₂ and Al₁₂Mg₁₇-Mg in the temperature range of 373K-673K were calculated. In the process of extraction, the energy of the four phases alone and after the formation of the bonding interface is shown in Table 1. It can be seen from Table 1 that the total energy after bonding is slightly lower than the total energy of the two separate blocks, because the surface energy of the original contact surface disappears after the interface is formed. The interface energy obtained by the formula (9) is shown in Table 2. It can be seen from Table 2 that the heterogeneous interface energy does not change drastically with temperature. The calculated interfacial energy of Al-Al₃Mg₂ and Al₁₂Mg₁₇-Mg is 0.82J/m2 and0.58 J/m2, respectively.

Table 1:Total energy of each system at different temperatures.

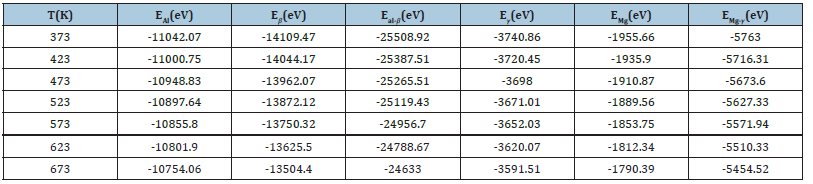
Table 2:The heterogeneous interface energy at different temperatures.

A. The free energy density of each phase in Al-Mg system was poly nominally fitted at different temperatures by using the data in the CALPHAD database. The relationship between the fitting coefficients and temperature was established, and it was found that the fitting coefficient was linear with temperature. The expressions of Gibbs free energy density of Al-Mg system with concentration and temperature were established. Compared with the results of CALPHAD database, the fitting formula can accurately predict the Gibbs free energy density of each phase at different temperatures and concentrations.
B. The calculation model of heterogeneous interface energy was established by molecular dynamics method. The interface energy of Al-Al₃Mg₂ and Al₁₂Mg₁₇-Mg at different temperatures was calculated.
C. The data calculated in this work can be used in the modeling of IMCs prediction. The proposed expressions are simple but effective, which lays a foundation for the computer simulation of IMCs growth in dissimilar FSW of Al/Mg alloys.

The authors acknowledge the financial support from the Key R & D Program of Shandong Province in China (Grant No. 2021ZLGX01).

1. Varmazyar J, Khodaei M (2019) Diffusion bonding of aluminum-magnesium using cold rolled copper interlayer. J Alloys Compd 773: 838-843.
2. Zhang T, Wang W, Zhang W, Wei Y, Cao X, et al. (2018) Microstructure evolution and mechanical properties of an AA6061/AZ31B alloy plate fabricated by explosive welding. J Alloys Compd 735: 1759-1768.
3. Schmidt H, Hattel J (2005) A local model for thermomechanical conditions in friction stir welding. Modell Simul Mater Sci Eng 13(1): 77-93.
4. Yamamoto N, Liao J, Watanabe S, Nakata K (2009) Effect of intermetallic compound layer on tensile strength of dissimilar friction-stir weld of a high strength mg alloy and al alloy. Mater Trans 50(12): 2833-2838.
5. Firouzdor V, Kou S (2010) Formation of liquid and intermetallic in Al-to-Mg friction stir welding. Metall Mater Trans A 41: 3238-3251.
6. Otmar Klag JG, Guntram Wagner, Rainer S Fetzer, Dietmar Eifler (2014) Microstructural and thermodynamic investigations on friction stir welded Mg-Al joints. Int J Mater Res105(2): 145-155.
7. Kunwar A, Yousefi E, Zuo X, Sun Y, Seveno D, et al. (2022) Multi-phase field simulation of Al₃Ni₂ intermetallic growth at liquid Al/solid Ni interface using MD computed interfacial energies. Int J Mech Sci 215: 106930.
8. Aagesen LK, Schwen D, Ahmed K, Tonks MR (2017) Quantifying elastic energy effects on interfacial energy in the Kim-Kim-Suzuki phase-field model with different interpolation schemes. Comput Mater Sci 140: 10-21.
9. Saunders N (1990) A review and thermodynamic assessment of the Al-P and Mg-Li systems. Calphad 14(1): 61-70.
10. Zuo Y, Chang YA (1993) Thermodynamic calculation of the AI-Mg phase diagram. Calphad 17(2): 161-174.
11. Kubendran Amos PG, Schoof E, Schneider D, Nestler B (2018) Chemo-elastic phase-field simulation of the cooperative growth of mutually accommodating Widmanstätten plates. J Alloys Compd 767: 1141-1154.
12. Attari V, Arroyave R (2016) Phase field modeling of joint formation during isothermal solidification in 3DIC Micro packaging. J Phase Equilib Diffus 37: 469-480.
13. Kunwar A, Hektor J, Nomoto S, Coutinho YA, Moelans N (2020) Combining multi-phase field simulation with neural network analysis to unravel thermomigration accelerated growth behavior of Cu₆Sn₅ IMC at cold side Cu-Sn interface. J Mech Sci 184: 105843.
14. Yang Z, Lian J, Wang J (2013) Molecular dynamics simulation of thin film interfacial strength dependency on lattice mismatch. Thin Solid Films 537: 190-197.
15. Hu G, Luo C, Wu L, Tang Q, Ren Z, et al. (2020) Molecular dynamics simulation of solid/liquid interfacial energy of uranium. J Nucl Mater 538: 152183.
16. Sun DY, Mendelev MI, Becker CA, Kudin K, Haxhimali T, et al. (2006) Crystal-melt interfacial free energies in hcp metals: A molecular dynamics study of Mg. Phys Rev B 73(2): 024116.
17. Yang CL, Wu CS, Lv XQ (2018) Numerical analysis of mass transfer and material mixing in friction stir welding of aluminum/magnesium alloys. Journal of Manufacturing Processes 32: 380-394.
18. Mendelev MI, Asta M, Rahman MJ, Hoyt JJ (2009) Development of interatomic potentials appropriate for simulation of solid-liquid interface properties in Al-Mg alloys. Philos Mag 89(34-36): 3269-3285.
19. Zhao Y, Ding Z, Chen Y (2017) Crystallographic orientations of intermetallic compounds of a multi-pass friction stir processed Al/Mg composite materials. Mater Charact 128: 156-164.
20. Zhou JP, Zhao DS, Wang RH, Sun ZF, Wang JB, et al. (2007) In situ observation of ageing process and new morphologies of continuous precipitates in AZ91 magnesium alloy. Mater Lett 61(25): 4707-4710.
21. Steve P (1995) Fast parallel algorithms for short-range molecular dynamics. J Comput Phys 117(1): 1-19.
22. Stukowski A (2010) Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Modell Simul Mater Sci Eng 18: 015012.