Materials Selection for Malleable Cast-Iron Pipe Fittings with a Numerical Method

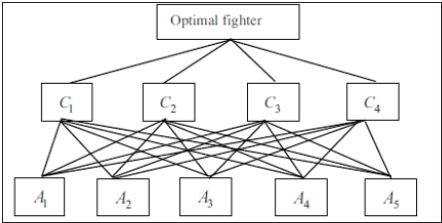
White cast iron is annealed to produce malleable cast Iron with granular graphite in ferrite or perlite matrix depends on chemical composition and heat treatment [1]. Importance of malleable cast irons selection comes from their low manufacturing cost and machining ability. Pipe fittings are the main application of these types of materials in vehicles, oil and petrochemical, mining, iron and steel, agricultural and electrical industries [2]. Nowadays, threaded fittings as oldest methods of joint in piping systems made by malleable cast irons. their properties such as strength, machining ability, erosion and corrosion resistance will enhance by specific heat treatments [3]. Using the mathematical logic is highly necessary when we faced with several criteria in selection. Analytical Hierarchical Process (AHP) is a decisionmaking technique for ranking the solutions and select their best. This procedure was always a frequently used method in most of the decision-making problems [4]. As indicated in Figure 1, the criteria and the alternatives with regards to the target are housed in a hierarchical tree [5]. In other word, a complex problem breaks down into a simple structure.

Figure 1:Hierarchical structure for selection the proper alternative [4].

As long ago, there are many studies conducted over the mathematical models in materials selection. Roy et al. [5], revealed that it possible to achieve the optimal parameters in sub-merge weld joint of plain carbon steel using AHP model in the absence of microstructure characterization. Chakladar et al. [6], also presented a new hybrid model of AHP and TOPSIS to rank the metal machining parameters. The TOPSIS method is another decisionmaking method in alternative selection using the similarity of each alternative to ideal solution. In this method, there is a requirement to calculating the relative weight of criteria by the mean of additional models such as AHP [7]. In this study, the most proper alternative for pipefitting was selected out of five most used malleable cast iron by the means of the presented model with respect to six criteria: melt fluidity, solidification shrinkage, machining ability, yield strength and Ultimate Strength (UTS).

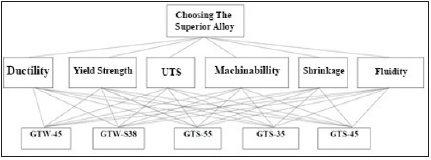
The selected materials for case study consist of five different malleable cast iron that presented in Table 1. Casting and machining are the essential step in pipe-fitting fabrication [3]. Hence the characteristics affecting those processes are chosen as problem criteria and considered by AHP and TOPSIS models. Dependence of alternatives to criteria for selecting the best alternative is shown in Figure 2. The GTS-55 has been reported as best malleable cast iron by investigating the interactions between criteria based on AHP and TOPSIS and comparing with practical situation. Analyses of results will be discussed as follows.

Table 1: The alloys properties of case study [15].

Figure 2: The hierarchy of criteria and alternatives in respect to objective.

Determination of criteria priority by AHP

As said earlier, the objective of this research is selecting the malleable cast iron for pipe fitting with respect to properties related to mainly mechanical properties. Therefore, the melt fluidity, solidification shrinkage, machining ability, yield strength and Ultimate Strength (UTS) have been chosen to achieve these properties. The procedure of scoring is provided in Table 2 based on pair-wise comparisons. By the using of data achieved from Table 1 & 2, the selected criteria were compared with each other and finally weights have been assigned. Calculating the weights depends on innate properties of materials and other parameters like melt pouring temperature, cooling rate and etc have been discarded in this paper.

Table 2: Numerical scale for weight scoring and relative importance of criteria and options relative to each other in the pairwise judgment matrix based on 1 to 9 values [8,16].

Analytic Hierarchy Process (AHP) first has introduced by Saaty in 1980 [8]. The AHP approach was designed to incorporate qualitative and quantitative aspects of a complex problem with multiple criteria and solves them by decomposing the problem into hierarchies and the Decision Maker (DM) then make Pair Wise Comparison (PWC) judgments of criteria as to importance of priorities in each hierarch [9]. A fundamental problem in decisionmaking is to grade the importance of a set of alternative and assign a weight to each of them. The importance of alternative usually depends on several criteria which can be evaluated within the PWC. Disadvantages of AHP make Saaty and other researcher to improve the model with regard to the effect of the criteria on each other [8].

Hierarchy should be approved by decision making team at the first step and the decision-making matrix provided in the base on real data. Pair wise comparison carried out for criteria to obtains the relative importance of them. The result of comparison summarized in an n×n matrix (Equation 1). Decision matrix typically has quantitative values with different dimensions which have to be dimensionless in order to have ability in comparison and calculations using Equation 2. In pair-wise comparison matrix, the 9-point scoring is used by experts to prioritize the criteria (Table 2); [9,10]. The value of each criterion could be more or less than others. In this regard, if importance of the criterion A to criterion B stated as “a”, then the criterion B worth 1/a to criterion A. In the step ahead, pair-wise comparisons are carried out by experts and weights of criteria will be extracted and the final report summarized in a n×n matrix. it should be mentioned that the consistency of matrix must be validated which is prove the accuracy of judgment (Table 3);[11].

Table 3: Units and terms.

The Consistency Ratio (CR) of each Pair-wise comparison matrix (equation 3) let someone to know whether the comparisons are consistent or not. The CR calculated by Consistency Index (CI) that obtainable by equation 4 and Random Index (RI) which could be extracted from databases [12].

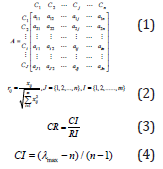
The upper limit of acceptance is 0.1 and if the CR exceed of this value then the procedure must be repeat [13]. In this model the Shannon entropy technique applied for calculating the weights [14].

TOPSIS Method

The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) which was first introduced by Yoon and Hwang [14] is the most common method to rank alternatives by criteria weights obtained by other method such as AHP. The basic concept of this method is that the selected alternative should have the shortest distance from the ideal solution and the farthest distance from the negative ideal solution [15,16]. The Euclidean distance approach was proposed to evaluate the relative closeness of the alternatives to the ideal solution [17].

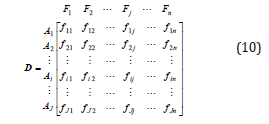
Decision matrix in Eq.10 typically has quantitative values with different dimensions which have to be dimensionless in order to have ability in comparison and calculations using Equation 11 [18].

Construct the weighted normalized decision matrix. With the set of weights, the weighted normalized matrix V can be generated as Eq. 12 [18].

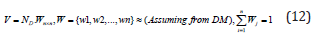
Determination the positive (A+) and negative (A-) ideal solutions by Eq 13 and Eq 14 respectively for benefit and cost criteria [18].

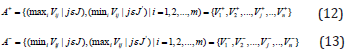
Calculating the separation measure form positive and negative points by Eq 15 and 16 respectively and calculating the relative closeness to the ideal solution and final ranking of alternatives using Eq 17 [18].

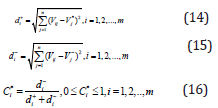
In the first instance, weights assigned to the alternatives according to criteria. Carbon equivalent of material is the main agent in fluidity. The closest carbon percent to the eutectic leads to raise the fluidity due to the diminution of mushy solicitation [16]. Besides, the shrinkage determinate by present of silicon. The higher the silicon, the lower the shrinkage [19]. The machinability is defined by hardness number, in such a way that the number reduces the machinability [1]. In the production of metallic joints, it is better to use a cast iron with higher yield and UTS strength [20]. Elongation obtained from tensile test shows alloy ductility (Tables 4-6).

Table 4: Pair comparison matrix criteria affecting cast iron selection.

Table 5: Normalization of pairwise comparison of effective criteria.

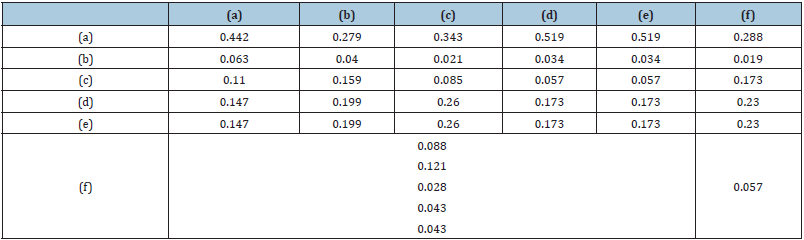
Table 6: Specified Weight for criteria in TOPSIS method.

Units and terms

Determining the priority of effective criteria on the selection of ideal Ductility of cast iron by AHP: The criteria for selecting the ideal hammer cast iron are determined by the experts and named in the following order:
a) Molten viscosity,
b) Shrinkage,
c) Machinability,
d) Yield strength,
e) Ultimate strength, and
f) Ductility.
Selecting ideal ductile cast iron by TOPSIS method: In TOPSIS method, Alternatives will be compared with each other. At the first stage, the decision matrix is formed consist of criteria in rows and alternatives in columns. It should be mentioned that the molten fluidity, yield strength, UTS strength and ductility are the positive criteria, and the shrinkage and hardness number are negative. Now the matrix 6 will be normalized using equation 11 and then will be weighted (Tables 7-12).
According to equation 13 to 14:
A*= {0.101,0.012,0.047,0.146,0.133,0.766} (17)
A-= {0.081,0.025,0.081,0.082,0.073,0.028} (18)

Table 7: Data of five types of cast iron used in pipe fittings.

By dividing the matrix values by the value obtained.

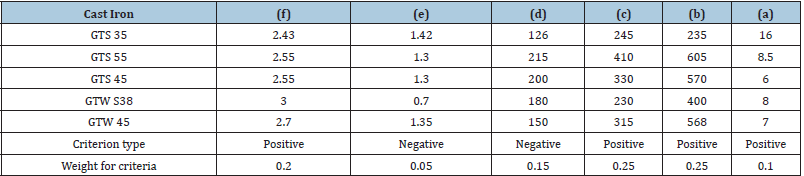
Table 8: The decision matrix normalization of five types of cast iron pipe fittings.

With the relative weight coefficient, the criteria in the normal matrix are.

Table 9: Weighting of the normalized decision matrix for five types of cast iron pipe fittings.

Table 10: Calculating the solution of positive and negative ideal.

Table 11: Calculate the size of the distance from the ideal positive and negative solution.

Table 12: Calculating the similarity to the ideal solution and ranking the alternatives.

To get the distance of each option from the ideal solution, the relation between equation 15 and 16 should be used:
S*= {0.030,0.023,0.049,0.097,0.075,0.083194} (19)
In the last step of Equation 17, the relative similarity to the ideal solution is calculated:
C*= {0.411,0.365,0.472,0.449,0.557,0.377} (20)
Nearest alternatives to 1, is introduced as most suitable alternative. Based on analyses, The GTS-55 has been selected as best material for pipe-joint.

In reference to conducted analysis and using the combination methods:

According to the calculations and analyses performed, the table was set, the results of which are described below. Using the combined AHP and TOPSIS methods, the best available GTS-55 cast iron option was determined. The discrepancy in the results obtained with the actual conditions is somewhat justified due to data fluctuations related to the properties of the options.

1. Elkabir G, Rosen A (1981) Effect of microstructure on the fragmentation characteristics of malleable cast iron materials. Materials Science and Engineering 51(2): 265-269.
2. Ovchinnikov VI, Girenkov SG, Sharkov VA (1983) The influence of the structure and mechanical properties of malleable cast iron on its strength. Metal Science and Heat Treatment 25(2): 169-171.
3. Ponomarev AS, Sosenushkin EN, Klimov VN (2012) Effect of process features of pressure treatment on the microstructure and quality of parts of pipeline fittings from high strength cast iron. Metal Science and Heat Treatment 54: 22-27.
4. Li J, Liwei L (2015) An MCDM Model based on KL-AHP and TOPSIS and its application to weapon system evaluation. Atlantis Press 257-262.
5. Roy J, Majumder A, Saha SC (2014) Optimization of welding parameters of submerged arc welding using analytic hierarchy process (AHP) based on Taguchi technique. Journal of The Institution of Engineers (India): Series C 95: 159-168.
6. Chakladar ND, Chakraborty SA (2008) A combined TOPSIS-AHP-method-based approach for non-traditional machining processes selection. Proceedings of the Institution of Mechanical Engineers 222(12): 1613-1623.
7. Chen CT (2000) Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets and Systems 114(1): 1-9.
8. Khaira A, Dwivedi RK (2018) A state-of-the-art review of analytical hierarchy process. Materials Today 5(2): 4029-4035.
9. Prakash C, Barua MK (2015) Integration of AHP-TOPSIS method for prioritizing the solutions of reverse logistics adoption to overcome its barriers under fuzzy environment. Journal of Manufacturing Systems 37(3): 599-615.
10. Karahalios H (2017) The application of the AHP-TOPSIS for evaluating ballast water treatment systems by ship operators. Transportation Research Part D 52: 172-184.
11. Senthil S, Srirangacharyulu B, Ramesh A (2014) A robust hybrid multi-criteria decision-making methodology for contractor evaluation and selection in third-party reverse logistics. Expert Systems with Applications 41(1) 50-58.
12. Ishizaka A, Labib A (2011) Review of the main developments in the analytic hierarchy process. Expert Systems with Applications 38(11): 14336-14345.
13. Wang JJ, Yang DL (2007) Using a hybrid multi-criteria decision aid method for information systems outsourcing. Computers & Operations Research 34(12): 3691-3700.
14. Vaidya OS, Kumar S (2006) Analytic hierarchy process: An overview of applications. European Journal of Operational Research 169(1): 1-29.
15. Askeland RD, Haddleton F, Green P, Robertson H (1996) The science and engineering of materials. Springer, Germany.
16. Kou G, Ergu D, Peng Y, Shi Y (2013) Data Based for AHP/NHP. Quantitative Management. Springer, Germany.
17. Wang TS, Chang TH (2007) Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment. Expert Systems with Applications 33(4): 870-880.
18. Rayhanizadeh A, Towhidi N, Ebrahimnejad S, Shajari Y (2020) A fuzzy approach to selecting the electric arc furnace metallic charge materials. Engineering Research Express 2(2): 025009.
19. Ceotto D (2013) Thermal diffusivity, viscosity and prandtl number for molten iron and low carbon steel. High Temperature 51(1): 131-134.
20. Lomake EP, Malyi AF, Lukashchuk TI (1988) Effect of the thermal state of the mold on the properties of castings of cast iron pipeline fittings. Journal of Chemical and Petroleum Engineering 24: 94-95.