- Submissions

Full Text
Evolutions in Mechanical Engineering
Anisotropy Effects and Cosmymetry of Convective Flows for Nanofluids in Porous Medium
Abdelhafez MA*
Egypt
*Corresponding author: Abdelhafez MA, Sohag, Egypt
Submission: July 03, 2019;Published: September 24, 2019

ISSN 2640-9690 Volume3 Issue1
Abstract
The planar problem of convection in a porous rectangle saturated with a heat-conducting nanofluid is considered. Based on the Darcy-Boussinesq equations, taking into account the Soret effect and assuming the anisotropy of a fluid and a medium, an instability analysis of quiescent state is studied. The conditions under which the problem is being cosymmetric one are established and explicit formulas for the critical Rayleigh numbers are derived. The finite difference methods are developed with preservation of cosymmetry property.
Keywords: Convection; Nanofluid; Porous media; Anisotropy; Cosymmetry
Introduction
To simulate the motion of liquids and gases in porous media, the Darcy – Boussinesq model is usually used, on the basis of which important results were obtained on the instability of mechanical equilibrium and the formation of convective modes [1]. In [2] for the problem of heating a layer of a porous medium saturated with a heat-conducting fluid, a nontrivial effect of a branch of a family of stationary convective regimes from a state of rest was discovered. This phenomenon has been explained in [3] based on the theory of cosymmetric dynamical systems for which the occurrence of continuous families of stationary states with a variable stability spectrum along the family is possible. The goal of this work is the development of methods for modeling the convection of nanofluids, taking into accounts the anisotropy of the properties of the problem, as well as the use of cosymmetry of the corresponding system of equations for obtaining analytical results and developing computational schemes.
Equations of Convection of Nanofluid in a Porous Medium
The problem of the emergence of gravitational convection of a heat-conducting fluid with nanoparticles in a rectangular region is considered D=[0,a]×[0,b], filled with a porous medium and heated from the bottom. At the boundary, no-flow conditions and a linear height distribution of temperature and concentration of nanoparticles are specified. For stream function ψ(x,y,t), temperature deviations θ(x,y,t) and concentration c(x,y,t)). From the given linear profiles, a system of three equations is written in dimensionless variables:

Here, the dot denotes time differentiation t, Δ = ∂x2 + ∂y2 --- laplacian, μij--- reverse permeability coefficients, λT --- Rayleigh temperature number and λC --- Rayleigh concentration number. Thermal conductivity operator LT in the case of anisotropy, it is given by a formula with coefficients dijCT;
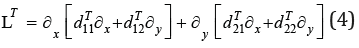
Operators and are obtained from (4) replacing dijT to dijC and dijCT respectively. The boundary conditions can be written as,
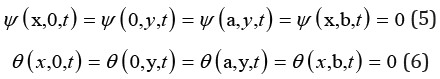
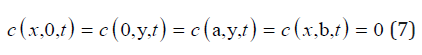
Cosymmetry
In [4] it is shown that the problem of convection of a heatconducting fluid in a porous medium, taking into account the anisotropy of the properties of the medium, is cosymmetric. For the system (1)-(7) the conditions for the existence of a linear in variables cosymmetry problem are established.
Lemma. Vector function
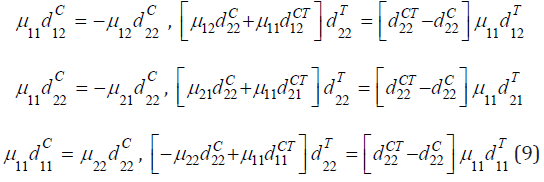
will be the cosymmetry of the system (1)-(7) under the following conditions for the task parameters
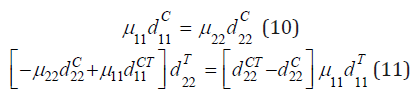
The proof consists in directly verifying the orthogonality of the cosymmetry and the vector field of the problem (1)-(3). Next, we consider the case of orthotropic nanofluids and media, i.e. μij = dijT = dijC = dijCT = , i ≠ j , i, j = 1, 2 . Then from (9) the following two conditions remain
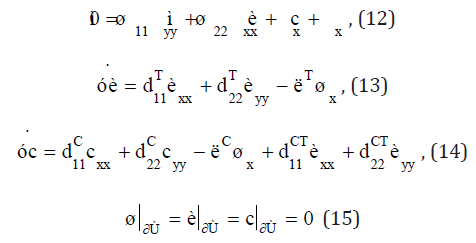
The spectral problem of the stability of mechanical equilibrium is σ (-- decrement)
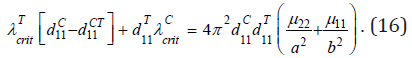
Under the conditions of cosymmetry and for the case of monotonic instability σ = 0 from (12)-(15) derives a relation relating the critical Rayleigh numbers λT and λC:
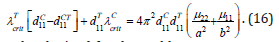
This formula, obtained for the problem parameters satisfying the conditions of cosymmetry, allows one to determine the subregions of parameters for which the critical values of the temperature and concentration Rayleigh numbers are explicitly.
Numerical Results
In the general case of the anisotropic properties of nanofluid and porous media, the analysis of the instability of mechanical equilibrium usually requires a computational experiment. Similarly [4] a numerical scheme of the finite-difference method is constructed, preserving the cosymmetry of the problem. The coordinates x and y are introduced into the grid. Xi = ih , i = 0,1, ..., n + 1, h = a / (n + 1) , yj = jg , j = 0,1, ...., m + 1 , g = b / (m + 1) . The unknowns are the values of the current function, temperature, and the concentration of nanoparticles in the internal nodes. Due to boundary conditions ψij = θij = cij = for i = 0, n + 1 or j = 0, m + 1. The following vectors are introduced ( ψ11, ψ12, ...,ψmn ), È = ( θ11, θ12, ...,θmn ), C = ( c11, c12, ...,cmn ). System (12)-(14) matches the grid problem
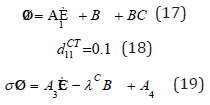
where the matrix A1 meets the discrete version of the operator M0 , matrices A2, A3 and A4 are approximations of operators , LT LC and LCT respectively, the matrix gives a difference analogue of the derivative with respect to x. For the case of monotone instability, confirmatory calculations were performed, which determined the grid parameters to ensure sufficient accuracy in calculating the loss of stability of mechanical equilibrium. On the plane of the temperature and concentration Rayleigh numbers, neutral curves were constructed for various combinations of control parameters and the areas of monotonic and oscillatory instability were calculated. The dependence on the thermal diffusion parameters of the concentration Rayleigh number is established, at which the vibrational instability precedes the monotonic one. The derived conditions on the parameters that ensure the cosymmetry of the problem, and explicit formulas for the critical Rayleigh numbers can be used to estimate the occurrence of convection of a nanofluid saturating the anisotropic porous medium in a general situation. In Table 1 Presents the results of calculating the critical numbers in case of violation of the conditions of cosymmetry and their comparison with the values of the parameters that satisfy the conditions (11).
Table 1:The critical values of the temperature Rayleigh number at various λC and dCT22
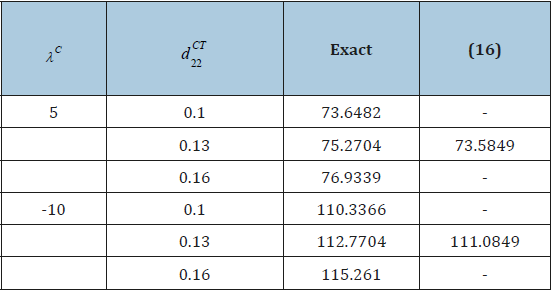
The calculations were carried out at fixed values of the parameters: μ11 = 1.3 , μ22 = 1, d11T =1 , d22T= 1.3, d11C=0.5, d22C = 0.65 dCT11 = 0.1 and for the grid 24 ×12 . For λC =5 mechanical equilibrium loses stability as a result of monotonic instability, and for λC = −10 SS-- due to oscillatory instability. The obtained values are quite close to the calculations by the formula (16), evaluating the critical number in the case of monotone instability [5].
References
- Nield DA, Bejan A (2013) Convection in Porous Media. (4th edn), Springer, New York, USA.
- Lyubimov DV (1975) Convective motions in a porous medium heated from below. Journal of Applied Mechanics and Technical Physics 16(2): 131-137.
- Yudovich VI (1991) Cosymmetry, degeneration of solutions of operator equations, and onset of a filtration convection. Mathematical Notes of the Academy of Sciences of the USSR 49(5): 540-545.
- Abdelhafez MA, Tsybulin VG (2017) Anisotropy effect on the convection of a heat-conducting fluid in a porous medium and cosymmetry of the darcy problem. Fluid Dynamics 52(1): 49-57.
- Abdelhafez MA, Tsybulin VG (2017) Numerical simulation of convective motion in an anisotropic porous medium and cosymmetry conservation. Computational Mathematics and Mathematical Physics 57(10): 1706-1719.
© 2019 Abdelhafez MA. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






