Control of a SCARA Robot Using Feedback Linearization and Kalman Filter Observer

The importance of using robot in daily life is shown, when human life is at risk. For instance, in high-risk industrial places such as working alongside the melting furnaces or neutralize mines on the battlefield and such high-risk areas. In additional, human accuracy is reduced when doing repetitive work. Mentioned reasons, the use of robots has become prevalent in many diverse industries and locations [1-8]. SCARA robot is a kind of usual robots which is used for welding, painting, assembly and material handling [9]. This robot consists of three degree of freedom. Economic justification for the cost of installing a robot must be considered some important things. The robot control system must have some necessities like short time of cycling, continuous and accurately tracking. To achieve the short time cycling; the robot needs to have enough fast response, to get to high tracking accuracy, the tracking error should be very low [10]. The importance problem in using of the robot is accurate control method to guiding the end effector to the desired position quickly.

There are various applicable controller methods that can be divided in to different branches such as model-base or none modelbase [11-21]; (Figure 1 & 2), adaptive [22-28], and intelligence [29- 36] methods. Tuning the parameters of a controller method which contains a high number of tunable parameters, is very crucial and can be very cumbersome. To accomplish this process, one way which is very common, is employing an efficient optimization method [37-95]. By determining a proper cost function, the optimization algorithm can tune the controller parameters optimally. It worth nothing that, selecting a power full optimization method is very vital and must be done regarding the number of tunable parameters and the complexity of the ultimate cost function. Recently, some novel and effective population optimization algorithms have been presented that can be used for this goal.

The aim of this paper is to introduce an applicable and effective controller for controlling a SCARA robot in present of disturbance. To do so, feedback linearization (FL) method which is a nonlinear and effective controller is selected. Sensitivity to noise is a disadvantage of FL. To overcome this problem using a kalman filter to estimate the state variables is suggested.

This paper complained of several sections. Section 2 described problems, parameter and explained the assumptions. In section 3 is reported the dynamic modeling direct kinematic of SCARA robot. 4th section depicted the controller. Stochastic feedback linearization LQG with Kalman filter is used to control the SCARA manipulator robot. This controller can estimate parameter and identified original signal in comparison of disturbance signals. In section 5 demonstrated the results simulation by Figure 1 and curves. Figure 1 of tracking is pictured in this section also, which validated the successful performance of controller. Finally, in ending section explained the conclusions of paper.

In this paper the SCARA robot with 3 degree of freedom is controlled. This robot is RRP type and is assumed all of arms is rigid body. The friction in each joint is negligible. The original mass moment of inertia is in Z-direction. There is no mass moment of inertia in other plane. The final joint has a force in Z-direction which is shown in Figure 1. G1 and G2 are manipulator center of mass.

In this section the dynamic equation of SCARA robot is obtained. For this purpose, the Euler-Lagrangian method is used to derive dynamic equations. So, the kinematic and potential energy of the system must be computed to use in Lagrangian equation. The kinematic and potential energy of the system is obtained as [16]:

Where x_ci and y_ci are the center of mass position of i_th manipulator, m₁,m₂ and m₃ are mass of manipulators, I_c1 and I_c2are the moment of inertia around center of mass manipulator 1 and 2 respectively and i è is the angel of the th i manipulator which is shown in Figure 2, g is the gravity acceleration and z is the height of center of mass manipulator 3. x_ci and y_ci are [16]:

So, the velocity of each manipulator is

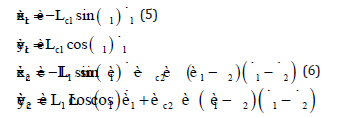
Where L_ci and L_ci are the distance between center of mass i_th manipulator and i_th joint.

So, the Lagrangian of the system is obtained as [4,11,34]:

L = K −U

Where L is the Lagrangian function. By using the Euler-Lagrange formulation the dynamic equation of the system is obtained as below:

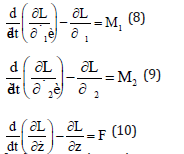
In these equations q is states of the system and defined as:

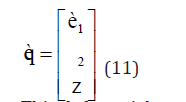
This deferential equation can be expressed in matrix form as:

Where the matrices M, C, and G are represented the 3×3 inertia matrix, 3×1 Centripetal-Coriolis

Matrix terms, and 3×1gravity matrix, respectively and T are 3×1 matrix which is defined as below:

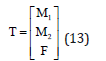
In state space the state is defined as below:

In this section the stochastic LQE feedback linearization controller with Kalman filter, is designed. Feedback linearization: In feedback linearization method by equaling the nonlinear system in to a stable linear system, the control law can be derived as nonlinear system as below [1,16,26]. The stable linear system has been considered as below:

Where matrix A and B be are defied as:

Where E is the vector of state variable of the linear system and V is system input vector. The nonlinear system can be obtained also as:

Where X is the state variable of the nonlinear system, F and G are derived from equations 14 to 16.

With considering E as error we have:

So, the controller law for nonlinear system derived as:

LQE controller

In control theory, the Linear-Quadratic-Estimator (LQE) control problem is one of the most fundamental optimal control problems [20]. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs. Moreover, the solution is unique and constitutes a linear dynamic feedback control law that is easily computed and implemented (Figure 3). Finally, the LQE controller is also fundamental to the optimal control of perturbed non-linear systems.

The linear system is considered as below:

In this problem C is 6x6 identity matrix.

Where the vector E is state variable, the vector V is control input, the vector Y is measurement output and the vector n are additive white Gaussian system noise and w is additive white Gaussian measurement noise. The LQE controller is specified by the following equations:

Where the matrix K is Kalman gain which is obtained from Kalman filter equation.

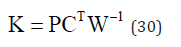
Where

Where in the above differential equations W the covariance of w and N is the covariance of n.

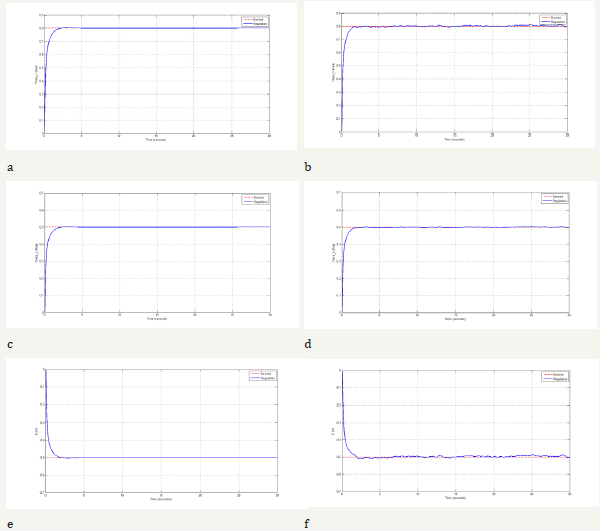
To regulate the angle system by controller 1, 2 θ θ and z are main parameters which are considered. The simulation results are Investigation in two Conditions, one with present disturbance and the other without consider disturbance. Also, the Measured and Estimated states are illustrated in Figure 4a-4f for regulation and in Figure 5a-5f for tracking purpose.

In this investigation, the SCARA robot control is presented. SCARA robot is controlled by a stochastic feedback linearization LQE with Kalman filter. This controller can control the robot successfully and identified original signals in presence of the disturbance’s signals. In feedback linearization method by equaling the nonlinear system in to a stable linear system, the control law can be derived as nonlinear system. LQE controller concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs. This combination of useful control methods is already set to lead the system to the desired position in presence of disturbance as is evidenced in the simulation results and Figure 1-5.

Figure 1:Schematic of front view of SCARA robot [16].

Figure 2:Schematic of left view of SCARA robot [16].

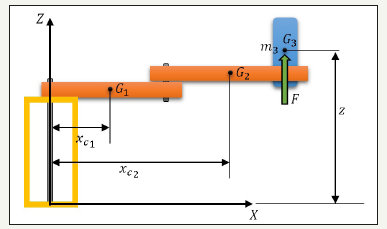
Figure 3:Schematic Stochastic controller.

Figure 4:Estimation of the state variables, a) θ1without noise, b) θ1with noise, c) θ2 without noise, d) θ2 with noise, e) z without noise, f) z with noise.

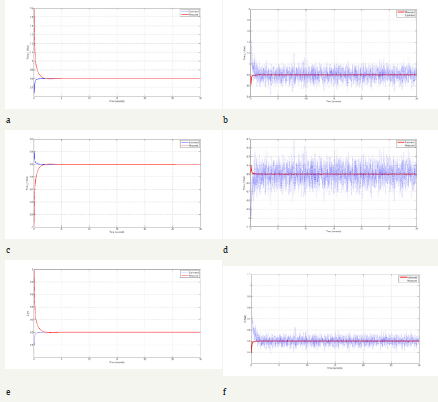
Figure 5:Regulation for variable state, a) θ1 without noise, b) θ1 with noise, c) θ2 without noise ,d) θ2 with noise, e) z without noise ,f) z with noise.

1. Zakeri E, Farahat S, Moezi SA, Zare A (2016) Robust sliding mode control of a mini unmanned underwater vehicle equipped with a new arrangement of water jet propulsions: Simulation and experimental study. Applied Ocean Research 59: 521-542.
2. Eliot E, Deepak B, Parhi DR (2012) Design & kinematic analysis of an articulated robotic manipulator. IJMIE 3(1): 105-108.
3. Parhi DR, Singh MK (2009) Navigational strategies of mobile robots: A review. International Journal of Automation and Control 3(2-3): 114- 134.
4. Moezi SA, Rafeeyan M, Zakeri E, Zare A (2016) Simulation and experimental control of a 3-RPR parallel robot using optimal fuzzy controller and fast on/off solenoid valves based on the PWM wave. ISA Transactions 61: 265-286.
5. Deepak B, Parhi D (2012) PSO based path planner of an autonomous mobile robot. Open Computer Science 2(2): 152-168.
6. Zakeri E, Farahat S, Moezi SA, Zare A (2016) Path planning for unmanned underwater vehicle in 3d space with obstacles using spline-imperialist competitive algorithm and optimal interval type-2 fuzzy logic controller. Latin American Journal of Solids and Structures 13(6): 1054-1085.
7. Parhi DR (2005) Navigation of mobile robots using a fuzzy logic controller. Journal of Intelligent &Robotic Systems 42(3): 253-273.
8. Zakeri E, Bazargan LY, Eghtesad M (2012) Simultaneous control of GMAW process and SCARA robot in tracking a circular path via a cascade approach. Trends in Applied Sciences Research 7(10): 845-858.
9. Luh JY (1983) An anatomy of industrial robots and their controls. IEEE Transaction On Automatics Control 28(2): 133-153.
10. Wang SP, Kuo CY (1988) Nonlinear robust robot control in cartesian coordinate. American Control Conference, USA.
11. Moezi SA, Rafeeyan M, Ebrahimi S (2015) Sliding mode control of 3-RPR parallel robot on the optimal path using cuckoo optimization algorithm. Modares Mechanical Engineering 15(2): 147-158.
12. Parhi DR, Singh MK (2008) Intelligent fuzzy interface technique for the control of an autonomous mobile robot. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 222(11): 2281-2292.
13. Mohanty PK, Parhi DR (2014) Navigation of autonomous mobile robot using adaptive neuro-fuzzy controller. In Intelligent Computing, Networking, and Informatics pp. 521-530.
14. Zakeri E, Moezi SA, Eghtesad M (2017) Tracking control of ball on sphere system using tuned fuzzy sliding mode controller based on artificial bee colony algorithm. International Journal of Fuzzy Systems 20(1): 1-4.
15. Patle BK, Parhi DR, Jagadeesh A, Kashyap SK (2016) Probabilistic fuzzy controller based robotics path decision theory. World Journal of Engineering 13(2): 181-192.
16. Zakeri E, Moezi SA, Bazargan-Lari Y, Zare A, Eghtesad M (2016) Robot manipulation by a new hybrid feedback linearization adaptive neuro- fuzzy control method. In: 24th Annual International Conference on Mechanical Engineering, pp. 26-28.
17. Zare M, Zakeri E, Sadeghi J, Farahat S (2016) Tracking control of an unmanned aerial vehicle using cascade configuration of fuzzy logic controllers in presence of windflaw. International Journal of Advanced and Applied Sciences 3(8): 43-51.
18. Chouhan AS, Parhi DR, Chhotray A (2018) Control and balancing of twowheeled mobile robots using sugeno fuzzy logic in the domain of AI techniques. International Journal of Scientific & Engineering Research 9(4): 111-121.
19. Mohanty PK, Parhi DR (2014) A new intelligent motion planning for mobile robot navigation using multiple adaptive neuro-fuzzy inference system. Applied Mathematics & Information Sciences 8(5): 2527-2535.
20. Zakeri E, Moezi SA, Zare M, Rad MP (2014) Control of puma-560 robot using feedback linearization control method and kalman filter estimator for regulation and tracking purpose. J Math Comput Sci 11(4): 264-276.
21. Bazargan-Lari Y, Zakeri E, Ghahramani AR, Bazargan-Lari K, Moezi SA (2012) Disturbance rejection control of 3-D overhead gantry crane system for regulation purpose. In: National Conference on Mechanical Engineering, pp. 22-23.
22. Kundu S, Parhi DR (2016) Navigation of underwater robot based on dynamically adaptive harmony search algorithm. Memetic Computing 8(2): 125-146.
23. Moezi SA, Zakeri E, Bazargan LY, Tavallaein M (2014) Control of a ball on sphere system with adaptive neural network method for regulation purpose. Journal of Applied Sciences 14(17): 1984-1989.
24. Zakeri E, Moezi SA, Bazargan-Lari Y (2013) Control of a ball on sphere system with adaptive feedback linearization method for regulation purpose. Majlesi Journal of Mechatronic Engineering 2(3): 23-27.
25. Parhi DR, Mohanty PK (2016) IWO-based adaptive neuro-fuzzy controller for mobile robot navigation in cluttered environments. The International Journal of Advanced Manufacturing Technology 83(9-12): 1607- 1625.
26. Zakeri E, Ghahramani A, Moezi SA, Bazargan-Lari Y (2012) Adaptive feedback linearization control of a ball on sphere system. In: International conference on mechanical engineering and advanced technology.
27. Sahu S, Kumar PB, Parhi DR (2017) Design and development of 3-stage determination of damage location using Mamdani-adaptive genetic-Sugeno model. Journal of Theoretical and Applied Mechanics 55(4): 1325- 1339.
28. Kumar PB, Sahu C, Parhi DR (2018) A hybridized regression-adaptive ant colony optimization approach for navigation of humanoids in a cluttered environment. Applied Soft Computing 68: 565-585.
29. Abdalla TY, Abed AA, Ahmed AA (2017) Mobile robot navigation using PSO-optimized fuzzy artificial potential field with fuzzy control. Journal of Intelligent & Fuzzy Systems 32(6): 3893-3908.
30. Kumar A, Kumar PB, Parhi DR (2018) Intelligent navigation of humanoids in cluttered environments using regression analysis and genetic algorithm. Arabian Journal for Science and Engineering 43(12): 1-24.
31. Moezi SA, Zakeri E, Bazargan-Lari Y, Khalghollah M (2014) Fuzzy logic control of a ball on sphere system. Advances in Fuzzy Systems 2014: 17.
32. Zare M, Sadeghi J, Farahat S, Zakeri E (2014) Regulating and helix path tracking for unmanned aerial vehicle (UAV) using fuzzy logic controllers. Journal of mathematics and computer science 13(1): 71-89.
33. Mahapatra S, Jha AK, Patle BK, Parhi DR (2012) Fuzzy logic control of a WMR. In Computing, Communication and Applications (ICCCA).
34. Zakeri E, Farahat S (2015) Safe path planning and control of an Unmanned Underwater Vehicle (UUV) using particle swarm optimization and fuzzy logic control method. Modares Mechanical Engineering 14(14): 199-210.
35. Bazargan-Lari Y, Eghtesad M, Ghahramani A, Zakeri E, Lari KB (2012) A neural network control for 3-D overhead gantry crane system with uncertain load disturbance. In: Proceedings of the 20th Annual International Conference on Mechanical Engineering.
36. Zakeri E, Farahat S, Moezi SA, Zare M (2016) Optimal robust control of an unmanned underwater vehicle independent of hydrodynamic forces using firefly optimization algorithm. In: 24th Annual International Conference on Mechanical Engineering-ISME.
37. Deepak BBVL, Parhi DR, Kundu S (2012) Innate immune based path planner of an autonomous mobile robot. Procedia Engineering 38: 2663-2671.
38. Mohanty PK, Pandey KK, Parhi DR (2014) MANFIS approach for path planning and obstacle avoidance for mobile robot navigation. In ICT and Critical Infrastructure: Proceedings of the 48th Annual Convention of Computer Society of India I: 361-370.
39. Jena SP, Parhi DR, Mishra D (2015) Response of cracked cantilever beam subjected to traversing mass. American Society of Mechanical Engineers.
40. de Oliveira VYM, de Oliveira R, Affonso C (2018) A novel cuckoo search approach enhanced with genetic replacement of abandoned nests applied to optimal allocation of DG units. IET Generation, Transmission & Distribution 12(13): 3353-3362.
41. Dao TP, Huang SC, Thang PT (2017) Hybrid Taguchi-cuckoo search algorithm for optimization of a compliant focus positioning platform. Applied Soft Computing 57: 526-538.
42. Yang B, Wang Z, Yang Y, Kang Y, Li X (2017) Optimum fixture locating layout for sheet metal part by integrating kriging with cuckoo search algorithm. The International Journal of Advanced Manufacturing Technology 91(1-4): 327-340.
43. Kumar PB, Parhi DR (2017) Vibrational characterization of a human femur bone and its significance in the designing of artificial implants. World Journal of Engineering 14(3): 222-226.
44. Mohanty JR, Parhi DR, Ray PK, Verma BB (2009) Prediction of residual fatigue life under interspersed mixed‐mode (I and II) overloads by Artificial Neural Network. Fatigue & Fracture of Engineering Materials & Structures 32(12): 1020-1031.
45. Parhi DR (2018) Advancement in navigational path planning of robots using various artificial and computing techniques. Int Rob Auto J 4(2): 133-136.
46. Jena SP, Parhi DR (2016) Response of damaged structure to high speed mass. Procedia Engineering 144: 1435-1442.
47. Mohanty PK, Kumar S, Parhi DR (2015) A new ecologically inspired algorithm for mobile robot navigation. In Proceedings of the 3rd International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA) pp. 755-762.
48. Parhi DR, Behera AK, Sahoo PK (1997) Dynamic response of beams with a moving mass. Journal-Aeronautical Society of India 49: 69-75.
49. Balasubramanian KR, Sivapirakasam SP, Anand R (2014) Dynamic deflection of a cantilever beam carrying moving mass. In Applied Mechanics and Materials 592: 1040-1044.
50. Parhi DR, Das HC (2008) Smart crack detection of a beam using fuzzy logic controller. Int J Comput Intell: Theory Pract 3(1): 9-21.
51. Parhi DR (2000) Navigation of multiple mobile robots in an unknown environment Doctoral dissertation, University of Wales, Cardiff, UK.
52. Wei W, Song H, Li W, Shen P, Vasilakos A (2017) Gradient-driven parking navigation using a continuous information potential field based on wireless sensor network. Information Sciences 408: 100-114.
53. Moezi SA, Zakeri E, Bazargan-Lari Y, Zare A, Eghtesad M (2016) On the application of genetic and cuckoo optimization algorithms to a 2&3-dimensional connecting rod. IJSTM 39: 39-49.
54. Ma F, Chen YW (2018) Probabilistic assessment of vessel collision risk: An evidential reasoning and artificial potential field-based method. In Multi-Criteria Decision Making in Maritime Studies and Logistics pp. 123-149.
55. Pandey KK, Pandey A, Chhotray A, Parhi DR (2016) Navigation of mobile robot using type-2FLC. Proceedings of the International Conference on Signal, Networks, Computing, and Systems, pp. 137-145.
56. Pandey A, Parhi DR (2017) Optimum path planning of mobile robot in unknown static and dynamic environments using Fuzzy-Wind Driven Optimization algorithm. Defence Technology 13(1): 47-58.
57. Mohanty PK, Parhi DR (2015) A new hybrid optimization algorithm for multiple mobile robots navigation based on the CS-ANFIS approach. Memetic Computing 7(4): 255-273.
58. Moezi SA, Ghahramani A, Zakeri E, Bazargan-Lari Y, Assadsangabi B (2012) Shape optimization of BELTs via genetic algorithm. In: International conference on mechanical engineering and advanced technology.
59. Singh MK, Parhi DR (2011) Path optimisation of a mobile robot using an artificial neural network controller. International Journal of Systems Science 42(1): 107-120.
60. Ranjan KB, Sahu S, Parhi Dayal R (2014) A new reactive hybrid membership function in fuzzy approach for identification of inclined edge crack in cantilever beam using vibration signatures. Applied Mechanics and Materials 592: 1996-2000.
61. Moezi SA, Zakeri E, Zare A (2018) Structural single and multiple crack detection in cantilever beams using a hybrid Cuckoo-Nelder-Mead optimization method. Mechanical Systems and Signal Processing 99: 805- 831.
62. Moezi SA, Zakeri E, Zare A (2018) A generally modified cuckoo optimization algorithm for crack detection in cantilever euler-bernoulli beams. Precision Engineering 52: 227-241.
63. Yadao AR, Parhi DR (2016) The influence of crack in cantilever rotor system with viscous medium. International Journal of Dynamics and Control 4(4): 363-375.
64. Biswas P, Navaneethkrishnan B, Anand G, Omkar SN (2018) System identification of a small scaled helicopter using simulated annealing algorithm. Indian Control Conference (ICC) 2018: 335-339.
65. Palacios JA, Olvera D, Urbikain G, Elías Zúñiga A, Martínez RO, et al. (2018) Combination of simulated annealing and pseudo spectral methods for the optimum removal rate in turning operations of nickel-based alloys. Advances in Engineering Software 115: 391-397.
66. Zeng R, Wang Y (2018) A chaotic simulated annealing and particle swarm improved artificial immune algorithm for flexible job shop scheduling problem. EURASIP Journal on Wireless Communications and Networking 2018(1): 101.
67. Moezi SA, Zakeri E, Bazargan LY, Zare A, Branch S (2009) 2D Shape optimization via genetic algorithm. J Math Comput Sci 11: 209-217.
68. Das HC, Parhi DR (2009) Application of neural network for fault diagnosis of cracked cantilever beam. In Nature & Biologically Inspired Computing.
69. Parhi DR, Das HC (2008) Structural damage detection by fuzzy-gaussian technique. International Journal of Mathematics and Mechanics 4: 39- 59.
70. Parhi DR, Pothal JK (2011) Intelligent navigation of multiple mobile robots using an ant colony optimization technique in a highly cluttered environment. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 225(1): 225-232
71. Parhi DR, Agarwalla DK, (2012) Diagnosis of damaged al cantilever beam subjected to free vibration by numerical and experimental method. IJAICR 4(2): 71-77.
72. Moezi SA, Zakeri E, Zare A, Nedaei M (2015) On the application of modified cuckoo optimization algorithm to the crack detection problem of cantilever Euler-Bernoulli beam. Computers & Structures 157: 42-50.
73. Kundu S, Mishra M, Parhi DR (2014) Autonomous navigation of underwater mobile robot based on harmony search optimization. In: Power Electronics, Drives and Energy Systems (PEDES).
74. Zakeri E, Moezi SA, Bazargan LY, Zare A (2017) Multi-tracker optimization algorithm: a general algorithm for solving engineering optimization problems. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering 41(4): 315-341.
75. Jena PC, Parhi DR, Pohit G (2014) Theoretical, numerical (FEM) and experimental analysis of composite cracked beams of different boundary conditions using vibration mode shape curvatures. International Journal of Engineering and technology 6: 509-518.
76. Xu QL, Cai MM, Zhao LH (2017) The robot path planning based on ant colony and particle swarm fusion algorithm. Chinese Automation Congress (CAC) 2017: 411-415.
77. Elmi A, Topaloglu S (2017) Cyclic job shop robotic cell scheduling problem: Ant colony optimization. Computers & Industrial Engineering 111: 417-432.
78. Liu J, Yang J, Liu H, Tian X, Gao M (2017) An improved ant colony algorithm for robot path planning. Soft Computing 21(19): 5829-5839.
79. Sahu S, Kumar PB, Parhi DR (2017) Intelligent hybrid fuzzy logic system for damage detection of beam-like structural elements. Journal of Theoretical and Applied Mechanics 55(2): 509-521.
80. Agarwalla DK, Parhi DR (2013) Effect of crack on modal parameters of a cantilever beam subjected to vibration. Procedia Engineering 51: 665- 669.
81. Moezi SA, Zakeri E, Bazargan LY, Zare A (2015) 2&3-dimensional optimization of connecting rod with genetic and modified cuckoo optimization algorithms. Iranian Journal of Science and Technology 39(1): 39.
82. Parhi DR, Deepak BB, Nayak D, Amrit A (2012) Forward and inverse kinematic models for an articulated robotic manipulator. International Journal of Artificial Intelligence and Computational Research 4(2): 103- 109.
83. Deepak B, Parhi DR (2011) Kinematic analysis of wheeled mobile robot. Automation &Systems Engineering 5(2): 96-111.
84. Behera RK, Parhi DR (2007) Vibration analysis of a beam carrying a moving mass. ICSV14, Cairns, Australia.
85. Das SS, Parhi DR, Mohanty S (2018) Insight of a six layered neural network along with other AI techniques for path planning strategy of a robot. Emerging Trends in Engineering, Science and Manufacturing (ETESM-2018), IGIT Sarang, India.
86. Dash AK, Parhi DR (2011) Development of an inverse methodology for crack diagnosis using AI technique. International Journal of Computational Materials Science and Surface Engineering 4(2): 143-167.
87. Kumar PB, Pandey KK, Sahu C, Chhotray A, Parhi DR (2017) A hybridized RAAPSO approach for humanoid navigation. Engineering (NUiCONE), IEEE.
88. Brahmbhatt N, Patel M, Deb D (2017) Micro-controller driven wind turbine blade cleaning peripheries. Advances in Computing, Communications and Informatics (ICACCI), IEEE.
89. Xiong H, Diao X (2017) Cable tension control of cable-driven parallel manipulators with position-controlling actuators. In: Robotics and Biomimetics (ROBIO), 2017 IEEE International Conference, pp. 31763-1768.
90. Abdolshah S, Zanotto D, Rosati G, Agrawal SK (2017) Optimizing stiffness and dexterity of planar adaptive cable-driven parallel robots. Journal of Mechanisms and Robotics 9(3): 031004.
91. Khan IA, Yadao A, Parhi DR, Ghazaly NM, El Sharkawy M, et al. (2014) Fault diagnosis of cracked cantilever composite beam by vibration measurement and RBFNN. Journal of Mechanical Design 1(1): 1-4.
92. Panigrahi I, Parhi DR (2009) Dynamic analysis of Cantilever beam with transverse crack. 14th National Conference on Machines and Mechanisms, India.
93. Das HC, Parhi DR (2009) Detection of the crack in cantilever structures using fuzzy Gaussian inference technique. AIAA J 47(1): 105-115.
94. Parhi DR, Dash AK, Das HC (2011) Formulation of a genetic algorithm- based methodology for multiple crack detection in a beam structure. Australian Journal of Structural Engineering 12(2): 127-139.
95. Mohanty PK, Parhi DR (2013) Controlling the motion of an autonomous mobile robot using various techniques: A review. Journal of Advance Mechanical Engineering 1(1): 24-39.