- Submissions

Full Text
Evolutions in Mechanical Engineering
Research Progress on Mechanical Properties Of 3D Braided Composites
Zhonggui Li1,2, Zhangxin Guo1,2,3*, Junjie Cui1,4, Ming Zhu1,3, Qi HE1,3, Yongcun Li1,4 and Yunbo Luan1,3
1Institute of Applied Mechanics, China
2State Key Laboratory for Strength and Vibration of Mechanical Structures, China
3Shanxi Key Laboratory of Material Strength & Structural Impact, China
4National Demonstration Center for Experimental Mechanics Education, China
*Corresponding author:Zhangxin Guo, Institute of Applied Mechanics, College of Mechanical and Vehicle Engineering, China
Submission: December 4, 2018;Published: December 13, 2018

ISSN 2640-9690 Volume2 Issue2
Abstract
Due to high specific strength, specific stiffness and flexibility in their design, braid composites have been widely used in various engineering structures. In the practical engineering application, braid composites are in a multidirectional stress state in most cases, in which the material failure mechanism is very complex. Moreover, the performance degradation of stiffness and strength is more complex. The microstructure of 3D braided composites is extremely complicated and shows intensive inhomogeneity and anisotropy, which results in considerable difficulties in the researches of macro-meso-mechanical properties and damage mechanics. This review summarized different research methods such as prediction of strength, lowvelocity impact and fatigue failure.
Keywords: Braid composites; Stress state; Failure mechanism; Tensile load; Low-velocity impact
Introduction
3D braided composite material takes integral braided preformed parts as reinforcement material without suture and mechanical processing. Meanwhile, it has good comprehensive performance indicators, such as high specific strength, high specific stiffness, especially in integrity, delamination resistance, resistance to impact and designability etc. Therefore, it has been widely used in the fields of aerospace, military industry, ships, sports goods, transportation and construction [1]. With the application of 3D braided composites more and more widely, many models have been developed to analyze their mechanical properties. These analyses are challenging due to the complexity of the architecture. The study of mechanical properties of 3D braided composites has important guiding significance for its structural design and application. This paper mainly introduces the work in recent years and the author’s research results from several aspects.
Prediction of Strength
The strength criterion as the basis of material failure in mechanical analysis and numerical simulation is an important part of the research on the strength properties of materials, and the strength characteristic is a main component of the mechanical properties. No strength criterion has been established specifically for 3D braided composite materials. Hence, strength criterion of existing unidirectional composites is adopted by the failure criterion of fiber bundle damage, including two types: one is the strength criterion for distinguishing failure modes, such as Hashin criterion [2], Puck criterion [3], Chang-Chang criterion [4]; the other is the multi-term criterion which does not distinguish the failure modes, such as Tsai-Wu criterion [5], Hoffman criterion [6], Tsai-Hill criterion [7]. Moreover, Hashin criterion and Tsai-Wu criterion are the most widely used in the damage analysis of 3D braided composites.
Sun et al. [8] developed a fiber-inclination mode (Figure 1) Based upon the Tsai-Wu criterion, they explored the effect of braid angle of 3D braided composites on tensile modulus and strength. The maximum strain failure criterion is used to obtain tensile curve of 3D braided composites [9]. Then, the uniaxial tensile strength was predicted and well verified by experiments. Lu et al. [10] presented an empirical failure criterion of strength, which based on existing strength theory of composite materials, to predict strength of 3D braided composites. Zeng et al. [11,12] developed a new type of finite element method (FEM) to obtain the local stress and strength. However, the numerical model was simplified to the unit cell which didn’t reflect the microscopic structure. Karkkainen [13-15] did some researches on strength analysis of textile composites. Song et al. [16,17] developed an arc-length method to measured inelastic properties of the matrix (the insitu properties) of 2D triaxial braided carbon fiber composites (2DTBC). Dong et al.
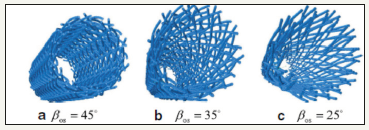
[18,19] simulated micro-stress combing the method of Asymptotic Expansion Homogenization (AEH) with finite-element model which introducing face cell and body cell. They found small braiding angle have better strength. Zhang et al. [20] analyzed Hashin and Tsai- Wu failure criterions as the result of identify damage initiation of the braiding yarns, respectively. They found Tsai-Wu failure criterions were better. The strength characterizations of the 3D braided composites using the representative unit cell (RUC) were reported in many references [21-23]. Xiao et al. [24] prosed an approximate method that the periodic meso structure in RUC in textile composites is approximated by sub-cells and each sub-cell is represented by a laminate with plies representing fiber tows and matrix to investigate the stress–strain. Lei et al. [25,26] presented representative volume cell (RVC) with interface zones and the periodic boundary conditions to analyze the tensile properties. Large amount of references on the strength characterizations of the 3D braided composite using RVC are reported. However, most of them were rectangular, which was not suitable for the cylindrical shaft. Hao et al. [27] built up the geometry models of cylindrical RVCs for 3D four directional cylindrical braided composite (Figure 2) with different braiding angles and fiber volume contents to research strength characterizations.
Figure 1:The fiber-inclination mode.
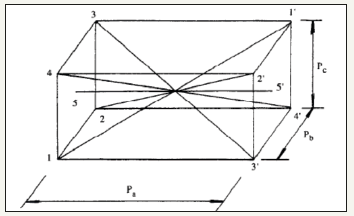
Figure 2:The 3D four directional cylindrical braided composite shafts.
Low Velocity
The dynamic mechanical behavior of composite materials is considered one of the most important properties by structural engineers. For instance, plastic behavior and damage under lowvelocity impact can possibly ensue during production, maintenance, repair, or the lifetime of structural composite components. A number of factors which can seriously damage composites include tool drop, flying debris, foreign object damage, etc. However, damage from low velocity impact is not visible to the naked eye but may affect the material’s residual mechanical properties. Compared with laminated composites, there is no delamination for three-dimensional (3D) braided composites under ballistic impact. Additionally, with the3D braiding technique, complex near-netshape preform, and composite structures can be manufactured. These features lead to the application of complex shaped braided composite structures in impact protection areas, such as debris impact protection of supersonic aircraft and spaceship. Heimbs et al. [28] developed the meso and macro-scale to study elastic energy stored during impact. Elias et al. [29] presented the ODM-PMC model to investigate damage mechanisms of 3D woven composites and estimated the residual properties of the material. Both a Macrohomogeneous model and a Meso-heterogeneous model were adopted in [30]. In the work of Rao et al. [31] the global/local model was established, and the work pay attention to the continuity of the physical properties around the cross-sectional area of the interface Figure 3&4.
Figure 3:Detail of the Macro-homogeneous multi-layer model.
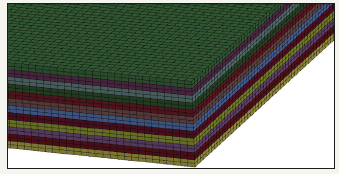
Figure 4:Individual steps of the creation of the Mesoheterogeneous model: single yarn (a), woven fabric (b), multi-layer composite plate with matrix (c) and final assembly with the projectile pictured from the above (d).

However, the numerical simulations of ballistic impact damage are seldom conducted based on the microstructure level. Tabiei & Ivanov [32] implemented micro-mechanical material model into the LSDYNA to discount the shear moduli and accounted for reorientation of the yarns. Gu [33] presented a microstructure model to simulate the penetration process of 3D braided composites, which obtained that the residual velocity played a role in the energy absorption and damage of the composite. Karkkainen [34,35] established RVEs of 2D and 3D woven textile and developed cohesive element failure model to explore progressive failure of composites. The mechanical properties of the 3D braided composite tubes depend largely on them preform structures, such as yarn orientation, yarn curvature, and fiber volume fraction. Hence, many researchers payed large attention on the simulation of tubes.
Fatigue Failure
Due to the three-dimensional integrated braided preform structure, 3D braided composites have higher interlamination shear strength and damage tolerance than laminated composites [2,3]. The fatigue deformation and failure of 3D braided composite are the important mechanical behaviors for braided composite materials under long-time services. The geometric model of 3D braided composites can be divided into three types: fatigue life models, phenomenological models and progressive damage models.
Wu et al. [36] discussed the stress distribution of 3D braided composite and fatigue damage mechanisms were analyzed. From such an investigation, the fatigue behaviors could be optimized. developed a microstructure geometrical model under three-point low-cyclic bending fatigue to research the stress distribution and deformation of fiber tows and resins. Feng et al. [37] found that fatigue damage starts from the elements of contact area between the fiber bundles, and then it spreads to the surface and interior of fiber bundles.
Summary and Prospect
This paper mainly introduces the research progress of prediction of strength, low-velocity impact and fatigue failure of 3D braided composites. Based on the analysis and comparison of the existing strength criterion, the finite element model was established, and its strength was calculated. Meanwhile, the damage mechanism of 3D braided composites under impact was explored by changing yarn orientation, yarn curvature and fiber volume fraction. The fatigue properties of 3D braided composites are also discussed. But 3D braided composites for extreme conditions (mainly including low and high temperature environment) on the mechanical properties and the influence of time factor of research work is lacking. In addition, scholars mainly of 3D braided composites at low speeds damage under impact load is studied, under the action of the high-speed impact and explosive loads the mechanical behavior of research is less. Therefore, the research scope and depth of 3D braided composites need to be expanded. Due to its high specific strength and stiffness, especially its integrity, anti-stratification, anti-impact and designability, 3D braided composites will be widely used in aerospace, military industry, ships, sporting goods, transportation and architecture, and become one of the most widely used materials.
Acknowledgments
This work was supported by the National Nature Science Foundation of China [grant numbers 11602160,11402160,21501129]; the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi [grant number 2017117]; and the opening foundation for state key laboratory for strength and vibration of mechanical structures [grant number SV2017-KF-01, SV2019-KF-01]; and the “1331project” Key Innovation Teams of Shanxi Province.
References
- Hosur MV, Jeelani S (2005) Manufacturing and low velocity impact characterization of foam filled 3D integrated core sandwich composites with hybrid face sheets[J]. Compos struct 69(2): 167.
- Hashin Z (1980) Failure criteria for unidirectional fiber composites. Journal of Applied Mechanics 47(2): 329-334.
- Puck A, Schürmann H (1998) Failure analysis of FRP laminates by means of physically based phenomenological models. Composites Science & Technology 62(12):1633-1662.
- Chang FK (1987) A Progressive damage model for laminated composites containing stress concentration. Journal of Composite Materials 21(9): 834-855.
- Hill R (1948) A theory of the yielding and plastic flow of anisotropic metals. Proceedings of the Royal Society of London 193(1033): 281-297.
- Hoffman O (1967) The brittle strength of orthotropic materials. Journal of Composite Materials 1(2): 200-206.
- Tsai SW (1971) A general theory of strength for anisotropic materials. Journal of Composite Materials 5(1): 58-80.
- Sun HY, Qiao X (1997) Prediction of the mechanical properties of threedimensionally braided composites. Composites Science & Technology 57(6): 623-629.
- Gu B (2004) Prediction of the uniaxial tensile curve of 4-step 3-dimensional braided preform. Composite Structures 64(2): 235-241.
- Zi LU (2002) Numerical prediction of strength for 3d braided composites. Journal of Beijing University of Aeronautics & Astronautics 28(5): 563- 565.
- Zeng T, Wu LZ, Guo LC (2004) A finite element model for failure analysis of 3D braided composites. Materials Science & Engineering A366(1): 144-151.
- Zeng T, Wu LZ, Guo LC (2004) Mechanical analysis of 3D braided composites: a finite element model. Composite Structures 64(3): 399- 404.
- Karkkainen RL,Sankar BV (2006) A direct micromechanics method for analysis of failure initiation of plain weave textile composites. Composites Science & Technology 66(1): 137-150.
- Karkkainen RL, Sankar BV, Tzeng JT (2007) A direct micromechanical approach toward the development of quadratic stress gradient failure criteria for textile composites. Journal of Composite Materials41(9): 299-318.
- Karkkainen R, Tzeng JT (2009) Micromechanical strength modeling and investigation of stitch density effects on 3D orthogonal composites. Journal of Composite Materials 43(25): 3125-3142.
- Song S, Wass MA, Shahwan KW, Xiao X, Omar F (2007) Braided textile composites under compressive loads: Modeling the response, strength and degradation. Composites Science & Technology 67(15): 3059-3070.
- Song S, Wass MA, Shahwan KW, Xiao X, Omar F (2015) Compression response of 2d braided textile composites: single cell and multiple cell micromechanics-based strength predictions. Journal of Composite Materials 42(23): 2461-2482.
- Dong JW, Feng ML (2010) Asymptotic expansion homogenization for simulating progressive damage of 3D braided composites. Composite Structures 92(4): 873-882.
- Dong J, Feng M (2010) Damage simulation for 3d braided composites by homogenization method. Chinese Journal of Aeronautics 23(6): 677- 685.
- Zhang C, Xu X, Mao C (2011) Progressive damage simulation and strength prediction of 3D braided composites. Acta Materiae Compositae Sinica 28(2): 222-230.
- Hao W, Yuan Y, Yao X, Ma Y (2015) Computational analysis of fatigue behavior of 3D 4-directional braided composites based on unit cell approach. Advances in Engineering Software 82(C): 38-52.
- Li XK, Liu Z, Hu L, Wang Y, Lei B, et al. (2017) Numerical investigation of t-joints with 3D four directional braided composite fillers under tensile loading. Applied Composite Materials 24(1): 1-21.
- Zhang D, Li C, Sun Y, Zhang Y, Qian Y (2017) Multi-scale modeling of an integrated 3d braided composite with applications to helicopter arm. Applied Composite Materials 24(5): 1-18.
- Xiao X, Kia HG, Gong XJ (2011) Strength prediction of a triaxially braided composite. Composites Part A 42(8): 1000-1006.
- Lei B, Liu Z, Ya J, Wang Y, Li X (2016) Bearing abilities and progressive damage analysis of three dimensional four-directional braided composites with cut-edge. Applied Composite Materials 23(4): 839-856.
- Wang Y, Lei B, Liu Z, Li X, Huang X (2017) Investigation on the bearing abilities of three-dimensional full five-directional braided composites with cut-edge. Applied Composite Materials 24(4): 1-18.
- Hao W, Wang Y, Lei B, Liu Z, Li X (2017) A unit-cell model for predicting the elastic constants of 3d four directional cylindrical braided composite shafts. Applied Composite Materials 25(3): 619-633.
- Heimbs S, Brouke BV, Kergomard YD, Dau F, Malherbe B (2012) Rubber impact on 3d textile composites. Applied Composite Materials 19(3-4): 275-295.
- Elias A, Laurina F, Kaminskia M, Gornet L (2017) Experimental and numerical investigations of low energy/velocity impact damage generated in 3D woven composite with polymer matrix. Composite Structures 159: 228-239.
- Bresciani LM, Manesa A, Ruggiero A, Iannitti G, Giglio M (2016) Experimental tests and numerical modelling of ballistic impacts against Kevlar 29 plain-woven fabrics with an epoxy matrix: Macrohomogeneous and Meso-heterogeneous approaches. Composites Part B: Engineering 88: 114-130.
- Rao MP, Nilakantan G, Keefe M, Powers BM, Bogetti TA (2009) Global/ local modeling of ballistic impact onto woven fabrics. Journal of Composite Materials 43(5): 445-467.
- Tabiei A, Ivanov I (2002) Computational micro‐mechanical model of flexible woven fabric for finite element impact simulation. International Journal for Numerical Methods in Engineering 53(6): 1259-1276.
- Gu B (2007) A microstructure model for finite-element simulation of 3D rectangular braided composite under ballistic penetration. Philosophical Magazine 87(30): 4643-4669.
- Karkkainen RL (2015) Dynamic micromechanical modeling of textile composite strength under impact and multi-axial loading. Composites Part B. 83: 27-35.
- Karkkainen RL (2015) Dynamic micromechanical modeling of textile composite strength under impact and multi-axial loading. Composites Part B. 83: 27-35.
- Wu L, Zhang F, Sun B, Gu B (2014) Finite element analyses on threepoint low-cyclic bending fatigue of 3-D braided composite materials at microstructure level. International Journal of Mechanical Sciences 84: 41-53.
- Jiqiang F, Xinfeng W (2018) Fatigue life prediction of 3-d four-directional braided composites. Journal of Nanjing University of Aeronautics & Astronautics 50(1): 45-52.
© 2018 Zhangxin Guo. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






