Evolution of Engineering Acoustic Waves with Metamaterials

The control of acoustic waves have critical applications across many fields, including ocean geology, [1] marine biology, [2] and biomedical engineering. [3] Controlling the direction and dissipation of acoustics waves plays a critical role in noise cancellation [4,5], ultrasonic imaging, [6] and many other applications. Acoustic metamaterials play a significant role in the development of technology used to control acoustic waves. Acoustic metamaterials have interesting properties that interact with incoming pressure waves in unique ways. In particular, these metamaterials are able to exhibit a negative bulk modulus. [7] Contradictory to our natural intuition (nature materials with positive bulk modulus), a negative bulk modulus refers to an increase in volume from an external compressive force [8]. This negative bulk modulus phenomenon occurs at some particular frequency range near monopolar resonance. When acoustic metamaterials are subjected to an oscillating signal near the resonance frequency too fast for the medium to respond in time, a phase shift can be observed. This phase shift impliesπ that the response signal is the negative of the incoming signal. Due to this phase delay, the volume of the metamaterial unit cells responds in a negative manner in respect to the oscillating pressure field, resulting in negative bulk modulus [8]. Similar effects can be observed for mass density subjected to dipolar resonance in which the delay in response causes the center of mass of each unit cell to decelerate when pushed by the oscillating pressure field. In the frequency range where the monopolar and dipolar frequency ranges overlap, the metamaterial exhibits both negative bulk modulus and negative density. The effects of these two negative material properties result in a negative phase velocity with a negative refractive index.

Unlike nature materials, the properties of metamaterials result from the resonance of designed unit cells. It was initially thought that these resonators would need to have dimensions on the same order of magnitude as the signal wavelength. [9] In this case, creating acoustic metamaterials for high frequency signals seemed feasible, but impractical for low frequency signals. In 2000, Dr. Ping Sheng’s group demonstrated how to design an array of metamaterial elements having sizes two orders of magnitude smaller than the signal wavelength. [7] These individual unit cells have a high density center composed of lead surrounded by silicon. [7] Transmitting a signal near monopolar resonance resulted in the detection of an object exhibiting a negative bulk modulus due to the phase delayed response of the metamaterial.

Research done by Dr. Xiang Zhang’s group in 2006 demonstrated that certain structures can also exhibit a negative bulk modulus. [8] The structures were Helmholtz resonators with dimensions much smaller than the signal wavelength. In Zhang’s experiment, the resonators were aligned in a series within a square aluminum tube serving as an acoustic waveguide. When these resonators [8] were excited near monopolar resonance, the structure was observed to have a negative bulk modulus. [8] This research demonstrated the new- found versatility of metamaterials. Now it was known that metamaterials were not strictly materials, but also structures with similar resonance characteristics. Because the phase velocity through a medium is calculated by the square root of the bulk modulus divided by the density, it was questioned if having a negative bulk modulus or negative density would have a similar effect on the phase velocity. Mathematically, a negative bulk modulus or negative density both result in a purely imaginary phase velocity. Physical realization of this imaginary phase component illustrated a rapid wave decay through propagation. In other words, the metamaterial exhibits a frequency band gap where acoustic waves cannot propagate when either the bulk modulus or density is negative, but not both. The question remains on the realization of negative phase velocity. To achieve this goal, we need to get back to the formulation of the phase velocity given by , where is the bulk modulus and is the mass density of the medium. Without loss of generality, we express the bulk modulus and inverse of density in their complex forms and = with K0, , , and being the magnitude and phase of the corresponding quantities. If K< 0 and < 0, we have and , which yield

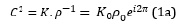
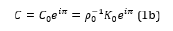
Thus, the phase velocity is negative when both bulk modulus and density are negative (Figure 1), and so is the acoustic refractive index of the metamaterial inversely proportional to the phase velocity.

figure 1:

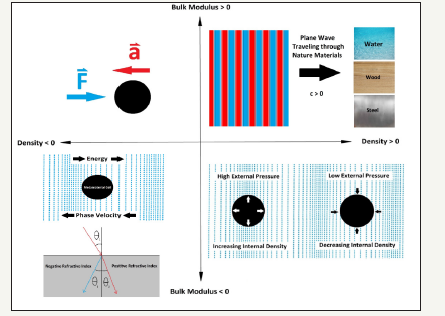
Material properties of medium where acoustic Figure 1. waves propagate. For all nature materials, both density and bulk modulus are positive, resulting in positive phase velocity and refractive index. For metamaterials with monopolar/dipolar resonance, negative bulk modulus/density can be observed near the resonance, respectively. Negative bulk modulus or density but not both results in a purely imaginary phase velocity and a frequency bandgap where acoustic waves cannot propagate in the metamaterial. Only when both the bulk modulus and density are negative will the phase velocity be negative, indicating that the acoustic wave front propagates in the opposite direction of the energy flow inside the medium.

The experimental realization of a negative phase velocity and refractive index is achieved in an experiment by Dr. Thomas Brunet. [10] This experiment explored the overlap of monopolar and dipolar resonances range with soft silicon microbeads suspended in a water-based gel, resulting in simultaneous negative bulk modulus and negative density. [10] When these two attributes are combined, the phase velocity becomes negative as derived in Eq. (1). Meaning that the phase of the wave front travels in the opposite direction of waves propagating through nature materials.

Now that the fundamental physics of a negative bulk modulus, negative density, and negative refractive index have been discovered, waves having zero refraction index and infinite phase velocity became intriguing. Research done by Zhang’s group demonstrated the physical realization of this concept with the development of metamaterials with simultaneous zero mass density and infinite bulk modulus. [11] This is achieved with a two-dimensional acoustic waveguide confined by two parallel plates with scattered areas of low effective phase velocity [11]. The low phase velocity areas are realized with an array of cylindrical indents in both parallel plates [11]. This structure achieved infinite phase velocity and zero refractive index at some certain frequency.

With these foundational experiments establishing the fundamental physics of metamaterials, scientists and engineers have focused on the applications of these fascinating media. The goals of metamaterial development focus on the control of acoustic and phononic transport in unconventional ways [12]. Later studies illustrate the potential applications of metamaterials. These includes invisibility cloaking, [13,14] directional noise cancellation, [4,5] subwavelength ultrasonic medical imaging,6 architectural acoustic illusion, [15] and acoustic comprehensive sensing [16]..

1. Badiey M, Cheng AH, Mu, Y (1998) From geology to geoacousticsevaluation of biot-stoll sound speed and attenuation for shallow water acoustics. The Journal of the Acoustical Society of America 103(1): 309- 320.
2. Au WW, Banks K (1996) The acoustics of snapping shrimp in kaneohe bay. The Journal of the Acoustical Society of America 99(4): 2533-2574.
3. Fink M, Montaldo G, Tanter M (2003) Time reversal acoustics in biomedical engineering. Annual Review of Biomedical Engineering 5(1): 465-497.
4. Fleury R, Sounas D, Alù A (2015) An invisible acoustic sensor based on parity-time symmetry. Nature Communications 6(1).
5. Zhu X, Ramezani H, Shi C, Zhu J, Zhang X (2014) PT-symmetric acoustics. Physical Review X 4(3).
6. Zhu J, Christensen J, Jung J, Martin L, Yin X, et al. (2010) A holeystructured metamaterial for acoustic deep-subwavelength imaging. Nature Physics 7(1): 52-55.
7. Liu Z (2000) Locally resonant sonic materials. Science 289 (5485): 1734-1736.
8. Fang N, Xi D, Xu J, Ambati M, Srituravanich, et al. (2006) Ultrasonic metamaterials with negative modulus. Nature Materials 5(6): 452-456.
9. Fok L, Ambati M, Zhang X (2008) Acoustic Metamaterials. MRS Bulletin 33(10): 931-934.
10. Brunet T, Merlin A, Mascaro B, Zimny K, Leng J, et al. (2014) Soft 3D acoustic metamaterial with negative index. Nat Mater 14(4): 384-388.
11. Dubois M, Shi C, Zhu X, Wang Y, Zhang X (2017) Observation of acoustic dirac-like cone and double zero refractive index. Nature Communications 8: 14871.
12. Cummer SA, Christensen J, Alù A (2016) Controlling sound with acoustic metamaterials. Nature Reviews Materials 1(3).
13. Zhang S, Xia C, Fang N (2011) Broadband acoustic cloak for ultrasound waves. Physical Review Letters 106(2).
14. Zigoneanu L, Popa B, Cummer SA (2014) Three-dimensional broadband omnidirectional acoustic ground cloak. Nat Mater13(4): 352-355.
15. Dubois M, Shi C, Wang Y, Zhang X (2017) A thin and conformal meta surface for illusion acoustics of rapidly changing profiles. Applied Physics Letters 110(15): 151902.
16. Xie Y, Tsai T, Konneker A, Popa B, Brady DJ, et al. (2015) Single-sensor multi speaker listening with acoustic metamaterials. Proceedings of the National Academy of Sciences 112(34): 10595-10598.