Stochastic Analysis of Random Heterogeneity of Bathymetry at Gulf of Mexico

Seafloor topography (bathymetry) is not well known compared to the land topography because our geodesy equipments, for example GNSS/InSAR, do not work below thick water. Our understanding of land surface of the Moon is better than the Earth’s ocean floor. However, importantly, the bathymetry influences ocean current [1], geology [2], heat flow [3,4] and biological diversity [5]. The bathymetry at the northern Gulf of Mexico has been measured very well because of the oil and gas production and its 3D seismic surveys.

The Bureau of Ocean Energy Management (BOEM) released the detailed bathymetry grid in 2016 (Figure 1a); [6]. The grid size is 12.1x12.1m2 (40x40ft2) and the bathymetry covers more than 230000km2. The average horizontal resolution of the bathymetry is roughly 15m, and the uncertainty of the depth is 1.3%. Because the resolution of a typical global model is around 900m (SRTM30_PLUS) [7] this BOEM grid has much higher lateral resolution. This grid provides us an interesting opportunity to study the detailed bathymetry and its relationship to various physical, chemical, and biological phenomena. The rough seafloor surface at -96W- -90W is prominent, and this deformation is largely due to the migration and dissolution of the deep salt deposits [8]. This structure is stopped at the Sigsbee Escarpment, where the south end of the colored topography area is in Figure 1a. Another slope on the east side, which is smoother, is called West Florida Escarpment. In the middle (right west of Box III), the Mississippi canyon exists, which was created by the Mississippi river when the sea level was low. I use a stochastic approach similar to [9] to understand the random heterogeneities of the ocean floor in Figure 1a. For a random medium, anisotropic autocorrelation functions can represent the stochastic nature of the medium [10]. This approach has been used to numerically model the bathymetry with different characteristic functions [11,12].

I select three areas (I, II and III) and compute the 2D Fourier transform and power spectra density function (PSDF) of them (Figure 1b,1c & 1d). The bright color (high power) indicates the highly heterogeneous media. Interestingly, the directions of heterogeneity vary at different locations. In Areas I and II, ocean topography is heterogeneous in the NW-SE and NE-SW directions, respectively. In Area III, the topography has no preferential directions. I speculate that this pattern in Area III is due to the loop current entering through the Yucatan Channel [13]. The size of Area III is large and contains different directions of heterogeneities.

Figure 1:Bathymetry of Gulf of Mexico Colored area [6] (Figure a). The background gray image shows the bathymetry provided by ETOPO2. The boxes represent the areas used for the stochastic analyses. The size of Boxes I and II is 170x242km2 and for Box III 145x182km2 (Figure b, c & d). The power spectra density of the random heterogeneities at each box in Panel (Figure a) and the top-left Roman numbers indicate the location. The axes are in the logarithmic scale, and hence the data points of wave number 0 are not shown.

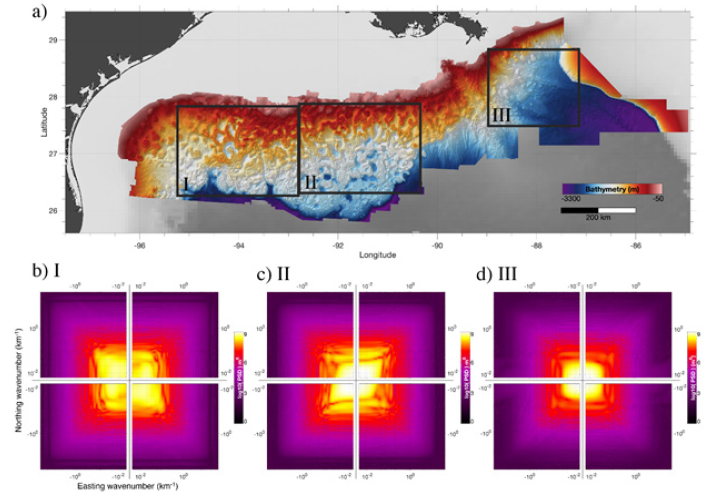
When I fit the PSDF using von Karman model, I can measure the autocorrelation length of the randomness, which represents the randomness [14,15]. In Area I, because the medium has anisotropic randomness, two autocorrelation lengths are important, and the short and long lengths are 9 and 25km, respectively. Area II is also anisotropic, and short and long lengths are 17 and 50km, respectively. This means that Area I contains finer structure than Area II. Area III can be represented well by an isotropic random medium with the autocorrelation length of 50km. Overall, the salt dissolved area at the north of the Sigsbee Escarpment has small-scale heterogeneities than eastern areas. The random characteristics of bathymetry estimated here should be compared to other data such as geology, ocean current, geo and ocean-chemistry and biology. The fins-scale bathymetry grid is a unique opportunity to study local-scale correlations between them[16].

1. Kunze E, Smith SGL (2004) The role of small-scale topography in turbulent mixing of the global ocean. Oceanography 17(1): 55-64.
2. Rodolfo KS (1969) Bathymetry and marine geology of the Andaman basin and tectonic implications of southeast Asia. GSA Bulletin 80(7): 1203-1230.
3. Parsons B, Sclater JG (1977) An analysis of the variation of ocean floor bathymetry and heat flow with age. Journal of Geophysical Research 82(5): 803-827.
4. Zhong S, Ritzwoller M, Shapiro N, Landuyt W, Huang J, et al. (2007) Bathymetry of the pacific plate and its implications for thermal evolution of lithosphere and mantle dynamics. Journal of Geophysical Research 112(18): B06412.
5. Koslow JA (1997) Seamonts and the ecology of deep-sea fisheries. American Scientist 85(2): 168-176.
6. (2016) BOEM Northern gulf of Mexico deep-water bathymetry grid from 3d seismic. BOEM, USA.
7. Becker JJ, Sandwell DT, Smith WHF, Braud J, Binder B, et al. (2009) Global bathymetry and elevation data at 30arc seconds resolution: SRTM30_Plus. Marine Geodesy 32(4): 355-371.
8. Aharon P, Roberts HH, Snelling R (1992) Submarine venting of brines in the deep gulf of Mexico: Observations and geochemistry. Geology 20(6): 483-486.
9. Nakata N, Beroza GC (2015) Stochastic characterization of mesoscale seismic velocity heterogeneity in long beach, California. Geophysical Journal International 203(3): 2049-2054.
10. Ishimaru A (1978) Wave propagation and scattering in random media. Academic Press Inc, USA.
11. Goff JA, Jordan TH (1988) Stochastic modeling of seafloor morphology: Inversion of sea beam data for second-order statistics. Journal of Geophysical Research 93(B11): 13589-13608.
12. Goff JA, Jordan TH (1989) Stochastic modeling of seafloor morphology: A parameterized Gaussian model. Geophysical Research Letters 16(1): 45-48.
13. Chiri H, Abascal AJ, Castanedo S, Antolinez JAA, Liu Y, et al. (2019) Statistical simulation of ocean current patterns using autoregressive logistic regression models: A case study in the Gulf of Mexico. Ocean Modelling 136: 1-12.
14. Sato H, Fehler MC, Maeda T (2012) Seismic wave propagation and scattering in the heterogeneous Earth: Second Edition. Earth Sciences & Geography, Switzerland.
15. Sato H (2019) Power spectra of random heterogeneities in the solid earth. Solid Earth 10(1): 275-292.
16. Leipper DF (1970) A sequence of current patterns in the Gulf of Mexico. Journal of Geophysical Research 75(3): 637-657.