Development of Volume Function for Final Felling of Pinus brutia Ten in Kurdistan Iraq

Forests are considered as important assets in the economy of any country. They provide a variety of natural resources such as food, raw material, fuel wood and fodder. Other benefits of forests include the provision of landscape for recreational opportunities, protection of soil against erosion, purification of water, production of oxygen, consumption of carbon dioxide, regulation of microclimate and provision of biological diversity. The industrial revolution and high demand of forest products during the 19th century resulted in a substantial deforestation that caused a reduction in the extent of the world total forest area from 50% to 30% [2]. An alternative approach is establishing for new forest plantation for timber, fuel wood and pulp and paper production and existing natural forests are mainly for conservation and protection purposes [2]. As a result, fast-growing tree species such as, Acacia, Pinus and Eucalyptus have been a popular choice of species planted in forest plantation worldwide [3]. According to Yasodha et al. [4], about 48% of the overall forest plantation worldwide is aimed at industrial use; 26% for agro forestry, fuel wood, soil and water conservation and the remaining 26% of other purposes that have not been specified. Thus, there is an increasing demand for forest plantation to and to full fill the increasing demand for forest products [5]. In the recent years, due to high demand for forest products resulting from rapid development in technology, the focus of governments and private sectors have been on mass reforestation programmers with fastgrowing industrial tree species with the intention to shorten the rotation cycle and fulfilling the increasing demand of the timber market.

In 1988, the Iraqi Ministry of Agriculture had planted about 30 hectares of Pinus brutia Ten in the mountainous area of Zawita by using a planting space of 3x3m. Pinus brutia Ten is a natural species to Zawita area, which is located in the north western part of Kurdistan region, and extending to far north of Iraq. The region ranges between 800 to 1600 meters in altitude. The species has a considerably tolerance to poor soils, frost and draught. This species is planted not only in Kurdistan region, but also in other parts of Iraq. The species is easily adapted to different climates and conditions of the region. The species was selected for the study because it has an economic importance. Its wood is used for fuel wood, pulp and charcoal. This species is considered a lightdemanding. Tree volume equation is useful for forestry practices in estimating the volume to be harvested based on certain parameters like tree diameter and height that can easily be measured. Such method has been used for more than a hundred years West et al. 2009. But the information from commercial tree plantation is lacking in most developing nations. They are simple methods and tools that can be used to estimate either individual tree volume or the volume of the entire forest plantation stands. Volume equations have been studied for many years and continuously attracting many researchers in the field of forestry.

It is being researched and studied widely because there are no single volume equations that can be satisfactorily used for all tree species [6,7] and no single model suitable for all purposes [8,9]. The lack of the technical information on forests in the Zawita region is one of the main obstacles to the continuation and development of standards and environmental policy in the area. The forest plantation evaluation in Zawita needs more scientific work on the development of yield models [10]. According to Department of Forest, University of Duhok, Iraq, the development of yield models for this species growing under Kurdistan Region will contribute towards providing valuable information in planning and sustainable management of the forest plantations in the region. This work has been carried out to develop volume functions for brutia P Ten that can demonstrate the relationship between tree volume and diameter and provide a useful tool in managing Zawita forest in future. The specific objectives of this study are:- to develop volume functions for brutia P Ten based on dbh and dbh and height; to compare the goodness-of-fit of potential volume function of Pinus brutia Ten by using Furnival’s Index (FI); and to recommend the best fit equation of Pinus brutia for Zawita area in Kurdistan.

Sample plots

Figure 1: (a) Map of Iraq (b): Map of the Duhok Province (c): Map of Zawita.

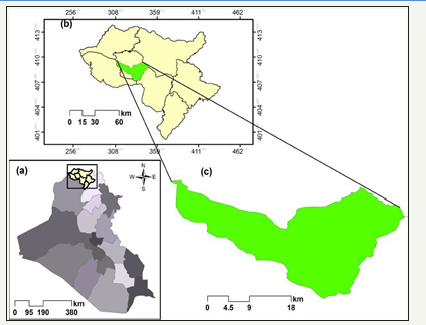
Figure 2: Illustration of 10 point sampling design [11].

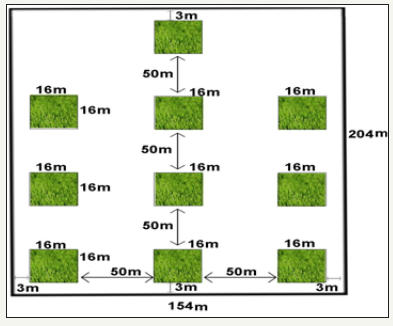
Naturally, P brutia ten grows in Zawita area, which is located in the north western part of Kurdistan region, and extending to far north of Iraq as shown in (Figure 1). The area usually receives about 724.5mm mean annual precipitation (meteorological station in Zawita for the period 2010-2014). The region ranges between 800 to 1600 meters in altitude. The species is considered to be tolerant to poor soils, frost and draught. This study area is characterized by clay soil as a result of the fragmentation of the ancient rocks. Zawita forests are exposed to harsh climatic conditions where there is a huge contrast in temperature and the amount of rainfall received during the year. During winter, rain and snow fall occur in the region and the amount of the rainfall in the past five years exceeded to 215mm. Every year, the relative humidity was recorded highest in January. In 1988, the Iraqi Ministry of Agriculture planted about 30 hectares of P. brutia ten in the mountainous area of Zawita by using a planting space of 3x3m. In this study, 3 hectares (204 x 154m) plot was established and the plot consists of (250-300) trees. We used 10 point sampling Design [11] as showed in (Figure 2), in our study. For data collection, first, we randomly selected the starting point of sampling in the 3-hectare-plot. In the second stage, we systematically selected 9 quadrates and each quadrate is (16 x 16m). Each quadrate has equal-distance of 50m horizontally and vertically. Then we selected trees in each plot randomly for felled, standing and validating trees. For example, in first plot for felled trees we chose the first tree and all other trees we wrote in a paper then we mixed a paper and randomly chose other tree .Thus for all plots, we repeat the procedure. Table 1 shows the number of trees in each plot for felled, standing and validation.

Table 1:The number of trees in each plot.

Felled trees

Prior to felling, the base diameter (0.3m above ground level) (Comment: bas diameter is the correct term to us. I have not come across the term before) and the diameter at the breast height (DBH- 1.3m above ground level) of each selected tree were measured. The following measurements were also taken after felling:-

a. Total height in meter.

b. Merchantable height in meter (up to 10cm diameter over bark of the main stem).

c. Diameter over bark at 3m intervals along the stem length and at its mid-point (1.5m intervals).

d. Bark thickness (cm) at each point of diameter measurement.

All diameters were measured by using a diameter tape and bark thickness was measured using a bark-gauge. As a whole, 76 felled trees were measured.

Standing trees

The base diameter and diameter at breast height were measured by using a diameter tape. As for standing trees, the same measurements as in felled tree were taken. A total of 150 standing trees were measured.

Validation tress

Diameter was measured at every 20% of trees merchantable height. Means we divided tree to 5 sections, each section was 2 meters in order not to get bias. Because of inherent morphological differences among tree species. A total of 44 validation trees were measured

Volume calculation

The calculation of volume of each section of felled and standing trees was performed using Newton’s formula, so that both overbark and under-bark volumes were calculated for felled trees, whereas only over-bark volumes were calculated for standing trees.

The formula was used for log sections with three diameter measurements. The volumes of felled tree sample and standing tree sample were calculated by using the following formula.

1. Volume over bark

Figure 3:

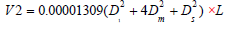
2. Volume under bark

Figure 4:

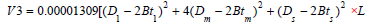
Where V2 is the volume over bark, V3 is the volume under bark, L is the Length of the log section, D1 is the diameter at the large end of the log section, Dm is the diameter at the mid-point of the log section, Ds is the diameter at the small end of the log section, Bt1 is the bark thickness at the large end of the log section, Btm is the bark thickness at the mid-point of the log section and Bts is the bark thickness at the small end of the log section. For both felled and standing trees, the volume of individual section will be added to the total tree volume up to 10cm diameter.

Descriptive analysis was carried out for both felled and standing trees to find mean, standard deviation, and range of DBH, merchantable height, total tree height, merchantable volume over bark for both felled and standing trees, and merchantable volume for felled trees. Table 2, illustrates the results of descriptive analysis.

Table 2:Summary of parameters measured and calculated (Pinus brutia Ten). Based on Newton’s formula and volume was up to 10cm diameter over bark.

In forestry literature, there are plenty of mathematical models which have been used by various authors in the construction of volume-tables and volume equations [12,13], while recent developments in this area were reported by [14-22]. In most cases, those models were found to be suitable for use in specific forests. In this study, we selected 15 models to compare with each other in order to find the most suitable ones for the species. We used the method of least squares for the construction of volume equation because the most common problem in volume table construction has been the heteroscedasticity of residuals. This is because the larger tree volumes tend to deviate from the regression line more than the smaller ones. Cunia et al. [23] proposed the use of weighted least squares to correct the heteroscedasticity in volume table construction. We also used both weighted and un-weighted equations to fit the model. For the over bark volume equation, we used both felled and standing trees data. However, for under bark volume equations, we only used the felled trees data.

Un-weighted equations

In this study we used eight un-weighted volume equations, as displayed in (Table 3). In the table, D is the DBH (cm), H is the total log length (m) from the ground to up 10cm over bark, and V is the merchantable volume (m3).

Table 3:Show the regression model un-weight volume equations.

Weighted equations

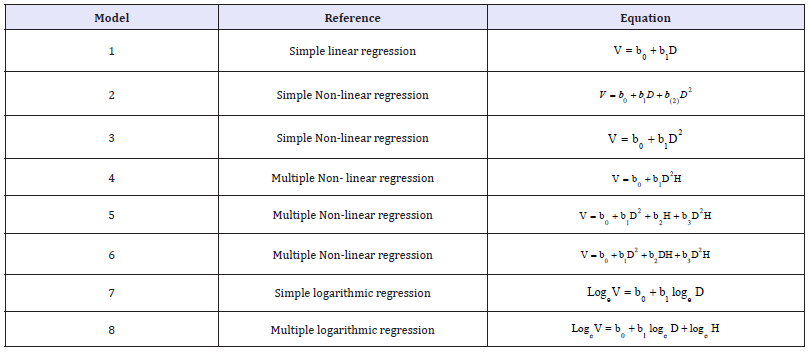
Cunia et al. [23] argued that using the logarithms of tree volume equations was not the best option to surmount the problem of heterogeneity of variance. One important drawback of this method is that by taking logarithms, the estimation of the arithmetic mean is automatically replaced by the estimation of the geometric mean. Since the first one is always larger than the second one, the results are definitely biased. Alternatively, the common technique used to overcome the non-homogeneity of the variance in tree volume construction is the weighted least squares. A common weight factor for volume that uses both variable predictors D and H is1/(D2H) , since the variance of stem volume tends to increase in proportion to D2H as reported by Furnival’s & Wright et al. [24,25]. In this study, seven weighted volume equations, as displayed in (Table 4) were used. It must be noted that equations 15, 17, and 19 are divided by D2H, and other equations are divided by D2 (V, D, and H in weighted volume equations as defined).

Table 4:Show the regression models weighted volume equations

Furnival’s Index

The precision of a regression equation is usually measured by using the statistics such as coefficient of determination (R2). However, these statistics do not take into account other factors like heterogeneous variance. A more suitable index for comparison of regression equations has been developed by Furnival et al. [24], which is based on the concept of maximum likelihood. Furnival’s index value increases the large residuals, departures from linearity, non-normality and heterogeneous variance. Thus a decrease in its value indicates an improved fit to the data. However, Cunia & Wright et al. [23,25] illustrated the need of weighted volume equations in order to equalize or to induce homogeneity of variance in volume along the regression line. This would be the pre-requisite before validity test of significance that can be applied to the regression equation. Transformed models or the inclusion of weighted values into the analysis posed problems in testing the goodness of fit in selecting the most suitable model. Regression models goodness of fit cannot be compared directly by using the coefficient of determination R², R² adjusted, and MSE when the same dependent variables in the models are subjected to different weightings or transformations. In practice, the regression model may be biased by weighting or a transforming of the dependent variable, which in this case is volume. To compare such regression equations, a more suitable index is the expression of Furnival et al. [24], which is given as follows:

Figure 5:

In the equation above, FI is Furnival’s index, (f´ (V))-¹ is the geometric mean of the derivative of the dependent variable with respect to volume, and s is the residual standard deviation from the fitted regression. The geometric mean of the derivatives of the dependent variable V of the un-weighted regression is a number, while the derivatives of the dependent variables V/D²H, V/D², and Loge V of the weighted equations are D²H, D², and V respectively. In this study, the best fitted regression was indicated by the equation with the smallest Furnival’s Index. The derivative of the dependent variable V of the un-weighted equations was 1.

The derivatives of the dependent variables V/D2 and V/D2H of the weighted equations were D2 and D2H respectively. The geometric means were obtained by using the formulae below:

1. Geometric mean D2 = antilog (Σ logD2 )/n

2. Geometric mean D2H = antilog (Σ logD2H)/n

According to Meyer et al. [18], Lárus Heiðarsson 2014, the calculated volume per tree obtained from a logarithms volume equation is affected by a systematic error which is introduced when taking the antilogarithm of Log₁₀ V . This error can be approximately corrected by multiplying a logarithmic equation by a factor as follows: If common logarithms are used in the volume equation, the correction factor is:

Figure 6:

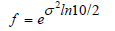
Where f is the tree volume correction factor, σ2 is the logarithms error variance, and In 10 is the natural logarithm of 10 (≃2.3026). If natural logarithms are used in the volume equation, the correction factor is;

Figure 7:

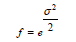
Where e is approximately 2.718282 and σ2 is as above.

Regression analysis includes the estimation of parameters, assessing the regression coefficients, calculating the coefficient of determination (R2), standard error of estimation, and checking the important assumptions of regression analysis using the histogram and scatter plot of residuals. These were conducted using statistical analysis software SPSS version 22, as well as the descriptive analysis including mean, standard deviation, minimum, and maximum of the collected data. For calculating the geometric mean and Furnival index and figuring the merchantable volume table, the statistical analysis software R version 3.1.2 was used. The over bark and under bark merchantable volume tables, and the corresponding graphs were made by using the Microsoft Office Excel 2010. Regression analysis was carried out by using a commercial statistical package on a micro computer system. Further analysis was done to calculate the Furnival Index (FI). The equation with the smallest FI indicates the best fit regression for both weighted and un-weighted over bark.

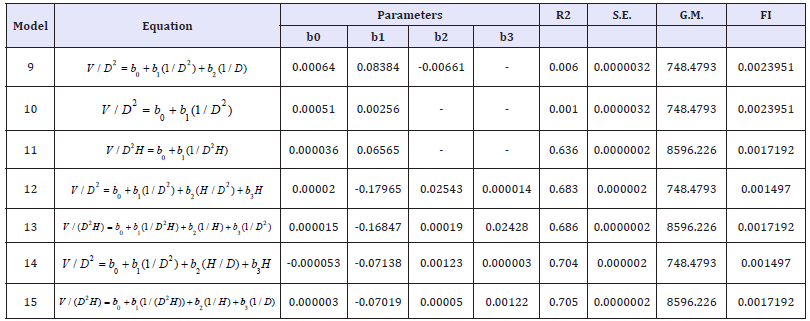
Descriptive analysis was carried out for both felled and standing trees, the equation with the smallest FI indicates the best fit regression for both weighted and un weighted over bark as shown in (Table 5a, 5b).

Table 5a:Un-weighted equations over bark volume.

*Equation 8 the best fit volume equation

Table 5b:Weighted equations over bark volume.

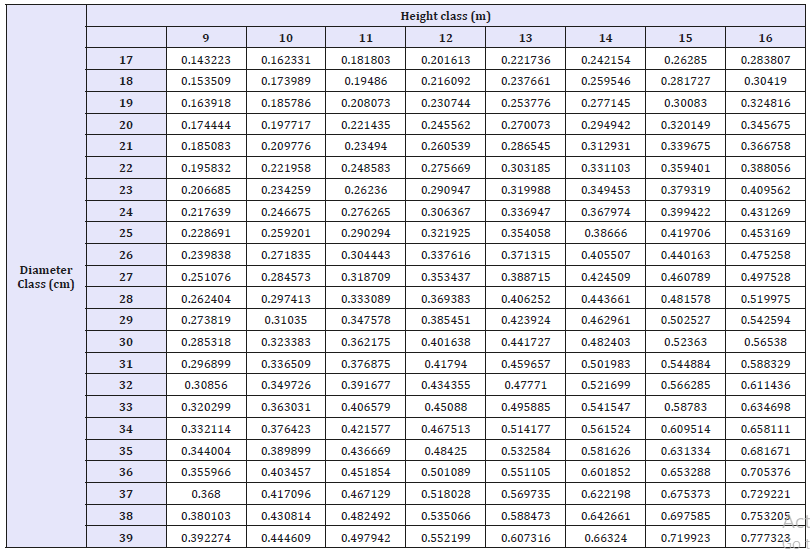
One way to assess the accuracy of a volume table is by comparing the calculated volume with the predicted volume (Table 6a, 6b). We found that the average over bark merchantable volume was 0.4058832m3, derived from the equation 8(VO =0.0002722* D^1.40425 * H^1.06470 ) compared to the true over bark merchantable volume of 0.39853m3 as shown in Table 7a. Similarly, the average under bark merchantable volume of 0.352308m3, drived from the equation 8 (VI =0.0003378 * D^1.21342 * H _1.18863 ) compared to the true over bark merchantable volume of , 0.355545m3 as shown in Table 7b.

Table 6a:Un-weighted under bark volume equations, *Equation 8 the best fit volume equation.

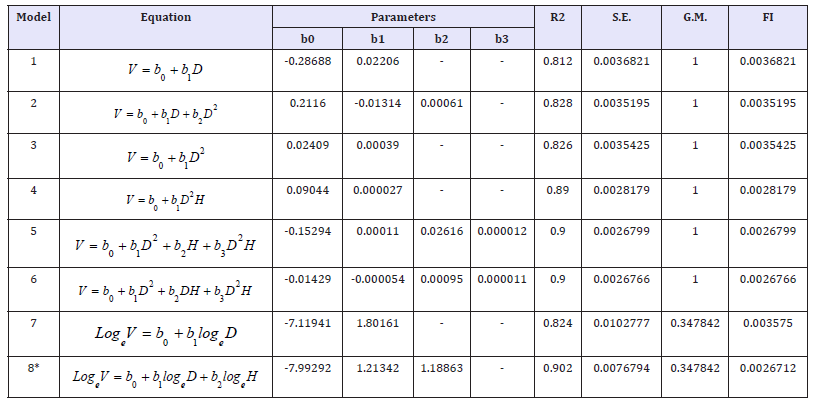
Table 6b:Weighted under bark volume equations.

Table 7a:The merchantable volume over bark (m3).

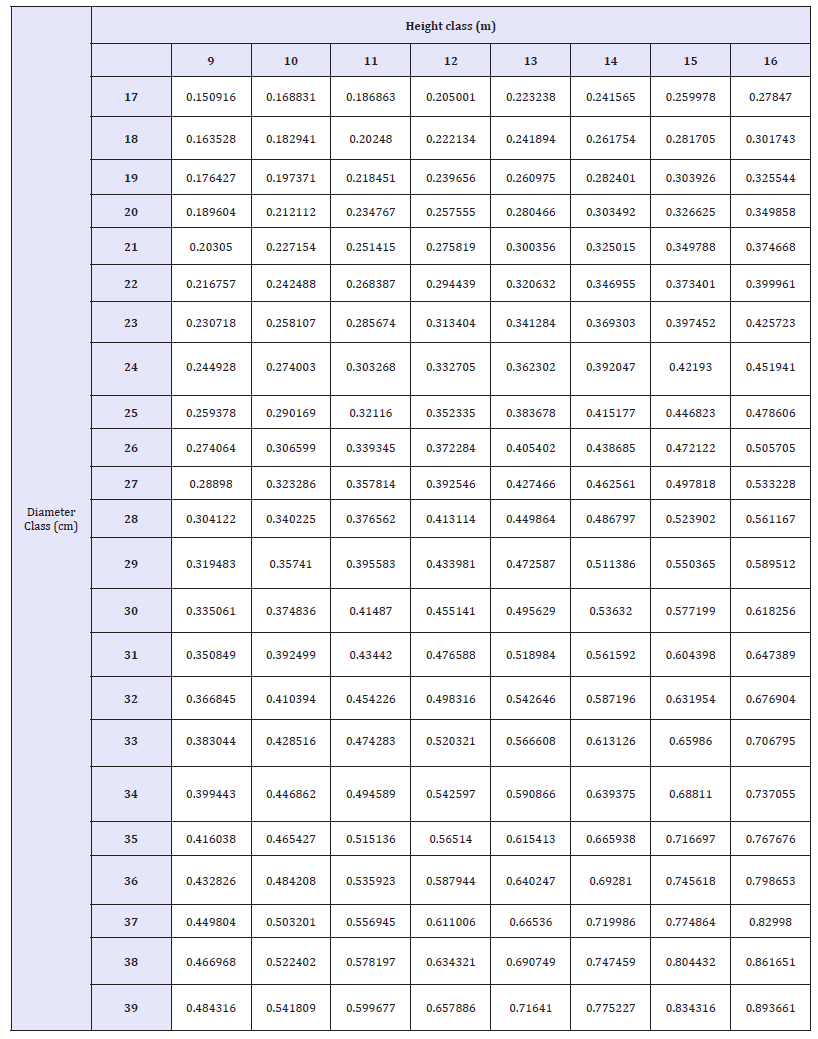
Table 7b:The merchantable volume under bark (m3).

In validation, the average over bark true merchantable volume was 0.459167m3, drived from the Newton’s formula and compared to 0.460784m3 estimated merchantable volume derived from the equation Vo =0.0002722* * , The true average merchantable volume under bark estimated using the Newton’s formula was 0.40211m3, compared to 0.404860 m3 the average estimated merchantable volume derived from model VI=0.0003378* D^1.21342 * H^1.18863 , (Table 8a and 8b).

Table 8a:Data validation for over bark volume of Pinus brutia Ten, bas on model regression 8.

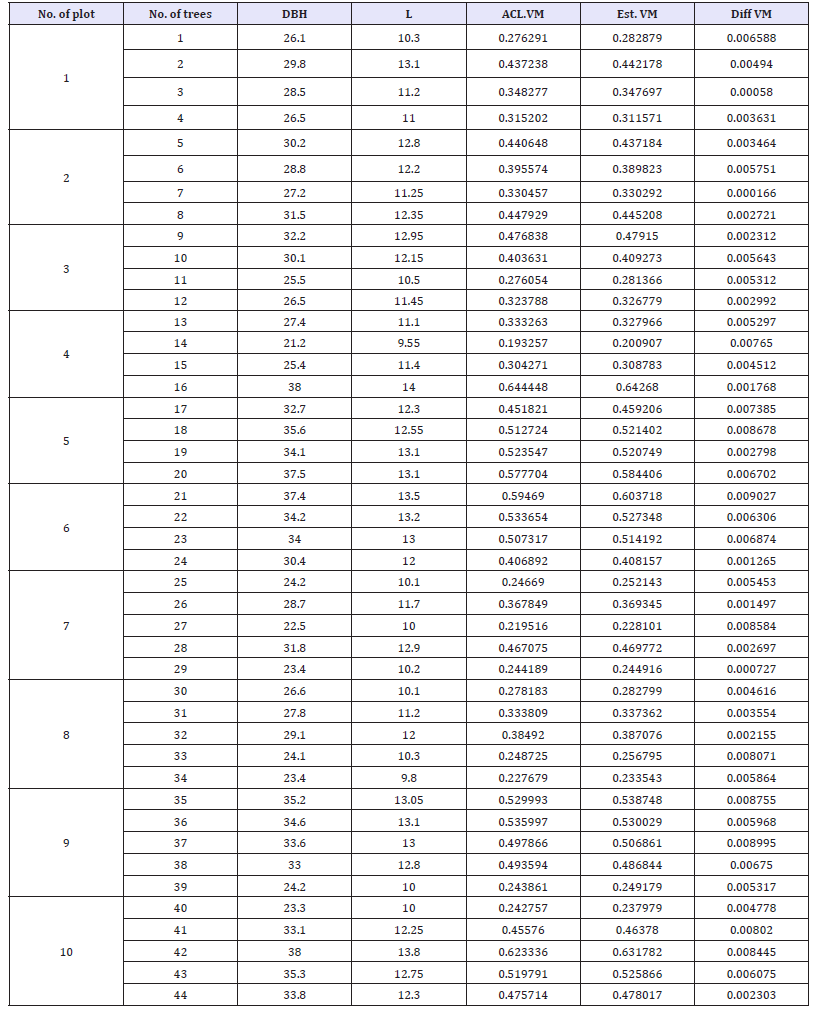
Table 8b:Data validation for under bark volume of Pinus brutia Ten, bas on model regression 8.

We used the least squares method to construct the volume equations. The data were fitted to both un-weighted and weighted volume equations, and we used the Furnival’s Index (FI) in order to fit the best model .Amongst fifteen individual tree volume models tested during the study, two models, with two estimated parameters, were judged as the best when bias and precision used as criteria to predict over-bark volume of Pinus brutia Ten. Both models for over and under bark volumes were a double-entry models that used for both diameter at breast height and height as independent variables as shown below:-

Over-bark volume equation: VI = 0.0003378 *D^1.21342*H^1.18863 Equation 8

Under-bark volume equation: VO =0.0002722* D^1.40425 *H^1.06470 Equation 8

Wan Razali et al. [18] used eight un-weighted and seven weighted equations (including two logarithmic). The method of least squares was used to fit volume equations and the best fit equations were selected by smallest value of the Furnival’s index for both over-bark and under-bark volume equations. The logarithmic equation, adjusted for bias, was chosen as the final equation to construct the over -bark and under-bark volume tables as follows:

V = 0.0003150 (D^1.54738 )(H^0.80931 ) and V = 0.0002707 (D^1.54738 )(H^0.80931 )

In our study for over bark volume equation the, R2 was 0.96, bias 0.0008, S.E 0.0035 and FI was 0.0013. For under bark equation the, R2 was 0.90, bias 0.0005, S.E 0.0076 and FI was 0.0026. In the study done by Wan Razali et al. [18], they selected the same models for over and under bark volume for Mangium which was a doubleentry model that used both diameter at breast height and height as independent variables. Nuray Misir et al. [20] used the Developing volume equation for Ash (Fraxinus angustifolia subsp Oxycarpa) in Turkey. The researcher selected 391 sample trees from stand in Turkey; Twenty-six equations were examined in order to select the best one. He applied V= b1DH+ b2D2H because it had a very high of coefficient of determination (R2=0.99) and a low standard error (SE=0.312m3), with two independent variables height and diameter at breast height (dbh) [26,27]. The research has similarity with our work because we also got equation with two independent variables with R2=0.968 and (SE=0.0035596m3). Our equation is better than this study because we selected the equation based on Furnival index and because we have both weight and un-weight volume equation not only R2 and SE and other hand the SE are better than Nuray Misir et al. [20]. Pesonen [28] this study aimed to develop growth and yields models for larch which was applied on growth and yield simulators and calculated the forest inventories in eastern Iceland. The Norrby’s model predicted the absolute true value for individual-tree volume than the others volume prediction models. For construction of the diameter increment model, data and models both were used. The ultimate aim of the construction of the prediction models was to know about the relationship between total tree height and diameter at breast height, dominant height and age, and future five-year diameter increment and tree and stand characteristics. Consequently, the Restricted Maximum Likelihood (REML) method was used to estimate the parameters of random parameter models. . To find the best fitting equations for modelled characteristics, numerous linear and non-linear model forms were tested during preliminary analyses.

Khamsene 2009 developed a volume equation to predict the tree volume and taper function and to describe a stem profile by using 73 Styrax tonkinensis trees in New Zealand. Amongst eighteen individual tree volume models tested for under bark volume estimation, they selected a double-entry model that used both diameter at breast height and height as independent variables (V=– 0.0011383579 0.000052703D2H–0.0000008312D2H2). Analysis of residuals showed that the model above was better than the all eighteen models. The statistics included bias (mean residual), the standard error of estimate (SEE), the standard deviation of the residuals (SDR) and mean absolute deviation (MAD). Similarly, Juntunen [29] the main objective of this study was to develop growth and yield models for lodge pole pine plantations in Iceland. The relationship between stem volume and height diameter and diameter increment were the modelled tree level characteristics whereas the relationship between the dominant height and age, and between the diameter distribution and natural self-thinning were the modeled plot level characteristics to be were: To differentiate the dominant height and stand mean height an additional model for possible data preparation was needed.

Yousefpour [30] used the volume equation and volume table of Pinus Pinaster Ait; and data were measured in Kiashahr region (north of Iran). The researcher used the volume equations based on one and two variables and consequently the result gave the smallest relative standard error for the set of data, of volume equation with two independent variables, logarithmic stem volume equation based on tree height, diameter at breast height (dbh), and on both variables was determined for Pinus Pinaster Ait. Wan Razali [31] the least squares method fitted the four un-weighted and five weighted volume equations to get the volume data of each of the two species groups: Dipterocarp Merantis - Dark Red Meranti (DRM) and Light Red Meranti (LRM) which were obtained from the mixed tropical forest of Malaysia. In this study, the criterion of Furnival’s Index (FI) was used to select the best fit regression equation of each species group. Finally, the homogeneity of variance in volume, along the regression lines were equalized by using a more superior method of the weighted least squares and then the Furnival’s Index as statistical measure of goodness-of-fit was used to validate it. Similarly, Heidarsson [32] The goal of larus study was to evaluate different types of volume and taper equations of three species Picea sitchensis , Picea abies and Picea glauca in Norway, which can be used to predict single-tree stem volume and stem diameter at any given height. Data from a total 617 sample trees were used, leastsquares method was used to fit regression model for the volume equation, for independent variables used (DBH) and (H) was gave a best result for validation and statistical.

In conclusion, it was found that the best volume equation (Equation 8) for under bark had a very small Furnival index (FI=0.002), with high coefficient of determination (R2=0.90) and a low standard error (SE=0.007). And for over bark the best volume equation (Equation 8) had a very small Furnival index (FI=0.001), with very high coefficient of determination (R2=0.96) and a very low standard error (SE=0.003). The residuals between predicted and observed volume values have shown a normal distribution for both equations. Although the study was conducted in a specific region, it is generally expected that the models of volume equations derived from the study will provide a satisfactory estimate of standing volume of planted P brutia ten in other regions.

1. Sharma M, Parton J (2007) Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology and Management 249(3): 187-198.
2. Kataria N, Yadav K, Kumari S, Singh N (2013) Micro propagation : An important tool for conserving forest trees. Pertanika Journal for Tropical and Agriculture Science 36(1): 1-26.
3. Borras SM, Franco J, Gómez S, Kay C, Spoor M (2012) Land grabbing in Latin America and the Caribbean. Journal of Peasant Studies 39(3-4): 845-872.
4. Yasodha R, Sumathi R, Gurumurthi K (2004) Micropropagation for quality propagule production in plantation forestry. Indian Journal of Biotechnology 3: 159-170
5. Kröger M (2012) Global tree plantation expansion: a review. Netherlands, p. 1-24.
6. Clutter JL, Fortson JC, Pienaar LV, Brister GH, Bailey RL (1983) Tim management: A quantitative approach. In: John Wiley & Sons, USA, p. 1-333.
7. Muhairwe CK (1999) Taper equations for Eucalyptus pilularis and eucalyptus grand is for the north coast in New South Wales, Australia. Forest Ecology and Management 113(2-3): 251-269.
8. Mc Clure JP, Czaplewski RL (1986) Compatible taper equation for loblolly pine. Canadian Journal of Forest Research 16(6): 1272-1277.
9. Cao QV, Burkhart HE, Max TA (1980) Evaluation of two methods for Cubic-volume prediction of loblolly pine to any merchantable limit. Forest Science 26(1): 71-80.
10. Akrawee ZM (2012) Criteria for evaluation the sustainable management and policy of Zawita forest in Duhok governorate north of Iraq. Mesopotamia Journal of Agriculture 40(2): 192-201.
11. Razali WM, Rosni M, Johani MZ (1983) Double entry volume table equations for some RRIM 600 Series clones of Hevea brasiliensis. Malaysian forester, New Zealand.
12. Spur SH (1952) Forest Inventory. Ronald Press Co. illus, New York.
13. Loetsch F, ZShrer F, Haller K, (1973) Forest Inventory, BLV Verlagsgesells chaft. Munich 2: 1-469.
14. Sadiq RA, Smith VG (1983) Estimation of individual tree volumes with age and diameter. Canadian Journal of Forest Research 13(1): 32-39.
15. Schreuder HT, Anderson J (1984) Variance estimation for volume when D2H is the covariate in regression. Canadian Journal of Forest Research 14(6): 818-821.
16. Green EJ, Strawderman WE (1985) The use of Bayes/empirical Bayes estimation in individual tree volume equation development. Forest Science 31: 975-990.
17. Meng CH, Tsai WY (1986) Selections of weights for a weighted regression of tree volume. Canadian Journal of Forest Research 16: 671-673.
18. Razali W, Khali Aziz, Chew TK (1989) A volume table for planted Acacia mangium in Peninsular Malaysia. Forest Science 2(2):110-121
19. Avery TE, Burkhart HE (2002) Forest measurements. In: McGraw-Hill (Ed.), Processing of laser scanner data algorithms and applications. ISPRS Journal of Photo grammetry and Remote Sensing, New York, USA, pp. 1-480.
20. Nuray Misir, Mehmet MISIR (2004) Developing double-entry tree volume table for ASH in Turkey. Kafkas Üniversitesi. Artvin Orman Fakültesi Dergisi 3(4): 135-144.
21. Ounekham K (2009) Developing volume and taper equations for Styrax tonkinensis in Laos, UC Research Repository, New Zealand.
22. Hjelm B (2011) Taper and volume equations for poplar trees growing on farmland in Sweden. Swedish university of agricultural sciences. Department of energy and technology 29(2): 1-47.
23. Cunia T (1964) Weighted least square method and construction at volume tables. Forest Science 10(2): 180-191.
24. Furnival GM (1961) An index for comparing equations used in constructing volume tables. Forest Science 7(4): 337-341.
25. Wright HL (1964) An investigation into the weighting of volume table equations, Dept of Forestry, University of Oxford, UK.
26. Meyer HA (1994) Internal communication, A correction for a systematic error occurring in the application of logarithmic volume equation. The Pennsylvania State Forest School Research Paper Number, pp. 7-30.
27. Razali W, Aziz K, Chew TK (1989) A volume table for planted Acacia mangium in Peninsular Malaysia. Forest Science 2(2): 110-121.
28. Pesonen A (2006) Modeling the Growth and Yield of Larch in Hallormsstaður, Iceland.
29. Juntunen M (2010) Modeling tree and stand characteristics of lodge pole pine Pinus contorta plantations in Iceland. University of Eastern Finland, Europe, pp. 1-68.
30. Yousefpour M, Fadaie KF, Fallah A, Naghavi F (2012) Volume equation and volume table of Pinus Pinaster Ait .International Research Journal of Applied and Basic Sciences 3(5): 1072-1076.
31. Wan Razali WM (2013) Development of standard volume equations for Malaysian timber trees i: dark red and light red merantis tropical agricultural science. Pertanika J Trop Agric Sci 36: 31-46.
32. Heidarsson L (2014) Volume and taper equations for Sitka spruce Picea Sitchensis Carr. Norway spruces Picea abies (L.) Karst and White spruce Picea glauca (Moench) Voss in Iceland.