- Submissions

Full Text
Determinations in Nanomedicine & Nanotechnology
A Study about Exothermic Chemical Reactor by ASM Approach Strategy
Akbari MR1*, Sara Akbari2 and Esmaeil Kalantari2
1Department of Chemical Engineering and Civil Engineering, Iran
2Department of Chemical Engineering, Iran
*Corresponding author: Akbari MR, Department of Chemical Engineering and Civil Engineering, Iran
Submission: February 24, 2020;Published: March 17, 2020

ISSN: 2832-4439 Volume2 Issue1
Abstract
In this paper, our aims are accuracy, capabilities and power at solving set of the complex non-linear differential at the reaction chemical. As all experts know most of engineering actual systems behavior in practical are nonlinear process and analytical scrutiny these nonlinear problems are difficult or sometimes impossible. Our purpose is to enhance the ability of solving the mentioned nonlinear differential equations at chemical engineering and similar issues with a simple and innovative approach which entitled “Akbari-Sara’s Method” or “ASM”.
Introduction and Theatrical Formulation
In this literature, we have set nonlinear differential equations governing of kinetic the plug reactor to chemical reaction [1,2], that can be investigated and resolved response and the actual reactions at reactors for scientists and engineers is very important, because they know the real answer for analysis and design of reactors against chemical reactions are important and highly sensitive in of executive tasks are created. Other methods compared to ASM do not have this ability to gain the solution of the presented problem in high precision and accuracy so nonlinear differential equations such as the presented problem in this case study should be solved by utilizing new approaches like AGM, Akbari Ganji Method [3-8]; (Figure 1). We consider a well-mixed continuous stirred tank reactor with the reaction and set of nonlinear differential equations. parameters F(the flow rate), CA0 (the initial molar concentration) , TA0 (the initial temperature),Q (the rate of heat input to the reactor), V(the volume of the reactor), E, ΔH, k0 (the pre-exponential constant reaction), cp and ρ denote the heat capacity and density of the fluid in the reactor.
Figure 1: A comparison between ASM and Numerical solution for concentration and temperature.

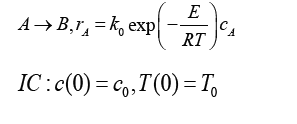
Set of nonlinear differential equations as follows:>
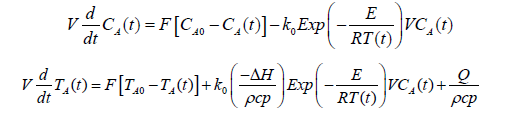
The solution of the mentioned problem by ASM will be obtained as follows:
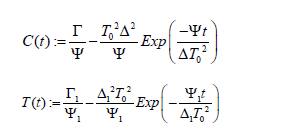
The following new variables are introduced as:
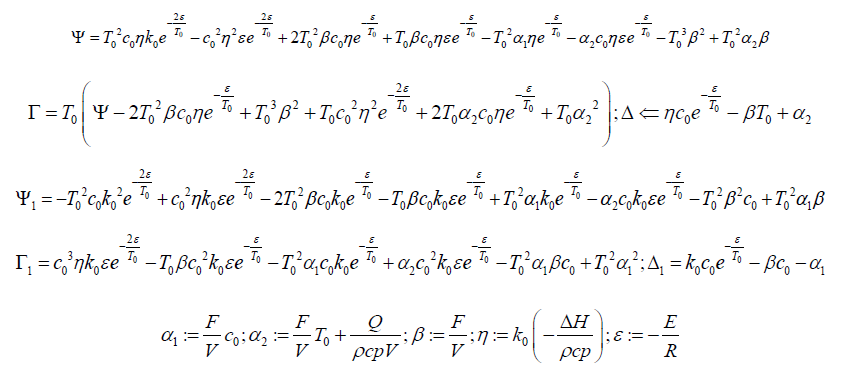
By selecting the physical values at below:
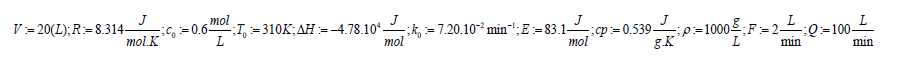
The solution is rewritten as follows:
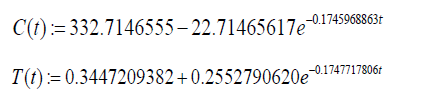
Acknowledgement
ASM and AGM (Akbari-Sara’s Method and Akbari-Ganji Methods) have been invented mainly by Mohammadreza Akbari (MR kbari) in 2019 and 2014 respectively in order to provide a good service for researchers who are a pioneer in the field of nonlinear differential equations. It is worthy to note that I am really grateful to all those who encouraged me to devise these methods which are highly beneficial for analytical solving coupled nonlinear ODEs (especially ASM) in Engineering, basic Sciences and Economic.
References
- Smith JM. Chemical engineering kinetics. Book Chemical Engineering Series 209: 74-99.
- James JC. Book chemical engineering series. University of Notre Dame, USA.
- Akbari MR, Ganji DD, Nimafar M, Ahmadi AR (2014) Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Frontiers of Mechanical Engineering 9: 390-401.
- Rostami K, Akbari MR, Ganji DD, Heydari S (2014) Investigating Jeffery-Hamel flow with high magnetic field and nanoparticle by HPM and AGM. Cent Eur J Eng 4(4): 357-370.
- Akbari MR, Ganji DD, Majidian A, Ahmadi AR (2014) Solving nonlinear differential equations of vanderpol rayleigh and duffing by AGM. Frontiers of Mechanical Engineering 9: 177-190.
- Ganji DD, Akbari MR, Goltabar AR (2014) Dynamic vibration analysis for non-linear partial differential equation of the beam-columns with shear deformation and rotary inertia by AGM. Development and Applications of Oceanic Engineering (DAOE).
- Akbari MR, Ganji DD, Ahmadi AR, Sayyid HHK (2014) Analyzing the nonlinear vibrational wave differential equation for the simplified model of tower cranes by (AGM). Frontiers of Mechanical Engineering 9(1): 58-70.
- Akbari MR, Nimafar M, Ganji DD, Akbarzade MM (2014) Scrutiny of non-linear differential equations Euler Bernoulli beam with large rotational deviation by AGM. Frontiers of Mechanical Engineering 9: 402-408.
© 2020 Baidoo Philip. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






