- Submissions

Full Text
Determinations in Nanomedicine & Nanotechnology
About the Interaction of Nanoparticles
GSolomon I Khmelnik*
Department of Fuel-Free Energy, Israel
*Corresponding author: Solomon I Khmelnik, Department of Fuel-Free Energy, Israel
Submission: December 13, 2019;Published: January 08, 2020

ISSN: 2832-4439 Volume1 Issue4
Abstract
Nanotechnology operates with nanoparticles, which has a distinct border with the environment. Practice shows that the interaction forces of such particles should significantly exceed the forces of intermolecular interaction, and the interaction can be both attraction and repulsion. Such interactions between nanoparticles are explained below on the basis of the solution of Maxwell’s equations.
Introduction
Nanotechnology operates with nanoparticles, which are an isolated solid-phase object
that has a clearly defined boundary with the environment, the dimensions of which in all
three dimensions are from 1 to 100 nm. Nanoparticles are close to those objects that are
considering in supramolecular chemistry [1]. In this field of knowledge, the forces that bind
individual molecules are considered. It is believed that intermolecular interaction consists of
weak electromagnetic interactions. The energy of such interactions is inversely proportional
to the sixth power of the distance between the molecules. Obviously, the interaction of
nanoparticles with clear boundaries cannot be due to such forces [2-4].
The interaction of nanoparticles leads to one property that greatly interferes with their use
- they can stick together [5-10]. This problem has to be solved in the production of ceramics
and metallurgy. Obviously, this property is explained by the attraction of nanoparticles with
different chemical compositions. But another property is also known, which can be explained
by the repulsion of nanoparticles with different chemical compositions. It was shown that
polycationic organic nanoparticles are shown to disrupt model biological membranes and
living cell membranes at nanomolar concentrations [2]. Thus, the theory of interaction of
nanoparticles should explain both the attraction and repulsion of nanoparticles, and the
forces of such interaction should significantly exceed the forces of intermolecular interaction.
The Maxwell equations for a capacitor with an alternating voltage in Cartesian coordinates
were solved [3]. In the system of Cartesian coordinates x, y, z, t and in the SI system these
equations have the form (1): (Table 1).
where Er, Eφ, Ez are the electric intensities, Hr, Hφ, Hz are the magnetic intensities? It was shown in [3] that this solution has the form:
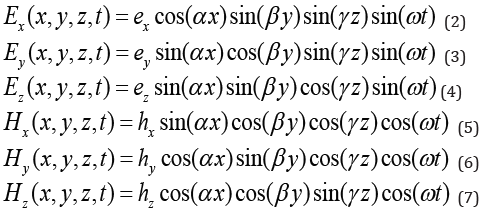
where ex, ey, ez, hx, hy, hz are the constant amplitudes of the intensities, α, β, λ are constants, ω is the frequency. These quantities are related by the following equations:
hz = 0(8)
Table 1:

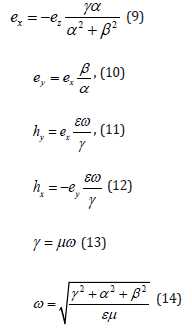
For given values of the parameters α, β, γ and frequency ω, the amplitudes of the intensities can be determined depending on ez. It follows from (14) that for ω = 0 the parameters α = β =γ = 0 i.e. the electromagnetic field cannot be static.
In (3) it is shown that energy with a density is stored in a capacitor
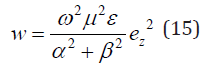
In this case, the density of energy fluxes along the coordinates are determined by the formulas
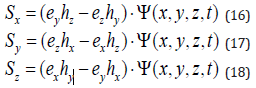
where
This means that the energy flux density along all axes varies in space and time, i.e. in a rectangular body there is a spatial standing wave. However, a stream of energy can pass through this body. Consider, for example, the face xoy at z = z1. The energy flux density (18) on this face is determined by function (19):
The energy flux is determined by the integral of this function on the entire xoy face:
The energy flux on the opposite face xoy at z = z2 is determined by the integral
From (18,20,21) we find the energy flux flowing through the capacitor along the 0z axis if (z2 < z1 ) :
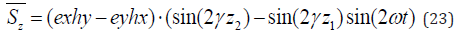
It Follows from the Solution Found that
A. There is a combination of parameters in which the
energy of the capacitor is not radiated. Consider, for example,
a cube with parameters α = β = λ . If the length R of the cube’s
half-edge is such that (α ⋅ R) = 0,sin(β ⋅ R) = 0,sin(γ ⋅ R) = 0 , then all the
energy flux densities on the faces of the cube are zero-cm. [2-7]. In
this case, there is no radiation.
B. An external energy flow can pass through the capacitor
volume without changing its internal energy (as shown above).
This flow is the active power that passes through the capacitor.
C. The formulas are valid for any values of μ and ε.
Therefore, a capacitor with a certain energy and a standing wave in
the capacitor volume can exist in a vacuum.
D. In the absence of external energy flows, the capacitor
retains its integrity, since it does not radiate, and the energy density
is preserved while maintaining the shape-see (15).
E. From p.p. 3 and 4 it follows that in some body, and even
in a vacuum, a keeper of energy and information can exist. This is
considered in detail in [3,4]. It is also shown there that a standing
electromagnetic wave possessing the above properties can have a
very diverse form.
F. Now suppose the nanoparticle stores the indicated
electromagnetic wave. Such a single nanoparticle. In the absence
of external energy flows, it retains its shape and electromagnetic
energy.
G. Suppose a portion of external energy was expended to
combine two nanoparticles. Then this portion of energy will go into
the energy of the combined nanoparticle. We call this portion the
binding energy of the conglomerate of two nanoparticles. Thus, the
energy of a conglomerate of two particles is greater than the sum of
the energies of these particles. Consequently, the conglomerate is
more stable than individual particles, because for the destruction
of the conglomerate it is necessary to first apply the binding energy.
This can explain the adhesion of nanoparticles (as discussed above).
Obviously, the binding energy of particles for different materials is different. Now suppose that two particles of different materials come together and a conglomerate of these particles forms. If these materials do not mix, then conglomerate 21 should enter the environment of conglomerates 1 or 2. Obviously, it will enter the environment of conglomerates 1 if the binding energy of material 1 is higher than the binding energy of material 2. This can explain the above-mentioned fact that organic nanoparticles can destroy living cells.
References
- Shanefield DJ (1995) Organic additives and ceramic processing. Kluwer Academic Publ, Boston, USA.
- Leroueil PR, Hong S, Mecke A, Baker JR, Orr BG, et al. (2007) Nanoparticle interaction with biological membranes: Does nanotechnology present a Janus face? Accounts of Chemical Research 40(5): 335-342.
- Khmelnik SI (2019) Inconsistency solution of Maxwell’s equations. Mathematics in Computer Corp, pp. 1-240.
- Khmelnik SI (2019) Electromagnetic keeper of energy and information. Canadian Journal of Pure and Applied Sciences 13(2): 4853-4859.
- Sameerah I, Saeedi A, Laila H, Rahman A, Ahmed MAD, et al. (2018) Catalysts. 8(452): 1-14.
- Laila H, Rahman A, Ahmed MAD, Mohamed SSA, Samar KH (2016) Catal Lett 146: 1373-139.
- Rahman A, Ahmed MAD, Rafat MEK, Shaimaa MAF (2016) J Bioorg Chem 69: 140-152.
- Ahmed MAD, Mahmoud WS (2017) Mater Res Express 4: 035039.
- Ibrahim EMM, Ahmed MAD, Elshafaie A, Ahmed AM (2017) Materials Chemistry and Physics 192: e41-e47.
- Ahmed MAD, Mahmoud WS (2018) Journal of Physics and Chemistry of Solids 116: 375-385.
© 2020 Solomon I Khmelnik. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






