MINT-Wigris Environment and Tool Bag

In the handbook are described teaching units for a course on the deuteron atomic kernel. Beside the 8 models a teacher can stick together like molecules in a chemistry tool bag, there is theory added in several articles on the Tool bag, G-compass, dark energy, matter, whirls, dihedrals, energy and the 6-roll mill, gluon exchange, handcrafts, the octahedron and spin.
In this article I repeat from older publications my view on Einstein metrics. In the article on Planck units https.//en.wikipedia.org/wiki/Planck units you find that quantum effects are not incorporated into general relativity and a quantum gravity theory does not exist. This is false. The author published that already years ago in the MINT-Wigris articles which are not reviewed by Wikipedia. The Figure 1 shown is a bubble in space and deuteron has its own inner 4-dimensional space and dynamics. This is a SU (3) geometry projection of the strong S5 sphere geometry which is projective normed to a complex 2-dimensional space CP² with a bounding Riemannian sphere S². The S² sphere is divided up in six polar hemisphere caps with input-output vectors in the center for energy exchanges between the deuteron and its environment. The hedgehog caps are obtained from the S² by the parity operator which identifies diametrical opposite points p, -pεS² such that the hemisphere is a projective space P².

Figure 1: Deuteron atomic kernel model with two nucleons, 6 quarks, gluon exchange in the nucleons between paired quarks and rgb-graviton spin-like vectors on the black marked x-, y-, z-space axes.

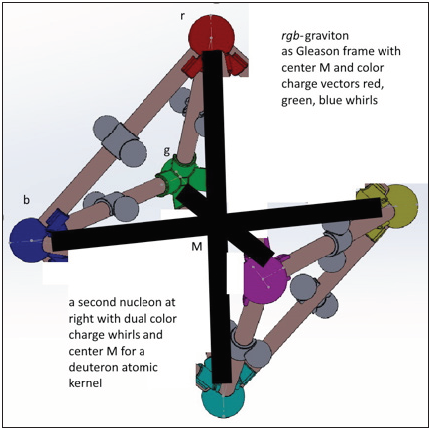
There are two caps poles for exchanges and measures of Higgs mass and speeds v for momentum p=mv with which AK moves in its environment. The internal cos Θ rescaling of mass is through the special relativistic factor. It arises through the special relativistic speed between barycentrically, spherical coordinates generated by the strong interaction in AK and Euclidean coordinates generated by the weak interaction isospin exchange between paired u-. d-diquarks on an x-or y-or z-axis. As computed for matter waves, this cos Θ speed is then the speed of momentum p. The energy transfer is via the Einstein formula mc²=hf in a projective P² space which has beside the mass-frequency plane a loop/circle S1 at projective infinity. Instead of P² the geometry can also be a Klein bottle where two Moebius strips are joined at their boundaries. This introduces Minkowski metric in the quantum range. It adds up for local special relativistic coordinates of systems in the large (Figure 2-7).

Figure 2:Minkowski watch.

Figure 3:Hedgehog with six caps P² for the electrical, magnetic, kinetic, rotational energies, heat and gravity/mass energy. On these P² the change from an input to an output vector (or reversely) occurs.

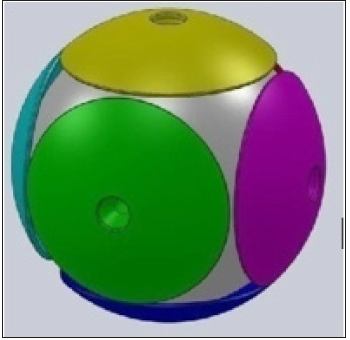
Figure 4:The Moebius strips are a subspace of P2; the Gleason frames below generate projective Gleason operators in P3.

Figure 5:There is a Gleason frame 123 assumed which carries the 3 masses of neutral leptons similar to a spin whose vectors carry length; spin/ magnetic momentum is on the top vertex of the hanging tetrahedron, momentum on the bottom vertex; neutral charge is on the left unmarked vertex.

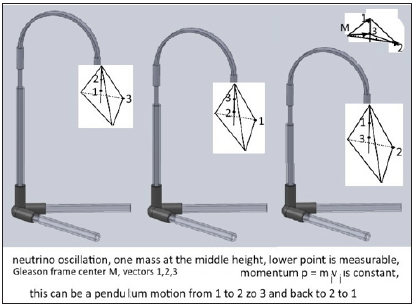
Figure 6:Fano memo.

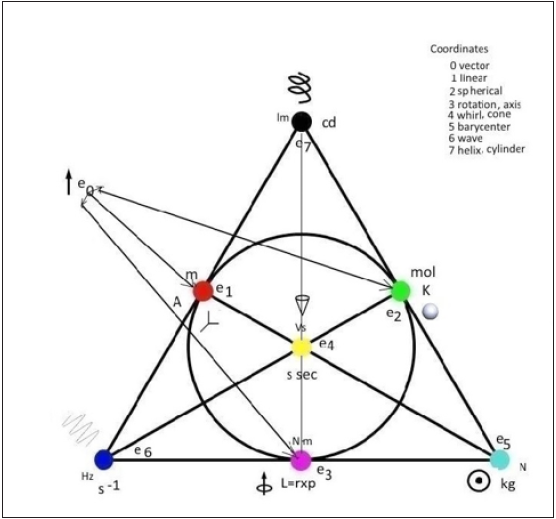
Figure 7:Hedgehog, spiralic roots for length contraction.

The rgb-graviton whirls are superpositions of three QCD color charge whirls red, green, blue and can decay into phonons for heat which transfer momentum (blue) and energy as scaled heat (green, use the Boltzmann constant). The gravity induction is obtained through the cross product of the rgb-graviton vector with mass vectors, carrying the three quarks Higgs mass as measure in kg. In contrary to an EM charge, rescaling of the mass scalar is allowed. For including general relativity, it is observed that the ud-diquarks weak isospin exchange means the center B of the AK mass is slightly moving and not one fixed point. A Schwarzschild radius Rs of AK is generated with center B inside. AK measures its distance towards a quarks mass center Q as |BQ|=r, r radius. A quark measures its distance unsymmetrical as |QB|=r- Rs. Projective geometrical these are two different coordinates. In a central projection the image in a plane for the B,Q with tip B and Q sitting between the plane and B has a homogeneous normed scaling factor (r-Rs)/r, the general relativistic metrical rescaling cos²β with sin²β = Rs/r. Both Einstein metrics have an area invariance as length/time lt = l‘t‘for special relativity and in the tangent space differentials rescaled metric dr∙cdt = dr‘cdt‘. The general relativistic rescaling adds up for a star P rotating about a central sun Q and adds after one revolution a fixed phase angle for the nearest point between Q, P as a gravitational acceleration of the P speed.

This quantum gravity theory uses the Einstein computations unchanged; it includes no computation for Rs. From the matter wave rescaling above the Minkowski metric can be derived by using the Minkowski orthogonal rescaling projection in (Figure 2). Orthogonality belongs to projective geometry where projection operators split the space into two parts, orthogonal to one another. The polar complex coordinates of a plane do this by transferring Euclidean z=x+iy coordinates through x=rcos φ, y=rsin φ into polar coordinates with angle φ and radius r. Affine geometry of Einstein has to be projective extended.
This quantum gravity theory of MINT-Wigris claims that it has an induction like the EM electromagnetic induction between electrical charges and magnetic fields and momentum: The EM cross product triple can be repeated for gravity in atomic kernels AK from deuteron on. Beside the Higgs field which sets the mass scalars like a charge there are the color charge whirls superpositions introduced and called rgb-gravitons, - for nucleons in AK which extend the nucleon quark triangle
3-dimensional to a tetrahedron. Two of them are joined at the new tips B of their tetrahedron as in Figure 1. Higgs sets a deuteron ‘s slightly moving barycenter point. It is pointed out that different spaces, different dimensions, geometries, transformation symmetries and measuring operators are needed to accommodate the modern findings in the nano range of nucleons. The gluon strong interaction space has the 8 dimensions of its symmetry SU (3). The geometry is a toroidal product of a 3-dimensional sphere with a 5-dimensional sphere. For the projection of the S³ onto the Hopf sphere S³ of the weak interaction’s symmetry SU (2) the first three Gell-Mann SU (3) matrices are used. They present a superposition of the three-color charges red r, green g, blue b as a rgb-graviton whirl and are a spin-like Gleason frame which spans with the 3 vectors endpoints a nucleon triangle with 3 quarks as vertices. The two nucleon tetrahedrons for deuteron are shown in Figure 1. They have the Gleason frames center in common. Beside the 8-dimensional projection of the SU (3) geometry into Euclidean space the dynamics adds time. There are several rotors inside CP², partly described in the handbook’s articles. For the weak interactions 4-roll mill a weak tetrahedron can be constructed having at its vertices an electrical or neutral charge, a magnetic momentum with spin at one vertex (use the gyromagnetic relation), the mass of electrical charged leptons and a kinetic energy location at the fourth vertex. It is not seen as the momentum of these leptons, but as induction which lets the electrical charge rotate on a latitude circle of the Hopf sphere S². For neutral leptons the helicity shows momentum diametrical (equal or) opposite to the magnetic/spin vector.
In the introduction to this article the Planck units are mentioned. They belong to the big bang W for the universe. Often such a big bang is described as a point at infinity from where the universe and its energies developed. As first coordinates after W are mentioned that a coordinate vector for length, named e1 a real octonian/Euclidean x-coordinate is generated, also heat as octonian coordinate e2 a polar complex angle or octonian/Euclidean y-coordinate for a real plane R² and third time t, scaled as r=ct for a radius r as length, c speed of light. This octonian coordinate e4 carries also magnetic energy. Electrical charge is measured on e1. The first particles mentioned are quarks which carry beside their EM electrical charge mass (an octonian coordinate e5) and have as geometrical retract a lemniscate with two foci for mass and EM. MINT-Wigris postulates that they are located in a black hole substuting W and a radius inversion at the Schwarzschild radius of the new W expands them 3-dimensional, adding an octonian/Euclidean space coordinate e3 or spherical angle θ. It allows a flow rotation inside a brezel of genus 2 for the quark and carries rotational energy with angular speed ω and sets angular momentum. For rotations the conjugation operator C of physics adds a rolled Kaluza-Klein circle U (1) as S1 as octonian e8 coordinate. It introduces the map φ→exp(iφ) for the use of the exponential, polar complex function. C sets also with its dihedral D1 symmetry the clockwise cw and counterclockwise mpo rotations on S1. From single quarks which decay by the use of the weak interaction WI are generated nucleons having 3 quarks confined in a volume by the strong interactions SI gluon exchange. The real cross product generates the third space coordinate and as symmetry the quaternions of WI. The rgbgravitons are a Gleason frame measure which attributes to them the three color charges red, green, blue of SI. This and single-color charges are whirls like spin or magnetic flow quanta. They can change in an up-down position for input-output vectors. On the 2-dimensional hemispheres as polar caps of a nucleon’s hedgehog (Figure 7) surface S² such energy vectors can be located. They turn in a time cycle on a Moebius strip by a 360-degree rotation. The parity P operator acts on S² for the factor space P² by identifying diametrical opposite points p, -pεS². The Moebius strip is inside P² available. Setting vectors, vector addition and vector fields in spacetime needs an additional octonion coordinate e0 which sets also energy units. The time reversal operator T can be used for this. It adds for travelling waves for instance their wavelength. For oscillations between two fixed endpoints of a string it reverses the expansion and the integer numbered wavelength has to fit to the string’s length. Building atomic kernels from nucleons, dinucleons in a deuteron are generated. Between the paired six u, d-quarks on a Euclidean axis is a weak isospin exchange with a decaying u-quark releasing a weak W+ boson which is absorbed by its partner d-quark. The former d-quark is then a u-quark and the former u-quark is left as a d-quark after the decay. The WI and SI exchanges have different speeds. In order to make the atomic kernel stable a rescaling of mass according to the Minkowski metric (Figure 2) is necessary. This is introduced through an orthogonal projection operator due to the Higgs mass m setting operator. It allows to set the Schrodinger matter wave equation travelling with a speed v<c in its environment [1,2]. As new octonion coordinate, bifurcating from e5, is generated e6. This coordinate carries momentum p=mv for the atomic kernel. From speed v=Δx/Δt is bifurcating frequency f=Δt for the e6 coordinate. The 8 octonion coordinates have another multiplication than the SI 8 gluon matrices λj of SU (3). They allow in addition to th SI rgb-graviton and the spin Gleason frames GF seven such GF, shown in the Fano memo as seven lines each containing 3 points for their 3 frame vectors. The λj are 3x3-matrix extended from the three Pauli matrices σi of the WI SU (2) symmetry by inserting a row and a column with coordinates 0. These 9 projection matrices project a complex 3-dimensional space down to a complex 2-dimensional space. In addition, the σ3 extended ones are linearly dependent and generate only two λj for gluons. The SI geometry is a toroidal product of two spheres S³xS5 and the Hopf WI geometry S³ has a fiber bundle structure with fiber S1 and image S². The Hopf S³ can be taken as a rgb-graviton projection of the first SI S³ factor. The second S5 factor is used for a fiber bundle with fiber S1 to obtain a complex 2-dimensional space CP² dor the nucleon and atomic kernels geometry. It has its own inner spacetime like a bubble in its environmental spacetime and a boundary S² for the projective hedgehog caps where it exchanges energy with the environment.

The rgb-graviton whirl uses the first three λ1,2,3 matrices. For the basic spin length, it was assumed that it acts as Gleason frame for projection maps. The degenerate, numerical D3 orbit ½, 1, 2 is used as in Figure 5 where the scaled spin vector length towards the floors plane containing its upper boundary whirl is measured for fermionic particles as ½, for bosons with length 1 and rgbgravitons with 2. For generating the general relativistic rescaling rescaling of Minkowski metric two steps are necessary. First the distance between two systems P, Q in gravitational interaction having a common barycenter B is measured unsymmetrically. This was described above. Here is added that the Schwarzschild scaling factor cos²β = (r-Rs)/r is used by the rgb-graviton in nucleons for rescaling the distance between rb- or gb-diquarks exchanging a gluon. Like a spring the metrical distance as difference Δr (or differential dr) is rescaled as in the Minkowski watch (Figure 2) where the two quarks are in motion as in the SI rotor, rotating on a whirls circle, and the length Δr is measured by the rgb-graviton as Gleason frame and real cross product as area of Δr/cos β and time is squeezed as dt‘=dt∙cos β. The spiralic orthogonal projection occurs also when two galaxies get a common barycenter, start rotating about one another and the distance between them is in this case contracted until they collide. There is a toy on the market where after starting a rotation of two balls attached on a stick, they come fast close to one another until they touch. The metrical stretching of Δr occurs as second cosmic speed of Q as v²2 c²=Rs/r = sin²β when an orbital speed v of P is compared with v2 in v<v2 for rotation or v≥v2 when the common barycenter and gravitational interaction between Q,P ends and P can escape. Its lower bound for an orbit is v1=v2/√2 where for v<v1 free fall towards a barycenter occurs as rgb-graviton contraction of the distance |BP| Figure 7 first lower projection, due to the Pythagoras theorem. At the beginning of the article the radius inversion of quarks at the decaying black holes Schwarzschild radius Rs was mentioned. This scalar is used for the cosmic speeds not only for radius inverted quarks but also for large mass systems. It is set as a natural constant. The Einstein energymomentum tensor is a general relativistic computation for it and the Schwarzschil metric. Here, the setting is for a quantum gravity on nucleon base. Also, Minkowski metric has its deuteron atomic kernel base with the generation of a common group speed of its parts by rescaling mass.

1. Kalmbach GHE, Eberspaecher U (2019) Mint-wigris tool bag with handbook. Bad Woerishofen, Germany.
2. Kalmbach GHE (2017) Mint-wigris. SF J Nuclear Science, Germany.