Establishing the Constitutive Equations during Hot Tensile Deformation in an Mg-Zn-Y-Ca-Zr Alloy Fabricated by Multidirectional Forging and Rolling

Because of high modulus-to-density ratio, good specific strength, and damping performance, Mg-Zn-Y magnesium alloys have the potential for application in automobile manufacture, aerospace industry, and so forth [1-4]. Hence, a new Mg-3Zn-1Y-0.5Ca-0.5Zr (hereinafter denoted as ZWCK3100) alloy is designed. Owing to limited slip systems of magnesium at room temperature, von Mises deformation compatibility of five independent slip systems cannot be met in magnesium alloy. Thus, plastic forming of magnesium alloy such as Mg-Zn-Y magnesium alloys with a high Zn and Y content is difficult at room temperature. However, hot deformation like hot compression and hot tension can initiate the non-basal etc. slip systems and improve the plasticity of magnesium alloys like Mg-Zn-Y alloys at elevated temperature [5-9]. Thus, it is necessary to investigate the hot tensile deformation behavior of ZWCK3100 alloy. Multidirectional Forging (MDF), as a severe plastic deformation method and because of its suitable large-scale billet fabrication, has been investigated in magnesium alloys [10-14] except Mg-Zn-Y alloys, but little report is available reporting MDF of Mg-Zn-Y alloy. Meanwhile, conventional rolling has the advantage of mass production due to its high rolling speed. As per our literature survey, little work is available about combination of MDF and hot rolling to produce ZWCK3100 alloy. Thus, it is necessary to fabricate ZWCK3100 alloy plate and investigate its high temperature deformation behavior.

Constitutive modeling is an interesting topic during hot deformation, and is a prerequisite for the implementation of numerical simulation and calculation of deformation load. Constitutive modeling can be classified as phenomenological equation, physics-based constitutive equation, and Artificial Neural Network (ANN) model [15]. Due to their higher correlation coefficients and lower absolute relative errors, the phenomenological equations such as Arrhenius constitutive equation [5,6], modified Johnson-Cook constitutive equation [16], and modified Zerilli-Armstrong constitutive equation [17] in magnesium alloys were established. According to our survey, little work is reported on modeling an Arrhenius constitutive equation and a modified Fields-Backofen constitutive equation in ZWCK3100 magnesium alloy. To the best of authors’ knowledge, there is no report studying the Arrhenius constitutive equation and modified Fields-Backofen constitutive equation in the present alloy. Thus, it is necessary to establish both equations. In the present work, our research aims include three aspects:
(i) To fabricate a new ZWCK3100 alloy using MDF and hot rolling
(ii) To obtain the flow stress curves at elevated temperatures
(iii) To construct an Arrhenius constitutive equation and a modified Fields-Backofen constitutive equation in this alloy.

Pure Zn, pure Mg raw materials, Mg-30Y, Mg-30Ca, and Mg- 30Zr mater alloys were melted at 993K in an electric resistance furnace with the protection of RJ-5 flux and argon atmosphere. The analyzed alloy composition was Mg-2.70Zn-1.34Y-0.37Ca-0.02Zr (mass.%). After the melt was stirred and held for 5min, the melt was solidified into an ingot in an internally water-cooled copper crucible. After being homogenized at 673K for 14h, the ingot surface was milled to remove the cast defects. Then the milled ingot was machined by spark discharge processing into cuboid billets. The dimension of the cuboid billet was 40mm×30mm×20mm. Then MDF and rolling started. The schematic diagram of MDF and rolling was shown elsewhere [18]. The forging temperature was 673K, and the holding time during intermediate forging was 30min. The pass strain was 0.288. Then, after heated at 673K for 1h, the billet was hot rolled at 673K from 20mm thickness to 16.73mm thickness for four passes. The pass reductions were 8%, 7%, 6%, and 5.5%, respectively. The samples for tensile testing were machined along the rolling direction from above-mentioned billets and plates. The dimension of the sample for high temperature tensile test was 6mm×3mm×2mm. After annealed at 673K for 60min and held at designated testing temperatures for 15min, the tensile tests were performed on a Shimidazu- AG-Xplus 100kN tester in the temperature range of 573~723K and strain rate range of 1.67×10- 2~1.67×10^-4s^-1.

Flow stress curves at elevated temperatures

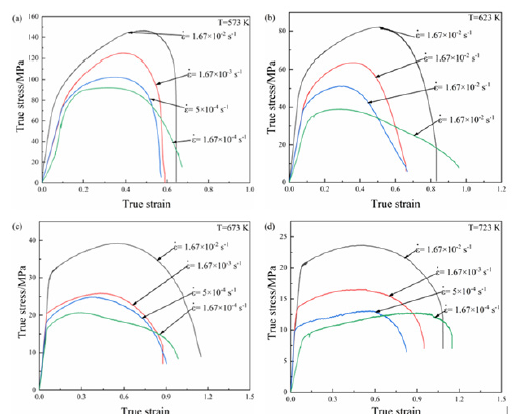
(Figure 1) presents the flow stress curves of ZWCK3100 alloy at different temperatures and initial strain rates. The flow stress curves at 723K and lower strain rates exhibit a slow strain hardening stage, followed by a strain softening stage, which indicates the occurrence of dynamic grain growth. Except for this, other flow stress curves behaves like conventional single peak curves, indicating the occurrence of dynamic recrystallization.

Figure 1:Flow stress curves of ZWCK3100 alloy at different temperatures and initial strain rates: a) 573K b) 623K c) 673K d) 723K.

Hyperbolic sine Arrhenius equation

The σ−ε relationship in the Arrhenius equation is expressed a

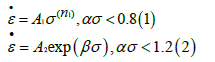
where σ−ε means the stress-strain rate, and A₁,n₁,A₂ and β are material constants.

Arrhenius equation can be expressed as [19]

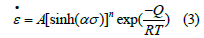
where A is the material constant, and α is the stress amplifier factor, n is the stress exponent, Q is the activation energy for deformation, J/mol, R is the universal gas constant, 8.314 J·K^-1·mol-¹ and T is the absolute temperature, K, here α=β⁄n¹.

Zener–Holloman parameter is given by [20]

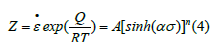
Logarithm is taken on equations (1),(2), and (3), one obtains.

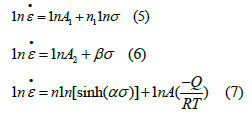
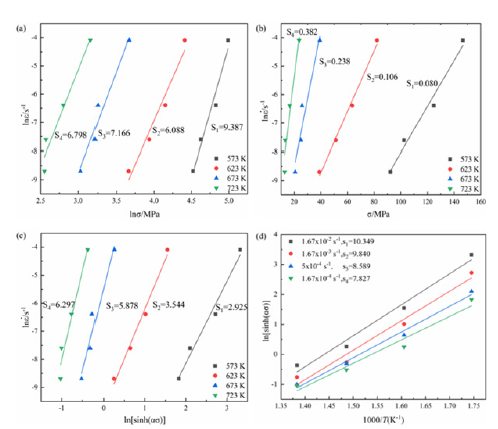
It follows from equations (5)-(7) that n₁ is the slope of 1n ε•-1nβ curve, β is the slope of 1nε σ•− curve, and n is the slope of 1nε•=1n[sinh(ασ )] as shown in (Figure 2). (Figures 2a-2d) presents the linear fit diagram of 1nσ−1nε ,σ−1nε•,1 [sinh(ασ)]−1nε• and1n[sinh(ασ )]−1000 / T , respectively. The slope of each strain line represents different material constant values. As shown in (Figure 2a), n1 values are 6.088, 6.798, 7.166, and 9.387, respectively. As shown in (Figure 2b), β values are 0.080, 0.106, 0.238, and 0.382, respectively.

Figure 2:Relational curves under different deformation conditions a) lnσ-lnε• b) σ-lnε• c) ln [sinh (ασ)]-in ε•d) ln[sinh(ασ )]−1000 / T Si(i=1,2,3,4) denotes the slope

Hence, average n1 is obtained. n1 =7.360. Average β is obtained, β=0.2015. Thus, α=β/n1=0.027. (Table 1) shows the peak stresses (MPa) of ZWCK3100 alloy under different deformation conditions. Q formula is expressed as

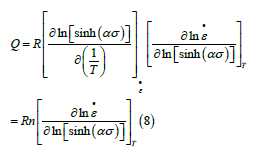
Table 1: The peak stresses (MPa) of ZWCK3100 alloy under different deformation conditions.

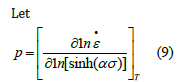
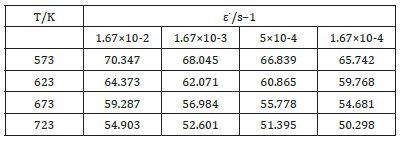
(Figure 2d) is the linear fitting of ln sinh (ασ ) −1000 / T . Its slope is p. Hence, as per equations (8) and (9), one gets Q = R× n× p. Thus, Q values under different conditions can be obtained, as shown in (Table 2). The average activation energy for deformation is 354.625kJ/mol. Substitution of Q values and other relevant parameters into equation (4), lnZ is obtained (Table 3) shows the lnZ values of ZWCK3100 alloy under different deformation conditions.

Figure 3:Fitting line of ZWCK3100 alloy a)lnZ- ln[sinh(ασ)] b)Comparison of predicted stress and experimental stress

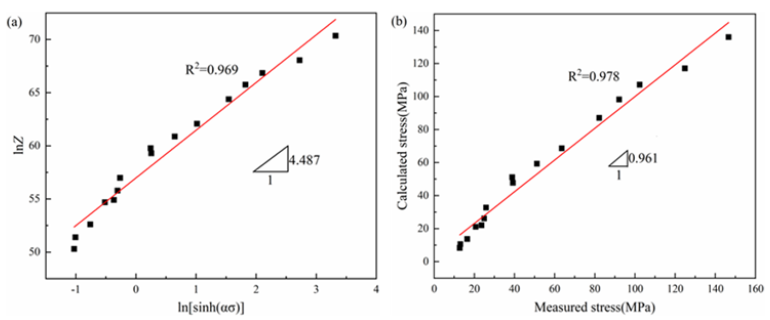
Table 2: Deformation activation energy of ZWCK3100 alloy under different deformation conditions: kJ/mol.

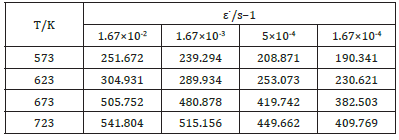
Table 3: lnZ values of ZWCK3100 alloy under different deformation conditions.

(Figure 3a) shows the linear fit curve of ln Z − ln sinh (ασ ) . The slope is stress exponent n, and the intercept is lnA. Hence, n=4.487. lnA=56.975, hence A=5.545×10²⁴. (Figure 3b) presents the comparison of predicted stress and experimental stress. The determination coefficient, R², is 0.978, and the slope is 0.961, very close to 1, which indicates that such a model is excellent.

Above-mentioned data is substituted into equation (3) gives

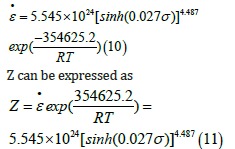
As per equations (10) and (11), the flow stress in Arrhenius equation can be obtained.

(Figure 3b) presents the comparison result of predicted stress and experimental stress. The determination coefficient was 0.978, the ratio of prediction stress to experimental stress was 0.961, indicative of excellent agreement. To validate the accuracy of Arrhenius equation, Average Absolute Relative Error (AARE) is used to characterize the prediction capability of the model:

where N-number of stress value,E_i − experimental stress, and P_i− predicted stress. Thus, AARE=2.1%, indicative of excellent fitting effect.

Figure 4:The relation curves between different parameters a)n-value under different conditions b)fitting curve between predicted n-value and experimental n-value c)m-value under different conditions d)relation curve of lnσ-T.

Modified Fields-Backofen constitutive equation

Fields-Backofen constitutive equation is given by the following [21]

where K—hardening coefficient; n—strain-hardening exponent; m—strain ratesensitivity index. Fields-Backofen equation describes well the strain-hardening process, but in consideration of the softening stage in the flow stress curves, a modified Fields-Backofen equation considering the softening stage is required and given by [22]

where b —softening ratio; s —softening parameter. Logarithm is taken on equation (15), one obtains the following:

Relevant parameters can be obtained according to the relationship between 1nσ , 1nε , 1n ε • and T.

Strain-hardening exponent n-value: As shown in (Table 4), n-values can be obtained as per the relationship between 1nσ and 1nε , n-values are fitted with 1/T and 1n ε • , one gets formula (17)

The experimental parameters are substituted into above formula, the predicted n-values are shown in (Table 5). The fitting effect is shown in (Figures 4a & 4b). The determination coefficient is 0.832, and the slope is 0.868, indicative of good fitting.

Table 4: The n-values of ZWCK3100 alloy under different deformation conditions

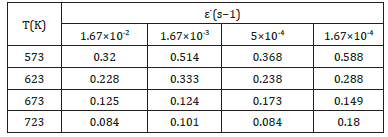
Table 5: The predicted n-values of ZWCK3100 alloy under different deformation conditions.

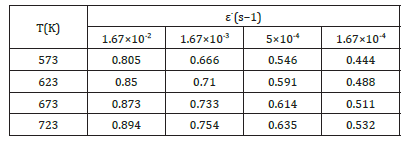
Figure 5:The relation curves between different parameters a)n-value under different conditions b)fitting curve between predicted n-value and experimental n-value c)m-value under different conditions d)relation curve of lnσ-T.

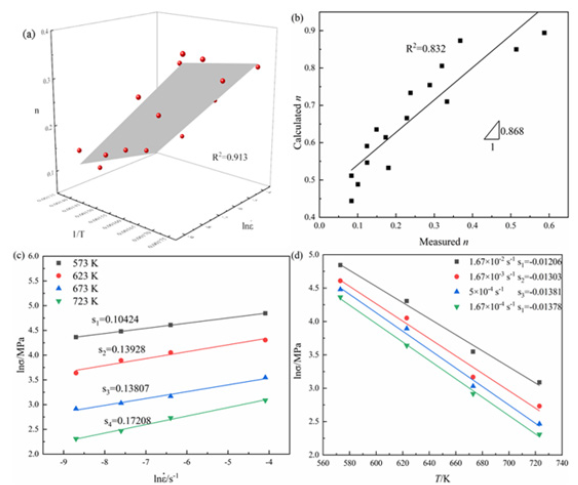
Strain rate sensitivity index-m-value: As per (Figure 4c), the fitted formula of m-values at different temperatures is shown in equation (18):

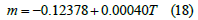
Softening ratio b: As is shown in (Figure 4d), at four experimental strain rates, the softening ratios of this alloy are -0.01206, -0.01303, -0.01381 and -0.01378, respectively. The mean value is b-value, b=-0.01317.

Softening parameter s: Presuming that 1nK+m1nε+bT is K₁ at given temperature and strain rate, when ε=e^-1.5 and ε=e^-2, equation (15) is simplified as:

After equation (19) subtracts equation (20), one obtains

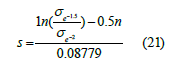
Substitution of experimental data into above equation, s values under different conditions are obtained. s values are fitted with 1/T and 1n ε • , one gets (Figure 5a). The determination coefficient of comparing predicted value and experimental values is 0.950 with good fitting effect. Hence, equation (22) is obtained:

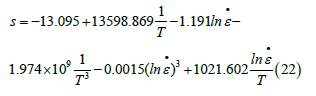
Figure 6:The relation curves between different parameters a)s as a function of 1/T and ln ε • b)K as a function of 1/T and ln ε

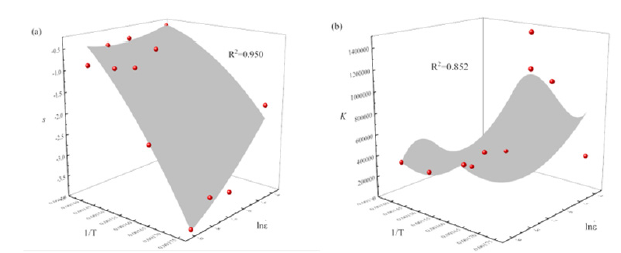
Hardening parameter K: As shown in (Figure 5b), the relation curves of K as a function of 1/T and ln ε • . The determination coefficient is 0.852 with good fitting effect. Thus, equation (23) is obtained

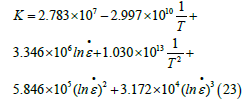
Aforementioned parameters are substituted into equation (15), a modified Fields-Backofen constitutive equation was established as follows:

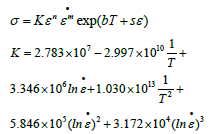
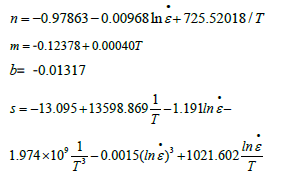
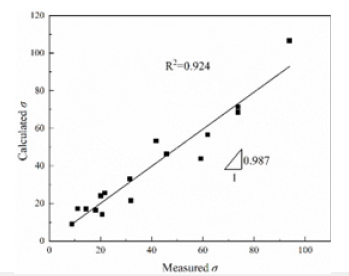
Validation of predicted stress and experimental stress using established Fields-Backofen equation: Substitution of experimental parameters into above-mentioned formula, the predicted stresses can be obtained. (Figure 6) presents the validation curve between predicted stresses and experimental stresses. The determination coefficient is 0.924, and the fitting slope is 0.987, which indicate that the predicted flow stress is slightly lower than the experimental stress.

Figure 7:Validation curve between predicted stress and experimental stress

(i) The flow stress curves at 723K and lower strain rates exhibit a slow strain hardening stage, followed by a strain softening stage. Except for this, other flow stress curves behave like conventional single peak curves.
(ii) An Arrhenius constitutive equation was established:

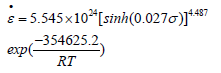
The determination coefficient was 0.978, the ratio of predicted stress to experimental stress was 0.961, and the average absolute relative error was 2.1%, implying high accuracy of the hyperbolic sine law.
(iii) A modified Fields-Backofen constitutive equation was established:

The determination coefficient was 0.924, and the ratio of prediction stress to experimental stress was 0.987, indicative of high precision.

1. Dai S, Wang F, Wang Z, Liu Z, Mao PL (2020) Microstructure, mechanical properties, and texture evolution of Mg-Zn-Y-Zr alloy fabricated by hot extrusion-shearing process. J Mater Sci 55: 375-388.
2. Hao JQ, Zhang JS, Li BQ, Xie RZ (2021) Effects of 14H LPSO phase on the dynamic recrystallization and work hardening behaviors of an extruded Mg-Zn-Y-Mn alloy. Mater Sci Eng A 804: 140727.
3. Bazhenov VE, Saidov SS, Tselovalink Yu V, Voropaeva OO, Plisetskaya IV, et al. (2021) Comparison of castability, mechanical, and corrosion properties of Mg-Zn-Y-Zr alloys containing LPSO and W phases. Trans Nonferrous Met Soc China 31:1276-1290.
4. Dong XR, Yu H, Kang SM, Yu W, Jiang BA, et al. (2021) A comparable study of Mg₁₅Y₁Zn_0.85 sheets fabricated by twin-roll casting and direct-chill casting and related annealing behavior. Mater Sci Eng A 815:141316.
5. Kwak TY, Lim HK, Kim WJ (2017) Effect of the volume fraction of the icosahedral phase on the microstructures, hot compressive behaviors and processing maps of Mg-Zn-Y alloys. J Alloys Compd 725: 711-723.
6. Gao FY, Yang LW, Fan ZB, Lin XP, Yang YS, et al. (2022) Effects of morphology and I-Mg₃Zn₆Y second-phase distribution on hot-compressive-deformation behavior of Mg-Zn-Y-Zr alloy under a strain rate of 1.0s^-1. Mater Sci Eng A 834: 142556.
7. Hao JQ, Zhang JS, Gong XY, Li BQ (2021) Hot deformation behavior and workfability of the homogenized Mg-5.8Zn-1.2Y-1Mn alloy containing I and W phases. J Mater Res Technol 15: 2202-2212.
8. Li LH, Qi FG, Wang Q, Hou CH, Zhao N, et al. (2020) Hot deformation behavior of Mg₂₁Zn_1.44Y_2.86Mn_0.49 alloy containing LPSO phase. Mater Charact 169: 110649.
9. Fata A, Faraji G, Mashhadi MM, Tavakkoli V (2016) Hot tensile deformation and fracture behavior of ultrafine-grained AZ31 magnesium alloy processed by severe plastic deformation. Mater Sci Eng A 674: 9-17.
10. Mehrabi A, Mahmudi R, Miura H (2019) Superplasticity in a multi-directionally forged Mg-Li-Zn alloy. Mater Sci Eng A 765:138274.
11. Azizi A, Mahmudi R (2019) Superplasticity of fine-grained Mg-xGd alloys processed by multi-directional forging. Mater Sci Eng A 767: 138436.
12. Li JL, Wu D, Yang QB, Chen RS (2016) Superplasticity of multi-directional impact forged Mg-Gd-Y-Zr alloy. J Alloys Compd 672: 27-35.
13. Kandalam S, Sabat RK, Bibhanshu N, Avadhani GS, Kumar S, et al. (2017) Superplasticity in high temperature magnesium alloy WE43. Mater Sci Eng A 687: 85-92.
14. Miura H, Minami K, Kobayashi M, Watanabe C (2021) Multi-directional forging and warm extrusion of AZ80Mg Alloys. Mater Trans 62: 610-619.
15. Lin YC, Chen XM (2011) A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater Des 32: 1733-1759.
16. Cao FR, Sun CF, Liu SY, Liang JR, Liu RJ, et al. (2022) Microstructures, hot tensile deformation behavior and constitutive modeling in a superlight Mg-2.76Li-3Al-2.6Zn-0.39Y alloy. J Alloys Compd 896: 163049.
17. Cao FR, Guo HZ, Guo NP, Kong ST, Liang JR (2023) Room-temperature strengthening, portevin-le chatelier effect, high-temperature tensile deformation behavior, and constitutive modeling in a lightweight Mg-Gd-Al-Zn Alloy. Mater 16(4): 1639.
18. Cao FR, Zhang J, Ding X, Xue GQ, Liu SY, et al. (2019) Mechanical properties and microstructural evolution in a superlight Mg-6.4Li-3.6Zn-0.37Al-0.36Y alloy processed by multidirectional forging and rolling. Mater Sci Eng A 760: 377-393.
19. Mirzadeh H (2019) Developing constitutive equations of flow stress for hot deformation of AZ31 magnesium alloy under compression, torsion, and tension. Int J Mater Form 12:643-648.
20. Zener C, Hollomon JH (1944) Effect of strain rate upon plastic flow of steel. J Appl Phys 15: 22-32.
21. Fields DS, Backofen WA (1957) Determination of Strain Hardening Characteristics by Torsion Testing. Proc ASTM 57: 1259-1272.
22. Ji GL, Li L, Qin FL, Zhu LY, Li Q (2017) Comparative study of phenomenological constitutive equations for an as-rolled M50NiL steel during hot deformation. J Alloys Compd 695: 2389-2399.