- Submissions

Full Text
COJ Technical & Scientific Research
Is a Soliton Possible in In-Situ Combustion?
Pablo C*
Department of Mathematics, Autonomous Technological Institute of Mexico (ITAM), Mexico
*Corresponding author: Pablo Castañeda, Department of Mathematics, Autonomous Technological Institute of Mexico (ITAM), RIO Hondo 1, Ciudad De Mexico 01080, Mexico
Submission: October 05, 2021; Published: October 26, 2021

Volume3 Issue4October, 2021
Opinion
Is ignition or extinction the fate of an in-situ combustion that occurs in a bounded region within an oil reservoir? It is well known that such combustion helps with the extraction of heavy oils. The process burns small amounts of crude oil and increasing recovery by lowering the density of the oil downstream. However, how to maintain such behavior within the reservoir is not fully understood. To overcome this problem, an unconventional approach comes from a simple reaction model that “moves” at constant speed, set by reservoir and injection temperatures. Reaction speed and temperature are found for any configuration; the proposed model can have more than one solution profile, a stability analysis of which reveals the behavior of those solutions. A practical conclusion is the challenge of maintaining the conditions for such profiles to exist with a rich combustion that is maintained for waves that expand in two or three dimensions. Maintaining the initial combustion behavior requires oxygen injection to increase over time [1]. Although there is a vast engineering literature on chemical reactors in porous media, we have no knowledge of mathematical studies on asymptotic behavior of such reactors, i.e., the maintenance of combustion or extinction. The seminal study is based on a static reaction, (2), in (1) we study the dynamics of said reaction. There may be three equilibria related to combustion, oxidation and a third non-physical state separating the basins of attraction of the other two. This note is based on the previous studies, we may look “by hand” for traveling waves in a thin reservoir tube. The assumption that the wave burns all the available fuel in its trail is an efficient condition for in-situ combustion. Considering homogeneous temperature in the reaction, the heat conduction occurs in the reservoir direction. For given injection and reservoir temperatures, wave speeds and reaction temperatures for stable solitons are found.
For a thin porous media tube a toy model can be derived from first principles. The profiles are governed by the adimensionalized model

for the adimensionalized temperature u given as the ratio of the temperature in kelvin
degrees times the universal constant of ideal gases divided by the activation energy of the
Arrhenius reaction, as TR/E, the Damkohler group IV number  relates the “released
heat” with the “conductive heat loss”, and
relates the “released
heat” with the “conductive heat loss”, and 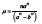 is capable of set the equations for
Rn with
radial symmetry, see [1, App.A]. Here, the geometrical parameters may be taken a=2 and
b=0. The main issue is to establish the speed σ and
is capable of set the equations for
Rn with
radial symmetry, see [1, App.A]. Here, the geometrical parameters may be taken a=2 and
b=0. The main issue is to establish the speed σ and 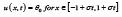 as the reaction
temperature. A Cole-Hopf transform ξ = x −σ t shows that both solutions must satisfy the
Wentzell boundary conditions
as the reaction
temperature. A Cole-Hopf transform ξ = x −σ t shows that both solutions must satisfy the
Wentzell boundary conditions
(1b) and (2b) surrounding the reaction as
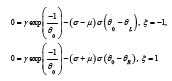
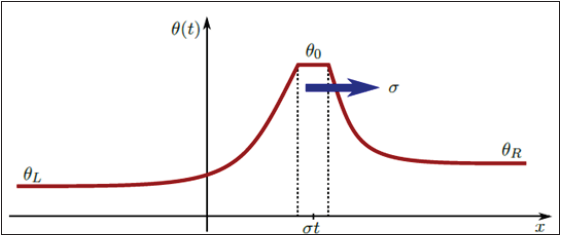
equating the reservoir θ R and injected L θ temperatures, show a traveling wave profile as the sketch in (Figure 1). These equations also leads to left and right conditions, to be satisfied,
Figure 1: Typical soliton profile; reservoir temperature larger than injected temperature . Here is reaction temperature and σ the front speed of the traveling wave.
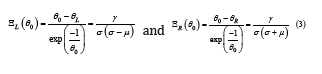
It is expected 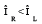 which is satisfied for σ > μ . For inputs θL < θR the desirable outputs are realistic 0θ and σ . From relations (3) we get the front speeds
which is satisfied for σ > μ . For inputs θL < θR the desirable outputs are realistic 0θ and σ . From relations (3) we get the front speeds
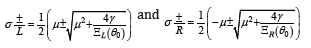
So positive and equal speeds to form a traveling wave front (with 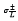 and
and 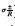 are found with the auxiliary functions
are found with the auxiliary functions 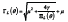 and
and 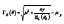 the intersections of which are of special interest.
the intersections of which are of special interest.
The ordered pair θL <θR grants a solution. Are there more? It can be, for example, let θ L = 0.016
(about 300oK) and θ R = 0.025 (about 475oK), we have two solutions:
i. The computed speed σ ≈ 0.6953 is equivalent to 6.953 10 2mm / s × − ; less than 5mm per minute. However, the computed adimensionalized temperature θ0 = 0.04949 is a good estimate for combustion, about 927.23o K.
ii. The computed speed is equivalent to a reasonable 0.53m/s. In this scenario there is a “really high” temperature of 447; 871.87o K exceeding by two orders of magnitude the Sun’s average temperature.
The second solution is unstable and the dynamics will approach to the stable one, calibrating the parameters could show more realistic values even in this toy model. This is a hard issue since combustion occurs in only 20cm for large reservoirs; moreover, in this model changing the combustion area has a quadratic response for the soliton speed. In one hand the complete stability analysis is missing, on the other, defining the number of solutions is not an easy task; there may be three solutions. It is important to understand the behavior of the auxiliary functions ΓL (θ) and ΓR (θ) for any initial data θ L ,θ R , the search for the number of possible solutions and bifurcations, and so determine their stability for more general cases. The one-dimensional analysis can be replicated in larger dimensions generating realism in the field. However, considering radial solutions in more dimensions, a promote result is that the soliton at constant speed would increase the area or volume of combustion as the front advances, so it needs a greater amount of oxygen to maintain such combustion. A more delicate issue is that for this scenario, the front would also have higher speeds in its advance [2].
This cannot be maintained as recorded in the field. On the other hand, combustion for this toy model needs the so-called “cracking” downstream, generating coke at the same rate at which combustion develops, so the balance between speed and burning remains a delicate issue. In any case, to maintain an in-situ combustion, it will be necessary to inject an increasing amount of oxygen, being limited by the dimensions of the reservoir, hindering therefore the existence of the radial soliton in in-situ combustion. The hope of achieving a combustion wave is then restricted to fronts that piston-like movement. Fingering and sweeping of the fronts have to be carefully calculated.
References
- Castaneda P, Marchesin D, Bruining J (2012) The dynamics of chemical reactors in porous media. Advanced Differential Equations 17(7): 725-746.
- Tadema HJ, Weijdema J (1970) Spontaneous ignition of oil sands. Oil Gas J 68: 77-80.
© 2021 Pablo Castañeda. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






