Drag Force Analysis for an Inertial Microfluidics Device

Microelectromechanical and nanoelectromechanical systems (MEMS and NEMS) made of ultra-small structures have shown many fascinating functions and abilities in recent years [1- 8]. More specifically, new promising techniques have been proposed in medicine to diagnose a range of diseases based on MEMS and NEMS [9]. Compared to traditional methods, these new methods display a fast-reliable analysis. In addition, the final size of these systems is comparatively very small since the most common fundamental building blocks of these systems are microscale structures [10-22] and nanoscale structures [23-29]. Due to their small size, they can be utilized everywhere regardless of lab equipment and facilities [30]. Microfluidics-based technology has been shown to be very promising for many applications in the field of microtechnology including water purification, drug delivery, virus detection and cell separation [31]. For instance, Shafiee et al. [32] invented a microfluidics-based microscale sensor, which is able to detect human immunodeficiency virus (HIV) in blood samples. This sensor is small, light and unexpansive, which make it an ideal candidate for HIV screening in areas in which there is no access to advanced hospital equipment and trained technicians. Microfluidics-based devices are divided into different groups according to their size, applications and governing forces. One widespread categorization of these ultra-small devices is based on governing forces. According to this categorization, there are two types of microfluidics-based devices:

a. Active, and

b. Passive.

If there are external forces, which act on the particles and fluids inside the microfluidicsbased device, it belongs to the active group. By contrast, if the particles and fluids are subject to intrinsic forces such as drag, inertial and wall-induced forces, the microscale device is considered as passive. Each group of microfluidics-based devices is also divided to several sub-groups. One of significant sub-groups of passive microfluidics-based technology is inertial microfluidics, which is focused in this paper. Inertial microfluidics has shown a promising potential in various biomedical applications such as the separation of rare ultrasmall biological objects and the preparation of biological samples. In these applications, when an ultra-small object moves in a flowing fluid, various forces including Magnus, Saffman and drag forces act on the object, and significantly affect its motion. In this work, the drag force, as an important intrinsic force in a microfluidic channel, as well as the drag coefficient are analytically examined. Explicit expressions are given for this important force. Moreover, the influences of particle diameter on the drag force and coefficient are analyzed.

Figure 1:Schematic representation of drag force due to the mainstream flow in an inertial microfluidic channel.

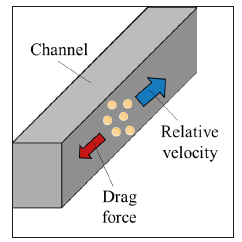
When an ultra-small object travels in an inertial microfluidic channel, due to the need for carrying away other ultra-small objects such as fluid molecules, a load, which is called drag force, is exerted on the ultra-small object (Figure 1). Assuming that this object has a spherical shape. In addition, the deformation of the ultra-small object itself is neglected. The relative velocity between the object and fluid is indicated by Ur. The drag force is obtained as [33]

in which c_drag, A_obj, and d_obj are, respectively, drag coefficient, the area of the object cross-section and object diameter. The drag coefficient and consequently the drag force are a function of object Reynolds number Re_obj that is given as

In Eq. (2), and as well as Ur indicate the fluid viscosity and density as well as relative speed, respectively. It is worth stating that size effects are ignored in these relations. Size effects are commonly incorporated for analyzing the dynamics of nonstructural components [29,34-36]. It is assumed that 0.2< ReP< 500 1000. For this range of Reynolds number, the drag coefficient and force are [33,37]

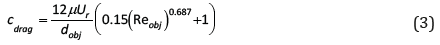
and

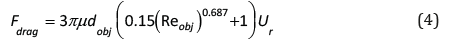
More information and assumptions about the derivation procedure of Eqs. (3) and (4) are given in Refs. [33,37]. In inertial microfluidics, the drag force is generated in two main cases:

A. In the mainstream, and

B. In the secondary flow.

The first one exists along the axial axis of the microfluidic channel whereas the second one is in the cross-section of the microfluidic channel. Equations (3) and (4) are valid for the mainstream flow in inertial microfluidics provided that the object Reynolds number does not exceed the above-mentioned range. Inertial microfluidic systems usually work in an intermediate Reynolds number, which belongs to a smaller range inside the above-mentioned range. From Eq. (3), it can be concluded that if the diameter of the ultrasmall object increases, the drag coefficient decreases. Nonetheless, the object diameter has an increasing effect on the drag force, as seen from Eq. (4). In addition, other parameters such as fluid viscosity, the relative velocity of particles with respect to fluid and Reynolds number have important effects on the drag force inside an inertial microfluidics-based device. For instance, if the relative velocity diminishes, the drag coefficient decreases due to two main reasons. First of all, as can be concluded from Eq. (3), the reduction in relative velocity directly results in lower drag forces. Secondly, when particles travel with a lower relative velocity, Reynolds number decreases according to Eq. (2), and this leads to a reduction in the drag force as well. In a similar way, when the relative velocity is reduced, the drag force is also noticeably reduced, as can be seen from Eq. (4). This analysis and formulation would help researchers with the analysis of small-scale systems used to convey fluid [38- 44] and a mixture of particles and fluid [37,45,46].

The drag force and coefficient have been analyzed in inertial microfluidic channels. Analytical expressions were given for both drag force and coefficient in an appropriate range of object Reynolds numbers for spherical rigid ultra-small objects. It was found that the drag coefficient, which affects the motion of ultrasmall objects in a microfluidic channel, decreases with increasing the object diameter whereas the drag force substantially increases when the diameter of the object grows.

1. Şimşek M (2016) Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach. International Journal of Engineering Science 105: 12-27.
2. Farokhi H, Ghayesh MH (2018) Nonlinear mechanics of electrically actuated microplates. International Journal of Engineering Science 123: 197-213.
3. Ghayesh MH (2018) Mechanics of tapered AFG shear-deformable microbeams. Microsystem Technologies 24(4): 1743-1754.
4. Ghayesh MH (2018) Functionally graded microbeams: Simultaneous presence of imperfection and viscoelasticity. International Journal of Mechanical Sciences 140: 339-350.
5. Ghayesh MH, Farokhi H, Amabili M (2013) Nonlinear behaviour of electrically actuated MEMS resonators. International Journal of Engineering Science 71: 137-155.
6. Ghayesh MH, Farokhi H, Alici G (2015) Size-dependent electro-elastomechanics of MEMS with initially curved deformable electrodes. International Journal of Mechanical Sciences 103: 247-264.
7. Farokhi H, Ghayesh MH (2017) Nonlinear thermo-mechanical behaviour of MEMS resonators. Microsystem Technologies 23(12): 5303-5315
8. Farokhi H, Ghayesh MH (2016) Size-dependent behaviour of electrically actuated microcantilever-based MEMS. International Journal of Mechanics and Materials in Design 12(3): 301-315.
9. Shafiee H, Wang S, Inci F, Toy M, Henrich TJ, et al. (2015) Emerging technologies for point-of-care management of HIV infection. Annu Rev Med 66: 387-405.
10. Farokhi H, Ghayesh MH (2017) Nonlinear resonant response of imperfect extensible timoshenko microbeams. International Journal of Mechanics and Materials in Design 13(1): 43-55.
11. Ghayesh MH, Farokhi H (2017) Parametric vibrations of imperfect timoshenko microbeams. Microsystem Technologies 23: 4917-4929.
12. Farokhi H, Ghayesh MH, Hussain S (2016) Dynamic stability in parametric resonance of axially excited timoshenko microbeams. Meccanica 51(10): 2459-2472.
13. Farokhi H, Ghayesh MH, Kosasih B, Akaber P (2016) On the nonlinear resonant dynamics of timoshenko microbeams: effects of axial load and geometric imperfection. Meccanica 51(1): 155-169.
14. Ghayesh MH (2019) Viscoelastic dynamics of axially FG microbeams. International Journal of Engineering Science 135: 75-85.
15. Ghayesh MH (2019) Viscoelastically coupled dynamics of FG timoshenko microbeams. Microsystem Technologies 25(2): 651-663.
16. Ghayesh MH, Farajpour A (2018) Vibrations of shear deformable FG viscoelastic microbeams. Microsystem Technologies 25(4): 1387-1400.
17. Ghayesh MH, Farajpour A (2019) A review on the mechanics of functionally graded nanoscale and microscale structures. International Journal of Engineering Science 137: 8-36.
18. Ghayesh MH, Farokhi H (2016) Coupled nonlinear dynamics of geometrically imperfect shear deformable extensible microbeams. Journal of Computational and Nonlinear Dynamics 11(4): 10.
19. Ghayesh MH, Farokhi H, Hussain S (2016) Viscoelastically coupled size-dependent dynamics of microbeams. International Journal of Engineering Science 109: 243-255.
20. Ghayesh MH, Farokhi H (2017) Bistable nonlinear response of MEMS resonators. Nonlinear Dynamics 90: 1627-1645.
21. Farokhi H, Ghayesh MH (2018) Supercritical nonlinear parametric dynamics of timoshenko microbeams. Communications in Nonlinear Science and Numerical Simulation 59: 592-605.
22. Rashvand K, Rezazadeh G, Mobki H, Ghayesh MH (2013) On the sizedependent behavior of a capacitive circular micro-plate considering the variable length-scale parameter. International Journal of Mechanical Sciences 77: 333-342.
23. Farajpour A, Ghayesh MH, Farokhi H (2018) A review on the mechanics of nanostructures. International Journal of Engineering Science 133: 231-263.
24. Ghayesh MH, Farajpour A (2018) Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. International Journal of Engineering Science 129: 84-95.
25. Farajpour A, Rastgoo A, Farajpour M (2017) Nonlinear buckling analysis of magneto-electro-elastic CNT-MT hybrid nanoshells based on the nonlocal continuum mechanics. Composite Structures 180: 179-191.
26. Farajpour A, Ghayesh MH, Farokhi H (2019) Large-amplitude coupled scale-dependent behaviour of geometrically imperfect NSGT nanotubes. International Journal of Mechanical Sciences 150: 510-525.
27. Farajpour M, Shahidi A, Tabatabai-Nasab F, Farajpour A (2018) Vibration of initially stressed carbon nanotubes under magneto-thermal environment for nanoparticle delivery via higher-order nonlocal strain gradient theory. The European Physical Journal Plus 133: 219.
28. Farajpour M, Shahidi A, Farajpour A (2018) A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Materials Research Express 5: 035026.
29. Asemi SR, Farajpour A (2014) Vibration characteristics of doublepiezoelectric- nanoplate-systems. Micro & Nano Letters 9(4): 280-285.
30. Warkiani ME, Khoo BL, Wu L, Tay AKP, Bhagat AAS, et al. (2016) Ultrafast, label-free isolation of circulating tumor cells from blood using spiral microfluidics. Nat Protoc 11(1): 134-148.
31. Bhagat AAS, Bow H, Hou HW, Tan SJ, Han J, et al. (2010) Microfluidics for cell separation. Med Biol Eng Compu 48: 999-1014.
32. Shafiee H, Jahangir M, Inci F, Wang S, Willenbrecht RB, et al. (2013) Acute on‐chip HIV detection through label‐free electrical sensing of viral nanolysate. Small 9(15): 2553-2563.
33. Coulson JM, Richardson JF, Backhurst JR, Harker JH (1991) Particle technology and separation processes. Pergamon Press, United Kingdom.
34. Asemi SR, Farajpour A, Borghei M, Hassani AH (2014) Thermal effects on the stability of circular graphene sheets via nonlocal continuum mechanics. Latin American Journal of Solids and Structures 11(4): 704- 724.
35. Farajpour A, Rastgoo A (2017) Influence of carbon nanotubes on the buckling of microtubule bundles in viscoelastic cytoplasm using nonlocal strain gradient theory. Results in physics 7: 1367-1375.
36. Farajpour A, Rastgoo A, Mohammadi M (2017) Vibration, buckling and smart control of microtubules using piezoelectric nanoshells under electric voltage in thermal environment. Physica B: Condensed Matter 509: 100-114.
37. Zhang J, Yan S, Yuan D, Alici G, Nguyen NT, et al. (2016) Fundamentals and applications of inertial microfluidics: A review. Lab on a Chip 16: 10-34.
38. Farajpour A, Ghayesh MH, Farokhi H (2019) A coupled nonlinear continuum model for bifurcation behaviour of fluid-conveying nanotubes incorporating internal energy loss. Microfluidics and Nanofluidics 23: 34.
39. Farokhi H, Ghayesh MH, Gholipour A, Hussain S (2018) Modal interactions and energy transfers in large-amplitude vibrations of functionally graded microcantilevers. Journal of Vibration and Control 24(17): 3882-3893.
40. Ghayesh MH, Farokhi H, Farajpour A (2019) Global dynamics of fluid conveying nanotubes. International Journal of Engineering Science 135: 37-57.
41. Farajpour A, Farokhi H, Ghayesh MH (2019) Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. European Journal of Mechanics-A/Solids 74: 281-296.
42. Farajpour A, Farokhi H, Ghayesh MH, Hussain S (2018) Nonlinear mechanics of nanotubes conveying fluid. International Journal of Engineering Science 133: 132-143.
43. Ghayesh MH, Farokhi H (2018) On the viscoelastic dynamics of fluidconveying microtubes. International Journal of Engineering Science 127: 186-200.
44. Farajpour A, Ghayesh MH, Farokhi H (2019) Application of nanotubes in conveying nanofluid: a bifurcation analysis with consideration of internal energy loss and geometrical imperfection. Microsystem Technologies pp. 1-15.
45. Di Carlo D (2009) Inertial microfluidics. Lab on a Chip 9(21): 3038-3046.
46. Kuntaegowdanahalli SS, Bhagat AAS, Kumar G, Papautsky I (2009) Inertial microfluidics for continuous particle separation in spiral microchannels. Lab Chip 9(20): 2973-2980.