Applications of the Intelligent Combinatorial Configurations for Advanced Mechatronic and Coding Systems

Combinatorial problems arise in many areas of pure mathamatics, notably in algebra, probability theory, topology, and geometry, and combinatorics has many applications in mathematical optimization, computer science, and statistical physics. One of the most acceptable parts of combinatorics is graph theory, which also has numerous natural connections to other areas. Combinatorial optimization started as a part of combinatorics and graph theory, but now viewed as a branch of applied mathematics and computer science, related to operation research, algorithm theory and computational complexity theory. Coding theory started as a part of design theory with combinatorial constructions of errorcorrecting codes [1]. The main idea of the subject is to design efficient and reliable methods of data transmission. It is a large field of study, part of information theory [2]. Combinatorial configurations such as cyclic difference sets [3] and Ideal Ring Bundles [4], is known, to be of very important in systems engineering for improving the quality indices of devices or systems with non-uniform structure (e.g. arrays of radar systems) with respect to resolving ability [5]. The paper regards techniques for the development of two- and multidimensional vector data coding design, based on the idea of “perfect” spatial combinatorial configurations and the generalization of these methods and results to the improvement and optimization of a larger class of technological systems, including application to coded design of signals for communications and control.

Optimum chain ordered sequences

The “ordered chain” approach to the study of elements and events is known to be of widespread applicability, and has been extremely effective when applied to the problem of finding the optimum ordered arrangement of structural elements in a distributed trechnological systems. Let us calculate all Sn sums of the terms in the numerical n-stage chain sequence of distinct positive integers Cn = {k1 , k2 ,…, kn}, where we require all terms in each sum to be consecutive elements of the sequence. Clearly the maximum such sum is the sum S_c= k₁ + k₂ +…+ k_n of all n elements; and the maximum number of distinct sums is

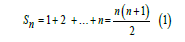
If we regard the chain sequence C_n as being cyclic, so that k_n is followed by k₁ , we call this a ring sequence. A sum of consecutive terms in the ring sequence can have any of the n terms as its starting point and can be of any length (number of terms) from 1 to n-1. In addition, there is the sum Sn of all n terms, which is the same independent of the starting point. Hence the maximum number of distinct sums S_max of consecutive terms of the ring sequence is given by

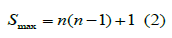
Comparing the equations (1) and (2) we see that the number of sums S_max for consecutive terms in the ring topology is nearly double the number of sums S_n in the daisy-chain topology, for the same sequence C_n of n terms.

Ideal ring bundles

An n-stage ring sequence Cⁿ={k¹,k²,...,kⁿ} of integers for which the set of all Sⁿ circular sums enumerates of natural numbers from 1 to Sⁿ-1=n(n-1) is called an “Ideal Ring Bundle” (IRB). A more general type of IRB, where the Sn ring-sums of consecutive terms give us integer value from 1 to M exactly R times, as well as the sum of all n terms exactly once. Here we see that:

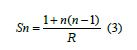
Here is an example of an IRB with n=4, R=1 and S_n = 13, namely {1, 3, 2, 7}. To see this, we observe : 1, 2, 3, 4=1+3, 5=3+2, 6= 1+3+2, 7, 8=7+1, 9=2+7, 10=2+7+1, 11=7+1+3, 12=3+2+7, 13=1+3+2+7. The Ideal Ring Bundles provide an ability to reproduce many combinatorial varieties in system with non-uniform structure due to its remarkable properties and the intelligent structure. However, it is not very simply to study and use these properties without its applicable design.

An IRB rotational Speed to Code Converter

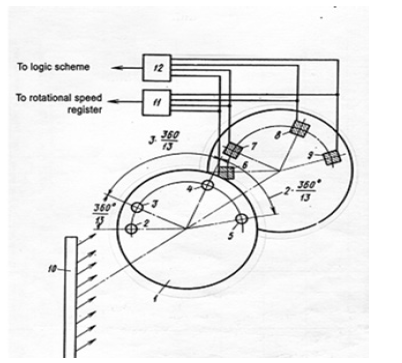
The sketch (Figure 1) shows a circuit design of rotational speed to code converter created on the IRB (1,7,2,3) code wheel [6]. Code wheel 1 has, for example, four (n=4) holes 2-5, which form n(n- 1)=12 non equal one relative to other angular shifts, sensors 6-9 fixed also with the same non equaled relative shifts, light source 10, as well as logic elements 11 AND gates, and 12 OR gates. Their inputs connected to outputs of sensors, while the outputs with register of rotational speed and logic system correspondently. Now, the output signal of AND gate will appear fixing the next rotation of wheel on 360o. In case of rotation of wheel with uneven speed, this irregularity will appear in a sequence of pulses on output elements, and the logical framework formed signals corresponding to instantaneous velocity and direction of the wheel rotation. The number of wheel holes determines the resolution of the converter. Therefore, we prefer to have higher number of holes within the code wheel for better resolution.

Figure 1: A circuit design of rotational speed to code converter constructed on the IRB (1,7,2, 3) code wheel.

Encoding design on the numerical IRBs

An n-digit IRB-code is weighed binary code, where all allowed combinations contains no more than two blocks of the eponymous symbols known as “monolithic” IRB-code. The IRB {1, 4, 6, 2} provides ring monolithic encoding design of all integers from 1 to 13 exactly once (R=1). Note, that all combinations of monolithic IRB-codes contain no more two blocks of the eponymous symbols (Table 1).

Table 1:Monolithic IRB-code (4, 6, 2, 1).

Encoding design on the two-dimensional IRBs

Let us calculate all S sums of terms in an n-stage cyclic sequence of non-negative integer 2-stage sub-sequences (2D vectors) of the sequence Cn2 = {(k₁₁, k₁₂), (k₂₁, k₂₂),…, (k_i1, k_i2),…, (k_n1, k_n2)}, where vector (kn1, kn2) is followed by (k11, k12). We require all terms in each modular 2D vector sum to be consecutive elements of the cyclic sequence, and a modulo sum m₁ of k_i2 and a modulo sum m₂ of k_i2 are taken, respectively. A modular 2D vector sum of consecutive terms in this sequence can have any of the n terms as its starting point and can be of any length (number of terms) from 1 to n-1. Here is an (2,2), (2,1)}, where all ring sums, taking modulo m1=3 for the first component of the vector-sums and modulo m2=4 for the second ones identifies the two-dimensional cyclic grid over 3x4 (Table 2).

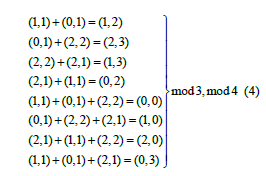
Table 2:Monolithic 2D IRB-code {(1,1), (0,1), (2,2), 2,1)} illustrates.

We can see that sequence {(1,1), (0,1), (2,2), 2,1)} forms complete set of ring code combinations on 2D ignorable array 3x4, and each of it occurs exactly once (R=1). Note, each of them forms massive arranged (solid parts of bits) both symbols “1” and of course “0” in the all-possible binary IRB-code combinations. This property makes monolithic IRB-codes useful in applications to coded design of signals for communications, control systems and vector data processing using limited number of bits for double (t=2) information content and higher correction speed. Applications profiting from multidimensional IRBs are for example electronics, low-side lobe antenna design [7], and big data processing [8].

Gloria to Ukraine Stars encoding systems

Figure 2: Planar projection of spatially disjointed ring axes m1=2 and m2=3 coordinate points of two- dimensional (t =2) toroid reference grid m1 × m2=2×3.

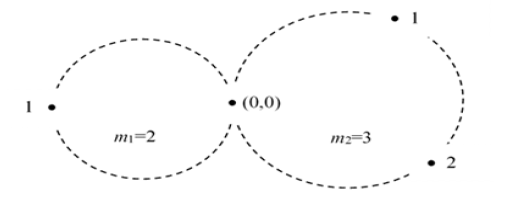
The idea of “perfect” encoding systems comes from remarkable properties of symmetry in nature laws [9]. A new type of IRBs is among the most perfect vector IRBs, which properties hold for the same set of the IRBs in varieties permutations of terms in the set (e.g. set of two-dimensional IRBs {(1,0), (1,1), (1,2), (1,3), (1,4)} and {(1,0), (1,2), (1,4), (1,1), (1,3)}. We call this vector combinatorial configurations “Gloria to Ukraine Stars”. Planar projection of spatially disjointed the ring axes m₁=2 and m₂=3 coordinate points of two-dimensional (t=2) toroid grid m₁ × m₂= 2 × 3 with common reference point (0,0) given in (Figure 2). We have designed toroid coordinate system for vector data coding two (t=2) attributes with two (m1=2) categories of the first, and three (m₂=3) for the second attribute accordingly. Clearly, for vector data coding t attributes and mi categories of each of them (i=1, 2, …, t) requires t concurrent disjointed axes m₁, m₂, …, mi, …, mt with common reference point forming t- dimensional coordinate grid of the system with sizes m₁ × m₂ ×… × m_t. So, the underlying multidimensional information manifold coordinate system can be described by parameters S, n, R, t, mi (i=1, 2, …, t). There are exist a priory numerous families of the GUS encoding systems [10].

Applications of the intelligent combinatorial configurations, namely the “Ideal Ring Bundles” (IRB)s, provide novel concept usages for finding optimal solutions for wide classes of technological problems, including mechatronic, vector encoding design, and multidimensional information technology with less number of elements than at present, while maintaining or improving on the other characteristics of the system. Gloria to Ukraine Stars (GUS)s encoding systems are well applicable for big vector data processing, electronic engineering and mechatronic, cyber-physics and robotics, intelligent information technologies, and other engineering areas.

1. Peterson WW, Weldon JE (1972) Error-Correcting Codes. (2^nd), The Massachusetts Institute of Technology, MIT Press, USA, pp. 576.
2. Robert McEliece (2002) The Theory of Information and Coding. (2^nd), California Institute of Technology, Cambridge University Press, UK, pp. 86.
3. Hall M Jr (1967) Combinatorial Theory. (1^st), Blaisell Publishing Company, USA, pp. 310.
4. Riznyk V (2017) Multi-modular optimum coding systems based on remarkable geometric properties of space. Advances in Intelligent Systems and Computing 512: 129-148.
5. Riznyk V, Bandyrska O (2008) Application of the gold ring bundles for innovative non-redundant radar or sonar systems. EPJ ST 154: 183-186.
6. (1976) Certificate of authorship, UK.
7. Riznyk V (1998) Multidimensional systems: Problems and solutions,” (Published Conference Proceedings style), London, pp. 1-5.
8. Cooperative Patent Classification G06f Electric Digital Data Processing.
9. Riznyk V (2006) A new vision of symmetry based on the ideal ring bundles theory. 9^th International Conference on Generative Art, Milano Polytechnico, Italy.
10. Riznyk V (2015) Multidimensional systems optimization developed from perfect torus groups. International Journal of Applied Mathematics and Informatics 9: 50-54.