- Submissions

Full Text
COJ Robotics & Artificial Intelligence
Modeling the Body Movements and Feelings of Humanoid Robots Using Fuzzy Logic
KahramanC* and Boltürk E
Department of Industrial Engineering, Turkey
*Corresponding author: Kahraman C, Department of Industrial Engineering, Turkey
Submission: October 01, 2020;Published: February 08, 2021

ISSN:2832-4463 Volume1 Issue3
Abstract
Robots having a body shape similar to the human body and resembling the human behaviors are called humanoid robots (HRs). They are assumed to improve the quality of human life in the future by performing human tasks such as assisting the sick and elderly people and doing dirty or dangerous jobs. They should perfectly resemble humans’ movements and feelings such as smiling, laughing, crying, getting surprised, getting sad, getting disgusted, or getting angry, if we really want to call them humanoid robots. Human feelings cannot be represented by 0-1 logic since an emotion can arise as different consequences of an infinite number of situations. Fuzzy logic is an infinite valued logic whose continuous values are between 0-1 and can be modeled by the fuzzy set theory introduced by Zadeh [1]. This paper provides ideas on how fuzzy set theory can be used to express human behavior and emotions in humanoid robots.
Keywords: Humanoid robot; Human feelings; Fuzzy logic; Fuzzy set theory; Intuitionistic fuzzy sets; Spherical fuzzy sets
Introduction
Humanoid robots imitate human feelings and human mechanisms of decision making and information processing. Several prototype humanoid robots for different purposes have been developed by various laboratories and universities. The first anthropomorphic intelligent robot WABOT (WAseda roBOT) was developed by Waseda University of Japan in 1973 (Figure 1). It had integrated systems for sensing, locomotion and manipulation inspired human capabilities. Later, Wabot-2 was developed in 1985 and it could play a piano. In 1986, Sony developed ASIMO, which was walking and climbing stairs. In 1993, MIT developed a humanoid robot having different but discrete facial expressions (sad, calm, surprised, etc.) and body components with different degree of freedoms.
Figure 1:Wabot.

Figure 2 illustrates some more recently developed humanoid robots. Sophia has been developed by Hong Kong based company Hanson Robotics in 2016. Sophia has only 60 different facial expressions. Kodomoroid developed by Hiroshi Ishiguro Laboratories in 2014 is a teleoperated humanoid robot resembling a human child. Jia developed by a Chinese team at the University of Science and Technology of China in Hefei could move her arms, create different facial expressions, and answer to human conversations. Mirai Madoka was developed by a Japanese tech Orix car rental agency in 2016. Junko Chihira is a humanoid developed at Toshiba having the ability to make human-like facial expressions. The vagueness and impreciseness in humans’ feelings and movements can be captured by the fuzzy set theory introduced by Zadeh [1]. In this theory, everything is a matter of degree and cannot be well defined by discrete logic. In the ordinary fuzzy sets, an element is determined by only a membership degree whereas an element in the extensions of ordinary fuzzy sets is determined by a membership degree and a non-membership degree, in which their sum is not necessarily equal to 1. The new extensions
Figure 2: Recently developed humanoid robots.

Using classical logic, you can only code feelings and movements that correspond to a certain number of events. However, people have completely different facial expressions and body movements in the face of countless different events. For example, a facial expression with tears of happiness and that with tears of losing a loved one are completely different. Besides, the tears of happiness when someone gets a marriage proposal and the tears of happiness of an athlete who finishes the marathon in the first place have completely different facial expressions. The answer to how these infinite numbers of cases can be modeled is of course the fuzzy set theory. The rest of the paper is organized as follows. Section 2 introduces the fuzzy set theory briefly. Section 3 presents the ideas on how fuzzy sets can be used in modeling the feelings and movements of humanoid robots. Section 4 includes the conclusions.
Fuzzy Set Theory
Fuzzy set theory found a wide application area in science and technology [2,3]. Decision making is one of the most attractive research areas with fuzzy sets [4,5]. Since ordinary fuzzy sets have been introduced by Zadeh [1], many extensions of them have appeared in the literature. Figure 3 illustrates the fuzzy set extensions with their historical order.
Figure 3:Fuzzy set extensions.
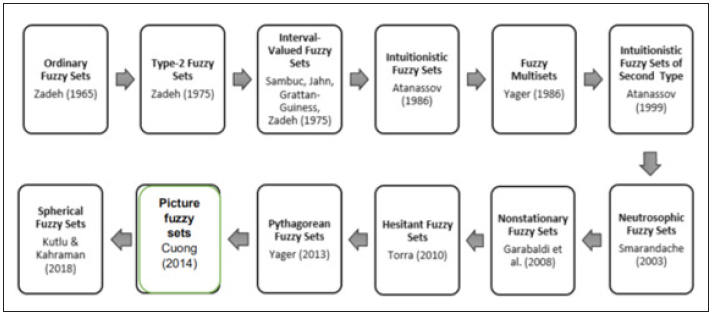
We can classify these recent extensions into two main groups:
a) Intuitionistic fuzzy sets and its extensions including
Pythagorean fuzzy sets, fermatean fuzzy sets, and q-rung
orthopair fuzzy sets,
b) Picture fuzzy sets and its extensions including spherical
fuzzy sets and t-spherical fuzzy sets. First group extensions
involve elements with one membership degree and one nonmembership
degree whose powered sum of them is at most
equal to 1 with a dependent hesitancy parameter.
Second group extensions involve elements with three
independent elements which are membership degree, nonmembership
degree, and a hesitancy degree whose powered sum
of them is at most equal to 1.
An ordinary fuzzy set A is represented by Equation (1):
A = {(x, μA (x))}| xε X (1)
where the function μA:X → [0,1] defines the degree of membership. An intuitionistic fuzzy set I in X is defined as in Equation (2):
Ĩ = {(x, μI(x), x νI(x)P)|xε X (2)
where the functions μI: X → [0,1] and ν1 : X → [0,1] define the degree of membership and the degree of non-membership of an element to the set I, respectively, with the condition that.
0 ≤ μI(x) +I(x) ≤1, for∀xε X
The degree of hesitancy is calculated as follows:
πI(x) = 1−μI(x) −νI(x) (4)
The second powers of the parameters in (3) and (4) yield Pythagorean fuzzy sets.
Picture fuzzy sets were introduced by Cuong [6]. A picture fuzzy set A on the universe X is defined as
Ã= {⟨ x; μI(x), ηA(x), ϑA (x)⟩|xε X} (5)
where μA(x) ∈ [0,1] is called the degree of positive membership of Ã; ηà ( x) [0,1] ∈ [0,1] is called the degree of neutral membership of à and ν à (x)∈[0,1] is called the degree of negative membership of à , satisfying the following condition.
0 ≤ μÃ( X ) +ηÃ( X ) +νÃ( X ) ≤1,∀Χ∈ X. (6)
Then for x∈ X, the degree of refusal membership of x in à is given as
πà (x) =1−μà (x) −ηà (x) −νà (x) (7)
The second powers of the parameters in (6) and (7) yield the spherical fuzzy sets.
Fuzzy Sets & Humanoid Robots
Figure 4:Smile and eye orb using mathematical functions.

The feelings and behaviors of a HR must be appropriate to the event it meets. Based on a discrete classification, humans have 21 different facial expressions. However, it is clear that this number is insufficient for representing infinite number of expressions of human feelings. Besides, the facial expressions are not universal and may change from a culture to another. Let’s assign membership and non-membership degrees of happiness for some examples of different feelings when intuitionistic fuzzy sets are used [7]. Assume that humanoid robots hear that “Your friend had a traffic accident.”, then the degree of feeling may be (0, 0.80). When it is “Your friend survived a traffic accident.”, then the degree of feeling may be (0.50, 0.35) or as an interval, ([0.40, 0.60], [0.30, 0.40]). When it is “Today is your friend’s birthday.”, then the degree of feeling may be (0.80, 0). When it is “Your friend died. “, then the degree of feeling may be (0, 0.90). When it is “Your friend died on his birthday.”, then the degree of feeling may be (0, 0.95). When it is “Your friend’s friend died.”, then the degree of feeling may be (0, 0.75) [8]. Mathematical relations for some of the most common facial expressions can be in the form of simple mathematical functions which can model expressions such as smiling, frowning and eyebrow raising. Using classical functions, the face expressions are tried to model as illustrated in Figure 4; [9]. As it is seen in Figure 4, feelings can be modeled by mathematical functions and the coefficients and constant values can be changed between two values in order to express the feelings from slight case to strong case such as slight anxious to strong anxious [10-13]. Linguistic terms can be best modeled by the extensions of fuzzy sets for this purpose. Let k be a coefficient as in Equations (8) and (9):
fsmilelower lip = −k cosx− 3.3, −2π / 3 ≤ x ≤ 2π / 3 (8)
fsmileupper lip = k cosx − 3.3, −π/ 2 ≤ x ≤π/ 2 (9)
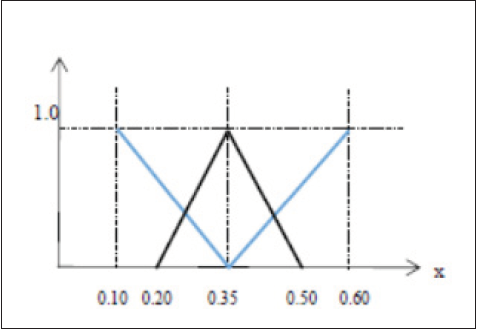
The coefficient k can be represented by an intuitionistic fuzzy
number as in Figure 5.
The function in Figure 5 can be represented by the following
α -cuts:
μL = 0.20+ 0.15α , μR = 0.50+ 0.15α
νL = 0.35− 0.25α, νR =0.35+ 0.25α
Figure 5:Intuitionistic fuzzy number for the coefficient
The fuzzy function between very slight smile and medium smile (vss&ms) then becomes.
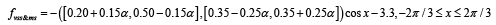
Conclusion
Research on humanoid robots is one of the most attractive topics in engineering today with the aim of producing autonomous humanoid robots thinking and moving like human beings. Classical logic approaches are not sufficient to model a humanoid robot as a copy of human being [16,17]. Continuous logic approaches should be used to capture the infinite number of feelings of human beings. Fuzzy sets try to define a problem under vague and imprecise environment. New extensions of fuzzy sets provide a more detailed membership function with additional new parameters. These parameters can be successfully used in modeling the humanlike behaviors of humanoid robots. Feelings and movements of humanoid robots can be directed by these membership functions much easier than classical control mechanisms [18,19].
References
- Zadeh LA (1965) Fuzzy sets. Information Control 8(3): 338-353.
- Kahraman C (2006) Fuzzy applications in industrial engineering. Springer, Germany.
- Kahraman C, Gulbay M, Kabak O (2006) Applications of fuzzy sets in industrial engineering: A topical classification. Fuzzy applications in industrial engineering pp. 1-55.
- Kaya I, Kahraman C (2009) Fuzzy robust process capability indices for risk assessment of air pollution. Stochastic Environmental Research and Risk Assessment 23(4): 529-541.
- Kaya I, Kahraman C (2010) Development of fuzzy process accuracy index for decision making problems. Information Sciences 180(6): 861-872.
- Cuong BC (2014) Picture fuzzy sets. Journal of Computer Science and Cybernetics 30(4): 409-420.
- Atanassov KT (1999) Intuitionistic fuzzy sets: Theory and applications, studies in fuzziness and soft computing.
- Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy sets and Systems 20(1): 87-96.
- Garibaldi JM, Ozen T (2007) Uncertain fuzzy reasoning: A case study in modelling expert decision making. IEEE Transactions on Fuzzy Systems 15(1): 16-30.
- Guinness GI (1976) Fuzzy membership mapped onto intervals and many-valued quantities. Logik und Grundlagen Math 22(1): 149-160.
- Jahn KU (1975) Intervall-wertige mengen. Math Nach 68(1): 115-132.
- Gündoğdu KF, Kahraman C (2019) Spherical fuzzy sets and spherical fuzzy TOPSIS method. Journal of Intelligent and Fuzzy Systems 36(1): 337-352.
- Sambuc R (1975) Function Φ- Application to aid in diagnosis in thyroid pathology. University of Marseille, France.
- Smarandache F (1999) A unifying field in logics. Neutrosophic Logic. American Research Press, Rehoboth, USA.
- Torra V (2010) Hesitant fuzzy sets. International Journal of Intelligent Systems 25(6): 529-539.
- https://www.desmos.com/calculator/25oi4snhve
- Yager RR (1986) On the theory of bags. International Journal of General System 13(1): 23-37.
- Yager RR (2013) Pythagorean fuzzy subsets. Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Canada.
- Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning. Information Sciences 8(3): 199-249.
© 2021 KahramanC. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






