Assessment of Vaccination Coverage Required for Covid-19 Incidence Control

The pandemic of a new infectious disease caused by the COVID-19 pathogen has become a significant factor affecting the life and well-being of the population of the world as a whole. China’s experience has shown that the incidence of new coronavirus infection can be successfully controlled by intensive measures if applied severely, which the public in most countries does not agree with. Therefore, so much hope goes with the vaccine, which is being developed in a number of research centers. If vaccination is used as anti-epidemic measures and the proportion of those who have protective immunity as a result of vaccination is V, the average number of r persons infected through one infected is equal to 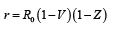where Z is the level of collective immune status obtained as a result of infecting with the pathogen [1]. Consequently, in order for the incidence to decrease, it is prerequisite, that 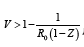and to further control the spread of the pathogen in the absence of natural collective immunity 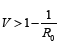It is worth mentioning here that V is not coverage of vaccinations, but the proportion of the population that has a protective titer of antibodies, and the ratios are obtained by vaccination in equal proportions without regard to risk groups (at risk infection and individual contagion) and without serological control (latent cases show no immunization). The resulting expressions give only a minimum level for vaccination, which is desirable to be surpassed, as in case of “protection without reserve” cases brought from abroad will cause quite a lot of contact affectioning. The average number of contact cases from one brought will be equal to 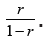For example, if the contact number is 2.5, the minimum proportion of the population that needs to become immune is 60%. If immunity is created in 70%, then 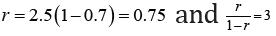that is, each brought case will account for an average of 3 contact cases.

a) It is sufficient to accurately estimate the contact number R0 [2-4]

b) Assess the structure of risk groups [2].

The value of the contact number can be estimated by the dynamics of the incidence. The dynamics of incidence are determined by the current number of infected persons, the level of collective immune status, and the activity of the transmission mechanism. Quantitative characteristic of activity- contact number R0, which is a characteristic of interaction between pathogen and host populations “here and now”, varies in different populations and changes over time. The value of the contact number changes due to the carrying out of anti-epidemic measures, as well as “seasonal factors”-the dependence of the transmission mechanism activity from the time of year.

Within the SIR model of the epidemic [1], the dynamics of the number of infected I and susceptible S is given by the equations

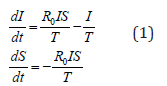
where T is the average duration of the disease (more precisely - the infectious process, from affectioning to cessation of pathogen release.

At the initial stage of the epidemic, when the collective immune status has not yet been developed and S is close to one, the proportion of infected grows I (t) = ce^λt exponentially rate of exponential growth and the contact number are correlated as R₀=1+^λT . For example, if the number of new cases increases per day by an average of 5%, and the duration of the disease is 10 days I (t ) = ce^λt , we have. For the example given λ = ln (1.05) ≈ 0.04879 and R0≈1.4879.

For the period from March 31 to May 15 (the period of antiepidemic measures of moderate intensity), the average exponential growth rate for Moscow was λ≈0.0735, for Russia excluding Moscow λ≈0.0958 and for Brazil λ≈0.0389, which corresponds to a 7.63%, 10.05% and 3.97% increase in the number of patients per day, respectively. If the average duration of the disease is 10 days, we have for Moscow R₀≈1.735, for Russia except for Moscow R₀≈1.958 and for Brazil R₀≈1.398.

There are two shortcomings in the presented calculation scheme:

a) The average value of the contact number over a long period is estimated, whereas due to the active countermeasures to the propagation of the pathogen, the situation may change significantly in a few days,

b) The concept of “average duration of the disease” is too vague to accurately determine the value of the contact number [3]. In the simplest model, it is believed that the contagion rate of an infected person is constant, whereas immediately after affectioning there is a sterile period. After it, the release of the pathogen increases, then (in case of recovery) it decreases. In addition to changes in pathogen release activity and social activity changes as well, which decreases after the appearance of pronounced symptoms. In this regard, it is advisable to take into account the change in contagion hazards during the infectious process.

Then if K(n), n=1,2,... the relative average is required in n days after infection K(1)+K(2)+...=1, then the dynamics of the number of infected per day N is given by the equation

A(N) = R ₀ (A(N − 1)K(1) + A(N − 2)K(2) + ....)

Then the current value of the contact number on the day N is defined as

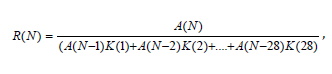
where A (n) is the number of cases on the day number n.

As a result, we have that in spring the contact number for Russia and Moscow was larger than one, but was decreasing, corresponding to the increase in incidence with the decrease in the rate of exponential growth. For most of the summer, the contact number for Moscow was slightly smaller than one, which corresponds to a gradual decrease in incidence, and for Russia excluding Moscow-it was about one, which corresponds to constant morbidity. Since the end of summer, the contact number for Moscow has been growing, exceeded one and is continuing to increase, giving growth at a rate above exponential.

For further analysis, we take into account that the value of the contact number is affected by the seasonal factor and accumulation of collective immunity, so that

whereR ̄0 is the “base” value of the contact number estimated above S(t) is the proportion of the susceptible part of the population E(t) is the reduction in transmission activity thanks to effectiveness of the anti - epidemic measures and G(t) is seasonal fluctuations in the activity of the transmission mechanism, that is, a positive function with a period of one year and an average of 1.

To estimate the magnitude of G (t), let’s take the model of the epidemic process

Where T_max is life expectancy (for infections with temporary immunity-duration of immunity). B for community-acquired pneumonias in Russia during the year, the incidence changes about 4 times. Taking b [3,4] the average duration of the disease as 10 days, we get that the quadruple fluctuation of the incidence will show sinusoidal fluctuations G (t) with an amplitude of about 10%. Thus, the change in the activity of the transmission mechanism over the spring/summer and summer-autumn period can be estimated at 10%. Of course, this is quite a rough estimate, but it gives an approximate value of seasonal variations. “Seasonal factor” has reduced incidence for summer by 3.5-4 times. Its “strength” is sufficient to significantly change the situation, but not enough to eliminate the pathogen-the contagion of COVID-19 is too great. The third component of the expression [2] is the proportion of susceptible S (t). Based on the statements made about the results of screening studies of Moscow residents, the proportion of seropositive cases currently stands at about 25%. If we do not consider the presence of risk groups, 25% of seropositive Muscovites gives a reduction in pathogen transmission activity by a quarter.

Finally we have, that if by the end of summer the contact number in Moscow was about one, having in mind that the decrease due to seasonal factor is 10%, and due to accumulation of collective immunity is 25%, it totals, excluding these two factors, that the contact number would be about 1.5, meaning the situation in Moscow now would correspond to mid-April. That is, if all antiepidemic measures are completely lifted (that is, the contact number will return to the level of 2.6), the minimum level of vaccination (without serological control) for Moscow shall be 48.7%.

If vaccination is carried out only for seronegative population, it will be necessary to “vaccinate” 36.5%. Estimates are obtained without taking into account the structure of risk groups If highrisk groups are first vaccinated, vaccination will be more effective, but the high-risk group for COVID-19 are older people whose vaccination is quite difficult. If disease and vaccination do lead to temporary immunity, it is necessary to immunize more than 62% of the population by the vaccine. However, it should be noted that these estimates are not vaccination coverage, but the proportion of populations that have protected immunity as a result of vaccination. In addition, it is a minimum level, and at the actual level of collective immune status slightly above the minimum, cases brought cause a large number of contact infecting.

1. Roy MA, Robert M, Anderson B (1992) Infectious diseases of humans: Dynamics and control our oxford.
2. Giordano G, Blanchini F, Bruno R, Colaneri P, Filippo A, et al. (2020) Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Medicine 26: 855.
3. Lauer SA, Grantz KH, Jones FK, Zheng Q, Meredith HR, et al. (2020) The incubation period of coronavirus disease 2019 (covid-19) from publicly reported confirmed cases: Estimation and application. Ann Intern Med 172(9): 577-582.
4. Liu Y, Gayle AA, Wilder SA, Rocklöv J (2020) The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Travel Med 27(2): 1.