Modeling with Hyperbolic Restrictions: The Nigerian Population Dynamics

In demographics, an intercensal estimate is an estimate of population between official census dates with both census counts being known. Some nations produce regular intercensal estimates while others do not. Intercensal estimates can be less or more informative than official census figures, depending on methodology, completeness, accuracy (as they can have significant undercounts or overestimates) and date of data, and can be released by nations, subnational entities, or other organizations including those not affiliated with governments. Being able to forecast population and even being able to answer some interesting questions about population in the past, depends on developing accurate mathematical models of population growth. Analysis and projection of population are based on population figure as it informs an objective distribution of social amenities by government. Hence, knowledge about past, current and future population are fundamental in every aspect of decision making. In view of this, current projection of this population figures is of great necessity. Ofori et al. [1] applied exponential and logistic growth models to model the population growth of Ghana using data from 1960 to 2011. Dean Hathout [2] modelled population growth using exponential and hyperbolic models. Oyamakin et.al [3,4] compare exponential and hyperbolic growth models in height and diameter increment of Pine (Pinus caribaea).The aim of this study is to investigate the property of Exponential Growth Model (EGM) and Hyperbolic Exponential Growth Model (HEGM) in modeling Nigeria population data and to determine the intercensal estimate, and compare the predictive performance of the two models.

Data description

The Nigeria population census figure for the year 1963, 1991 and 2006 were used for intercensal prediction and nonlinear estimation was applied on the data sourced online [5] from 1955-2016 for model validation. Intercensal estimation was observed for three cases using three growth models. Cases 1 was the use of the 1963 population census result as the base year and 1991 population census result as the launch year, case 2 was the use of the 1991 population census result as the base year and 2006 population census result as the launch year and case 3 was the use of the 1963 population census result as the base year and 2006 population census result as the launch year.

Methodology

Exponential Growth Model (EGM)Suppose that Pt is the total number of individuals in the population at time (t) such that;

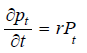(1)

Separating variables, we have that;

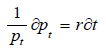(2)

Integrating both sides we have;

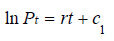(3)

Taking the exponential of both sides we have;

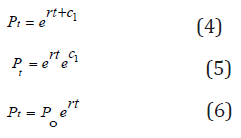
The growth rate will be

(7)

Equation (6) is the Exponential Growth Model

Hyperbolic Exponential Growth Model (HEGM) Studies have shown that majority of the growth models emanated from the Malthusian Growth Equation (MGE), which is limited to growing without bounds. This study was designed to develop alternative growth models flexible to enhance internal prediction of population figures based on hyperbolic sine function with bound. Suppose that Pt is the total number of individuals in the population at time (t) such that;

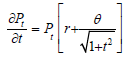(8)

Separating variables, we have that;

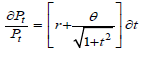(9)

Integrating both sides we have;

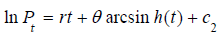(10)

Taking the exponential of both sides we have;

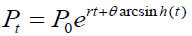(11)

The growth rate will be

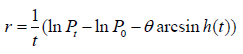(12)

Equation (11) is the Hyperbolic Exponential Growth Model

Where P0 is the population value for the base year, Pt is the population value for the target year, is the shape parameter which act as a stabilizing factor and can take both negative and positive value depending on the intrinsic nature of the growth rate.

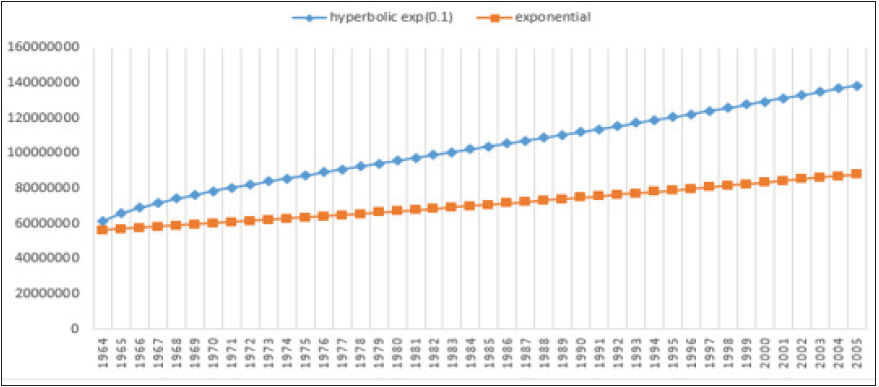
Hyperbolic exponential growth rate was used for intercensal estimation using different values of theta which ranges from small to moderate to high with ±0.1, ±0.5 and ±0.9. Theta can take positive value if the growth rate of a population is low and it can take negative value if the growth rate of a population is high, therefore theta is said to be a stabilizing factor. In Table 1, the growth rate estimate for different cases using Geometry Growth model (GGM), EGM and HEGM. HEGM with theta (0.5) and (0.9) produced negative growth rate for the three cases and the implication of this is that human population is going into extinction. Figure 1-3 suggested that EGM and GGM predicted the same intercensal estimate for the three cases, which prompted us to compare the HEGM with the EGM. Figure 4-6 present the intercensal estimate using HEGM with theta (0.1), (-0.1), (-0.5) and (-0.9) for the three cases. For case 1 and 2, HEGM with theta (0.1) performed best, followed by HEGM with theta (-0.1), theta (-0.5) and theta (-0.9) while for case 3, HEGM with theta (0.1) performed best, followed by HEGM with theta (-0.1) and theta (-0.9). Figure 7 suggested that HEGM with theta (-0.5) does not converge. Figure 8-10 suggested that HEGM with theta (0.1) performed better than EGM in predicting the intercensal estimate for the three cases. Table 2,3 present the result of the nonlinear estimation and the fitted exponential and hyperbolic exponential growth model were = 38.849262e^0.025675t and = 41.14675e^{0.025675t – 0.0215562arcsinh(t)} respectively. In Table 4, the hyperbolic exponential growth model was preferred based on the AIC, BIC and MSE results given as -11.8753, -10.18044 and 0.9571 respectively.

Table 1:Growth rates for different cases based on the models

Source: Computed by the authors

* indicates values of the shape parameter that produces negative growth rate

Table 2:Parameter estimation using HEGM

Source: Computed by the authors from data sourced from (www.worldometers.info)

Table 3:Parameter estimation using EGM

Source: Computed by the authors from data sourced from (www.worldometers.info)

Table 4:Selection criteria

Source: Computed by the authors

Figure 1:Intercensal estimate for case 2 using geometry and EGM

Figure 2:Intercensal estimate for case 3 using geometry and EGM

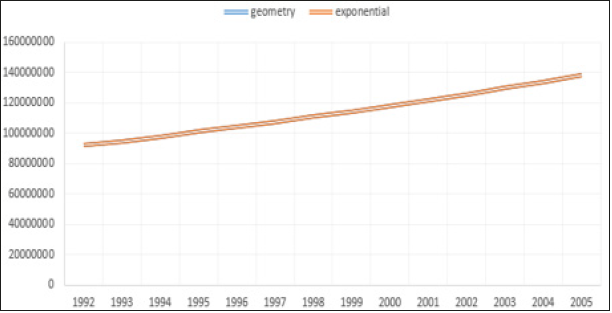
Figure 3:

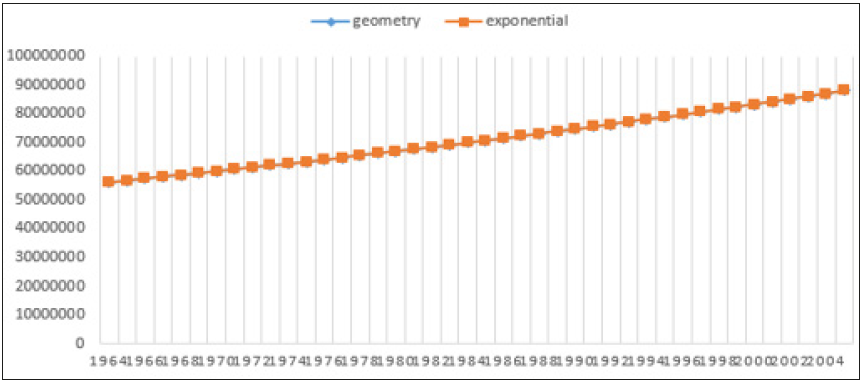
Figure 4:Intercensal estimate for case 1 using HEGM with (0.1), (-0.1), (-0.5) and (-0.9)

Figure 5:Intercensal estimate for case 2 using HEGM with (0.1), (-0.1), (-0.5) and (-0.9)

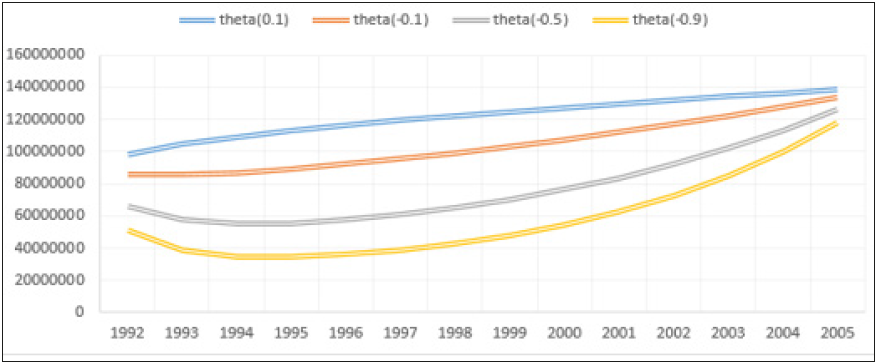
Figure 6:Intercensal estimate for case 3 using HEGM with (0.1), (-0.1) and (-0.9)

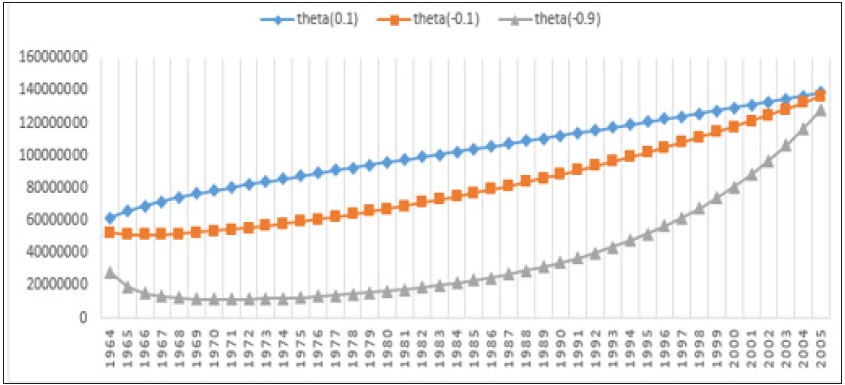
Figure 7:Intercensal estimate for case 3 using HEGM with (0.1), (-0.1), (-0.5) and (-0.9)

Figure 8:Intercensal estimate for case 1 using EGM and HEGM ( (0.1))

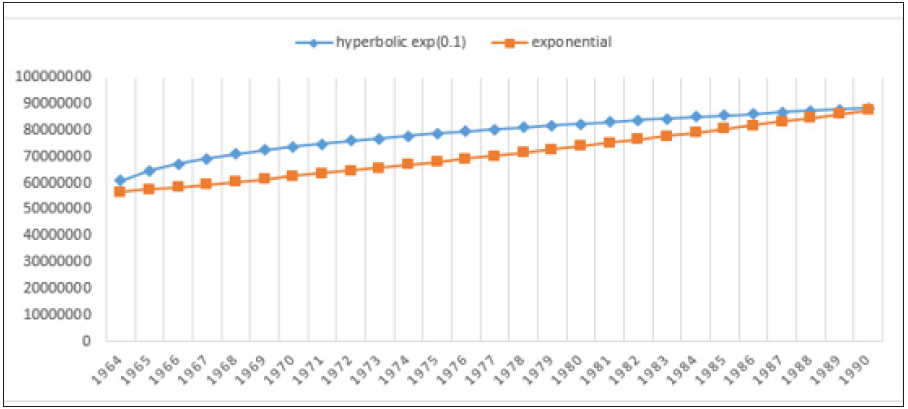
Figure 9:Intercensal estimate for case 2 using EGM and HEGM ( (0.1))

Figure 10:Intercensal estimate for case 3 using EGM and HEGM ( (0.1))

Different values of theta in the hyperbolic model were assumed to be small, moderate and high with ±0.1, ±0.5 and ±0.9 respectively for Case 1, 2, and 3. HEGM gave the best intercensal estimate for the three cases and was preferred based on the AIC, BIC and MSE results with theta stabilized at ±0.1.

1. Ofori TL, Ephraim, Nyarko F (2013) Mathematical Model of Ghana's Population Growth. International journal of modern management sciences 2(2): 57-66.
2. Dean Hathout (2013) Modeling population growth, exponential and hyperbolic modeling. Applied Mathematics 4: 299-304.
3. Oyamakin SO, Chukwu AU, Bamiduro TA (2013) On comparison of exponential and hyperbolic exponential growth models in height/diameter increment of PINES (Pinus caribaea). Journal of modern applied statistical methods 12(2).
4. worldometers.info
5. Sintayehu AM (2016) Mathematical model of ethiopia's population growth. Journal of natural sciences research 6(17): 1015-116.