Control of Dog Rabies Disease Infection with the Approach of Culling and Vaccination Interventions

Rabies is a Lyssavirus zoonotic carnivore’s disease which was discovered since the year 3000BC in the Sanskrit name rabhas which means violence. It has been known for ages, more than 4300 years in which it becomes slowly spreading among many countries and across number of regions [1-33]. Rabies disease causes human deaths which is estimated to about 59,000 per year globally [8,15,32], in which around 36.4% occurring in Africa and 59.6% in Asia [24,29-38]. According to WHO [39], in African region, about 21,000 human deaths cases occur annually due to this disease. In East African region, the early cases were identified in Kenya at Machakosi District around the year 1912 [6]. However, several measures were taken against the disease, but its induced death rate in the region is still increasing from 4,400 to 6,500 for dog and from 210 to 290 for human-populations per year [5].

Apart from dogs, rabies disease affects other animals such as cats, foxes, skunks, raccoons, and other mammal virus carriers [33]. Dogs remain the major carrier for the rabies disease transmission to humans even to other animals as well [8,24,32]. The disease is mostly transmitted through virus-laden saliva of a rabid or infected dog through biting or contamination with virus infected saliva on the broken skin or wound or scratches among the animals or dogs [1,39]. According to Addo [1], the motor pathway is the major and primary media through which rabies virus path through to the spinal cord where it becomes affected and quickly moves to the central nervous system. Once the infections reach the brain, several behavioural changes emerged up due to defections of neurons. The defection of nervous system leads to brain inflammation to an organism and therefore death will be the final results.

Vaccination and treatment is among control measures for dog rabies disease spreading. Vaccination for rabies disease in dog or canine populations, are introduced in susceptible population group through either oral or injection way [39]. This will give more protection to susceptible dogs which are likely to be infected when interacting with infected dog(s). Theoretically and empirically, vaccination is considered as effective when coverage covers about 70% of the dog population [32]. On the other hand, treatment is imposed to an exposed population group after dog or canine bite occurs from the suspect rabid dog before infectious stage developed [14]. This secures all bitten dogs which have not yet develop disease infection symptoms, but as symptoms appeared no any more treated for infected dog and eventually dies out [33]. In any case of dog bite or any suspected rabid animal, all wounds or scratches injuries should be cleaned and washed thoroughly immediately with soap and clean sufficient amount of water for about 15 minutes including a supportive care to a victim [37]. Rabies disease remains burden to many areas which leads to animal and human deaths, decrease human productivity due to mortality or disability, incurring costs for vaccination and treatment programs [39]. The disease is still dominating in animal and human populations, especially young age groups [18], and therefore more efforts are needed to minimize the disease spread and deaths.

Mathematical models have proved to be valuable tools for better understanding the biological stability of infectious diseases in a host, its transmission dynamics in a community, and the establishment of relevant disease control plans [27]. The following are some works done about the disease infection with different intervention strategies.

Addo [1] studied SEIR model for rabies transmission disease in dog population group with vaccination at Bongo District, Ghana. Simulation showed that basic reproduction number, R₀ with vaccination is 0.3755 implies R₀ < 1 while without vaccination was 1.3267 which indicates R₀ > 1 thus endemic status, and 24.6% was the minimum population coverage of dogs to be vaccinated. Tulu [36], presented similar model with extension SEI1I2R (Susceptible- Exposed Prodromal Infectious-Furious Infectious-Recovery) with importation of infected immigrants for rabies transmission in dog population using vaccination as the disease control measure. In the studies by Carroll [7], Ward Carrollet [37] and Laager [20], a Susceptible Vaccinated Exposed Infectious (SVEI) model compartments was developed for the transmission of rabies among dog population using immune-contraception approach to pause dog populations in towns and cities through vaccination with dog fertility birth control or surgical sterilization which reduces newborn puppies. Again, Kitala [19] proposed a model with classes Susceptible Vaccination Latent Infectious (SVLI) for transmission of dog rabies disease with vaccination control strategies in a closed dog population group at Machakos District in Kenya. Apart from sensitivities analysis done, vaccination was considered as the most effective measure to control the disease spread among dogs.

Furthermore, in the work by Fitzpatrik et al. [12] and Bilinski et al. [4], SVEI model was presented with vaccination campaign for rabies transmission in which cost effectiveness was discussed on Carnivores vaccination for preventing rabies disease spread in Serengeti and Ngorongoro districts in Tanzania by dealing with dog and other wildlife population groups. Also, Ndii et al. [28] developed similar model by using crisp and fuzzy approaches in which vaccination provision and infection transmission rate considered as major aspect in transmission. Leung & Davis [22] proposed SVEI model for supplying vaccination on rabies disease control to stray, free-roaming and owned dog population. In similar way Asamoah et al. [3] and Wiraningsih et al. [38], developed and analysed SEIR model while Yang & Lou [40] formulated SVEI model for rabies disease transmission dynamics between dog-human interacting groups with vaccination control measures. Again, Ega et al. [10], presented similar SEIR model with interaction of dog-human-livestock population groups on rabies transmission analysis using vaccination intervention in Addis Ababa, Ethiopia, while in Huang et al. [16], similar model was developed for rabies transmission dynamics but with dog-human-chinese ferret badger interacting population groups in Zhenjiang Province, China.

However, Tian et al. [34] researched on re-emergence of rabies disease transmission dynamics for domestic dogs in Yunnan province [41], China and modeled SVEI for dog-human interacting populations using vaccination control approach with environmental factors. Additionally, Zinsstag et al. [42] constructed SVEI model with vaccination in dog’s group for eliminating rabies transmission from dog-to-human interacting populations in N’Djamena, Chad. In their study vaccination was incorporated as potential method for the disease prevention.

Therefore, the current work proposed and analysed mathematical model incorporated with vaccination and culling intervention stretegies to control the spread of dog rabies disease infection in the dog population. The model consists of Susceptible- Vaccinated-Exposed-Infectious-Recovery (SVEIR) compartments for the purpose of minimizing dog rabies disease transmission in dog population alone by dealing with vaccination in susceptible and exposed groups while practice culling for latent or exposed and infected classes on the other side as the major carriers and transmitters of the disease.

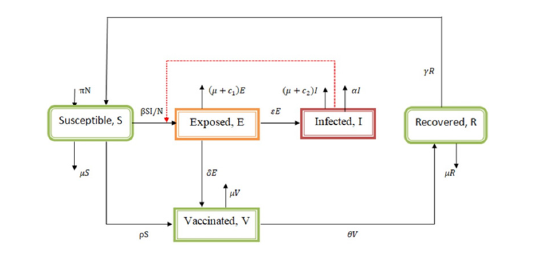
Model formulation

In this part a Susceptible-Vaccinated-Exposed-Infectious- Recovery (SVEIR) model is formulated. Susceptible dogs S are those which are healthy but are likely to be infected when interacting with the infectious, while Exposed dogs E these are the population which have not yet shown the symptoms. Infected dogs I is a group whose disease infection symptoms developed and Recovered dogs R is the group which get immunity due to either vaccination or treatment. In the present paper vaccination V, is introduced to the susceptible and exposed dog populations to give more protection against suspected rabid dogs once they interact while treatment is initiated in the exposed dog population, E_d, to rescue all bitten dogs by rabid or suspected rabid dogs but before developing any clinical symptoms of the disease infection. In developing the model, we considered the assumptions that, dogs are mixing each other in random way and such that there are equal chance of the infection transmission occurs from infected dog I to the susceptible dog S through direct contacts. We considered the following parameters and assumptions.
I. The infection rate of dog rabies disease in dog population occurs at the rate of β.
II. The recruitment rate of dog population occurs at the susceptible population group S at the rate of π.
III. Vaccination is supplied to the susceptible and exposed dog populations S and E at the rate of ρ and δ respectively, in which some gain temporary immunity and hence goes to recovered class R with the rate θ.
IV. Dog population decreases due to disease deaths rate at α and natural mortality rate, μ and disease induced death rate of α. V. The exposed dog population E gains infection through ϵ and joining the infected group I. In both, exposed and infected classes culling practices c1 and c2 are introduced to control their birth rates or population increase respectively.
VI. The recovered dog population R goes to the susceptible population group S through the rate of γ when the immunity wanes.

From Figure 1 & 2, a set non-linear ordinary differential equations showing dog rabies disease dynamics in the dog population compartments were formulated.

Figure 1:Panel (A) Represents a dog been infected with rabies disease while (B) Is vaccination service provision.

Figure 2:Dog rabies disease model flow chart.

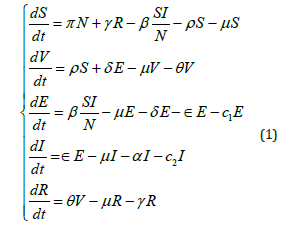
Positivity and boundedness of the model,/

For the biological model involving population to be meaningful, it must be bounded and non-negative invariant. Thus we verify this in the following procedures. From equation (1) we have

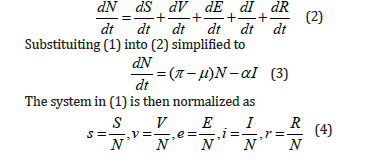
such that

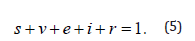
Substituiting (4) into (3) becomes

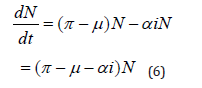
Taking derivative in (4), then the system in (1) become dimensionless as

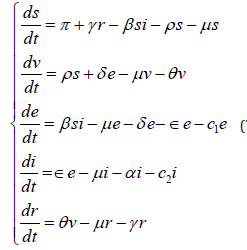
subject to

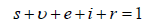
Thus, it is sufficient to show that, all feasible solutions of (7) is contained in the system (1) defined by

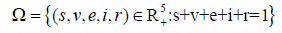
Therefore, the system in (7) is bounded with positive invariant which is biologically well posed and defined [21].

Disease free equilibrium point

Solving equations in (7) with respect to its variables, diseasefree equilibrium point E₀ is found as:

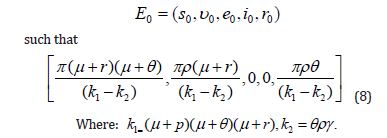
Basic reproduction number, R₀

Basic reproduction number R₀ refers to an average number of secondary infected individuals produced from an initial single primary infected individual in its lifetime duration when introduced in the host population in the absence of intervention [25]. The basic reproduction number, R₀ is very important quantity for analysing epidemiological models for disease control, which gives the following interpretations: For R₀ < 1, it means the average number of secondary infections produced by a single primarily infected individual is below the unity value, thus, the disease dies out [25]. Similarly, for R₀ = 1 implies threshold value in which the average number of secondary infected individual produced by the primarily infected one is constant proportion, hence the disease dies also [27]. Conversely, if R₀ > 1, then the number of secondary infected individuals produced by a single primarily infected one is above the unity (threshold) value during its entire time of infectiousness, therefore, the disease becomes epidemic in the population [27]. Castillo-Chavez, Feng, and Huang approach as in Martcheva [23] was used to compute R₀ in which is found as

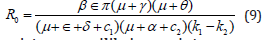
Dog rabies existence equilibrium point

Let E* defines dog rabies disease dominating equilibrium point, then by solving the system in (7) the endemic equilibrium point is found as;

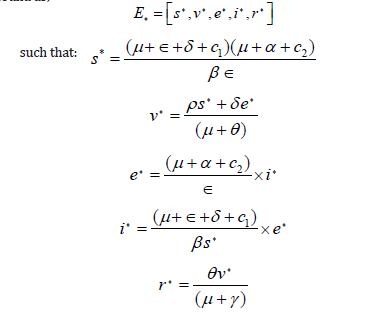
Local stability of non-existence dog rabies disease equilibrium point E₀

To determine the local stability of the non-existence dog rabies disease equilibrium point, we linearize the system set (7) in which we get Jacobian Matrix J(E₀) at E₀ as;

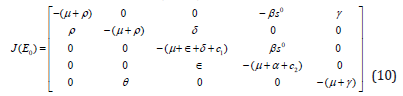
Then from the linearized matrix in equation (10), The tracedetermint technique is used [10], in which it gives;

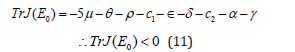
Again, from equation (10) the determinant Det J(E₀) is given by

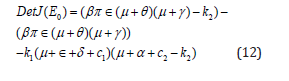
By simplifying, rearranging and use the relation in equations (9) and (12) we finally get;

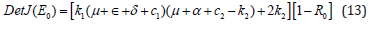
But for the determinant Det J(E0)>0, it follows that

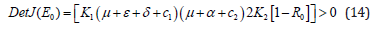
By considering condition in equation (14) that, Det J(E₀) > 0 for R₀ < 1, then it follows that, biologically, dog rabies disease will be leaving out from the dog population. This leads to the following theorem 1 that;

Theorem 1. If R₀<1, then the disease free equilibrium point E₀ is locally asymptotically stable, while unstable for R₀>1 in the region Ω.

Global stability analysis of non-existence of dog rabies disease equilibrium point

In determining the global stability of E₀, Lyapunov function approach is used [3,17,31]. This needs to prove theorem 2 that;

Theorem 2. If R₀ ≤ 1, then the disease-free equilibrium point E0 is globally asymptotically stable, while for R₀ > 1 will be unstable in the region Ω.

Proof: The Lyapunov function W with non-negative coefficients b₁ and b₂ in the trivial equilibrium points E₀ is chosen such that;

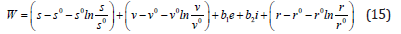
By differentiating with respect to time t in equation (15) we get;

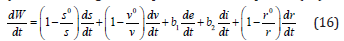
By substituting equation (2) into (16) it becomes;

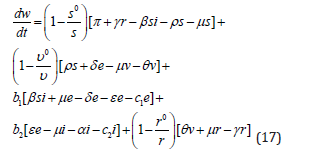
Without loss of generality, suppose that; s ≤ s⁰, υ ≤ υ⁰ and r ≤ r⁰ then by substituting in equation (17) and simplify leading to;

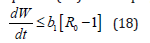
Thus, from equation (17) it is clear that, the largest invariant positive compact set in {(s, υ, e, i, r) ∈Ω}such that dw/dt≤0 , is the singleton set of E0 of the system (7) for R₀ ≤ 1. Therefore, according to Lasalle’s invariant principle (Murray et al, 1993), the disease-free equilibrium point, E₀ of the system in (7) is globally asymptotically stable in the region Ω for R₀ ≤ 1 and unstable for R₀ > 1. Hence this completes the proof of the theorem 4 above.

Global Stability Analysis of Dog Rabies Disease Existence Equilibrium Point: Global stability of endemic equilibrium point E* was determined by using the Lyapunov function technique [3,31]. This is done by proving that the Lyapunov function L as follows,

Proof:

Suppose R₀ > 1, in which E* exists, then to prove the global stability, we define and derive the 5Lyapunov function L as follows;

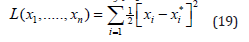
Where: X_i = dog population classes (s, υ, e, i, r) and X_i*= dog rabies disease dominated equilibrium point, E_∗. From the system in equation (7), then (19) becomes;

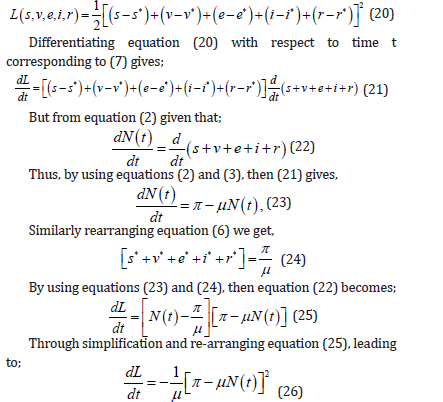
Thus, from equation (26), it is clear that, dL/dt<0 is a strictly Lyapunov function which implies that, the endemic equilibrium point E_∗ is globally asymptotically stable contained in the region Ω.

Biologically this implies that, dog rabies disease is stable and will be able to invade dog population for a long time.

Also, from equation (26), dL/dt=0 = if we set s = s∗, υ = υ* , e = e∗, i = i* and r = r*. Hence,dL/dt converges in positive region Ω as t →∞. Thus, this leads to the proof of the theorem 3 that,

Theorem 3. If R₀ > 1, then the endemic equilibrium point is globally asymptotically stable contained in region Ω.

Numerical Simulations and Discussion

This section presents the numerical simulations of the variables and parameter values with the support of MATLAB software. The parameter values were chosen randomly from previous studies as indicated in the Table 1 below, while the initial conditions of the dog population compartments were estimated as Susceptible S = 1,000, Vaccinated V = 600, Exposed E = 300, Infected I = 100 and Recovered R = 200 to justify the proposed study.

Table 1: Parameter Values of the Model.

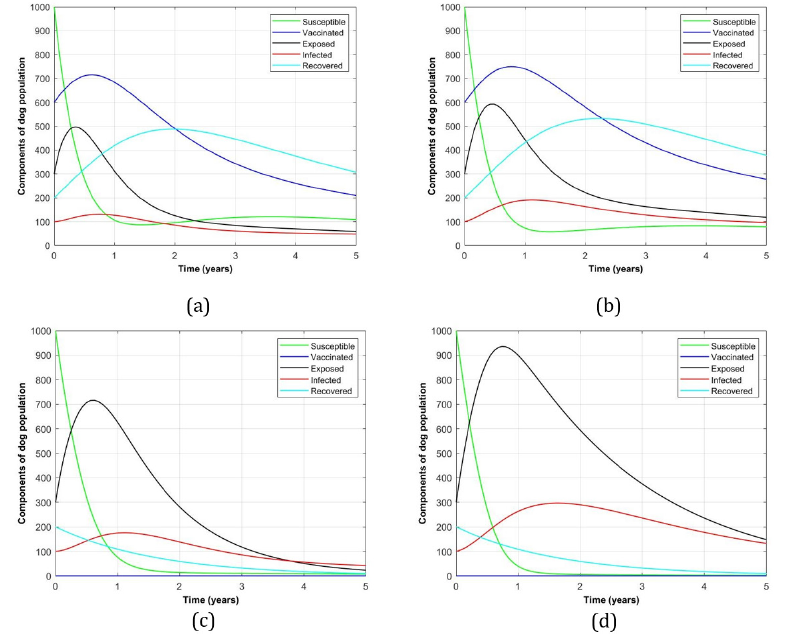
Figure 3 shows dog population profile that, (a) and (d) present the presence and absence of both, vaccination and culling dog rabies disease interventions respectively. While panels (b) and (c) indicate the presence of single intervention in each but with the absence of culling and vaccination respectively.

Figure 3:Profile of dog population with and without the vaccination and culling disease interventions.

Impact of vaccination intervention alone for rabies disease control in dog population: Figure 4 shows dog population profile in presence of vaccination intervention alone. Panels (a) and (d) indicate decrease and increase of susceptible and recovered dogs as more vaccination rates were increasing respectively. On the other hand, (b) and (c) represent the exposed and infected dog groups for which as more vaccination rates were administered to both, the more dogs were reduced from their respective classes and vice versa.

Figure 4:Profile of dog population with the variation of vaccination rate intervention alone.

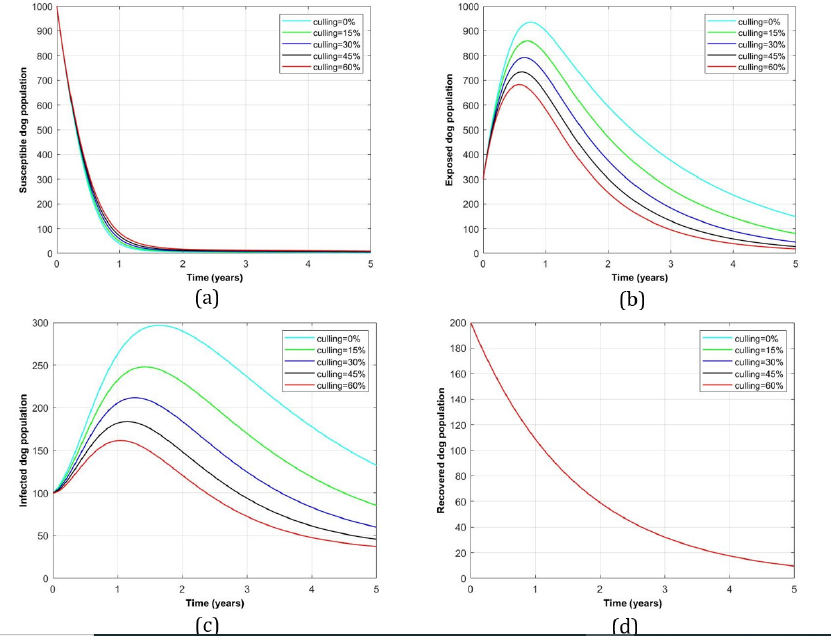
Impact of culling intervention alone for rabies disease control in dog population: Figure 5 indicates dog population profile in the existence of culling practice intervention alone. Panels (a) and (d) show the insignificantly decrease or change of both susceptible and recovered dogs as more culling rates were handled. On the other hand, (b) and (c) represent the exposed and infected dog groups for which there were potentially reduced number of dogs as more culling rates were introduced to both and vice versa.

Figure 5:Profile of dog population with the variation of culling rates intervention alone.

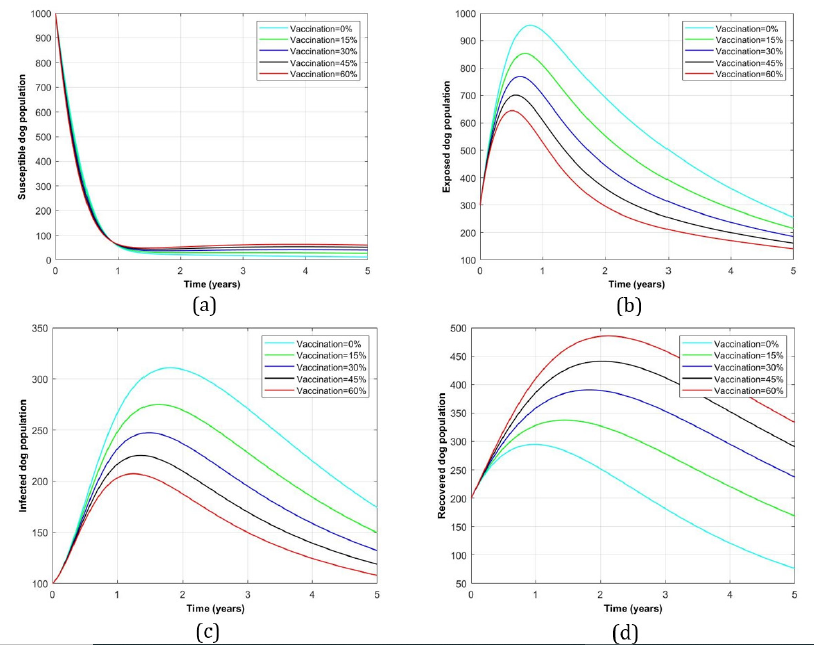
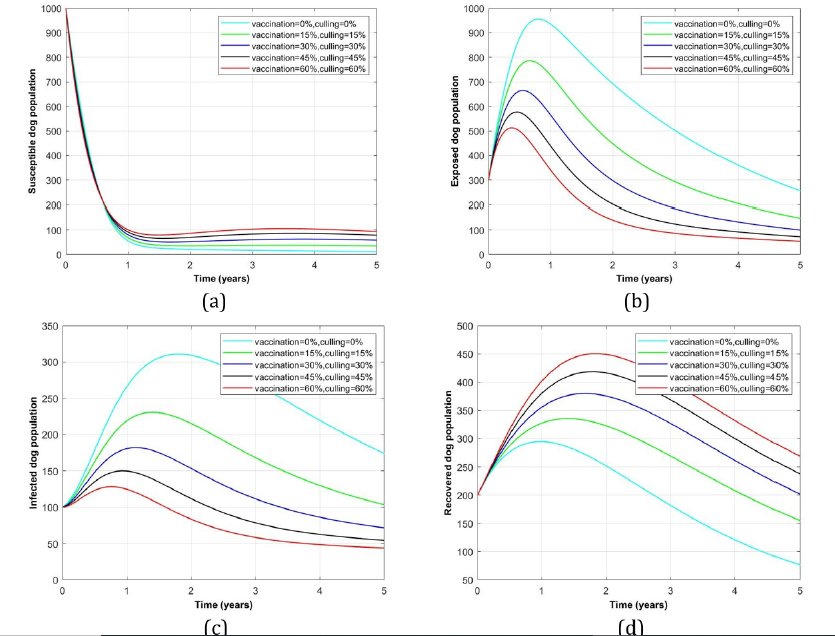
Impact of double interventions of vaccination and culling for rabies disease control in dog population: Figure 6 represents dog population profile in the existence of both vaccination and culling interventions. Panels (a) and (d) indicate decrease and increase of susceptible and recovered dogs as more vaccination and culling rates were increasing respectively. But (b) and (c) representing the exposed and infected dog groups for which as more vaccination and culling rates were administered to both, the more dogs were reduced from their respective classes and vice versa.

Figure 6:Profile of dog population with the variation of both disease interventions, vaccination and culling rates.

In this paper, a model of dog rabies disease infection dynamics involving vaccination and culling interventions is developed to assess the impact of these interventions in clearing dog rabies infections from the dog population. From the findings, it is observed that, in the presence of both interventions the exposed and infected dog population groups (see Figure 3 (a)) were minimum of about 500 and 105 dogs which were surppased by recovered individuals which attained 500 after 2 years respectively. On the other hand, Figure 3 (d) represents its complete absence of both interventions in which the number of recovered dogs approaches zero meanwhile the exposed and infected were increased to the maximum of 940 and 300 digits respectively. However, in the presence of a single intervention considerably vaccination alone (Figure 3 (b)) and culling alone (Figure 3 (c)), the exposed reached the peak of 600 and 700 while the infected number counted 200 and 195 dogs respectively. From numerical results, basic reproduction number, R₀ is found to range between 0.027 ≤ R₀ ≤ 1.258 which implies that for R₀ > 1 it is the absence of double intervention while R₀ < 1 indicates the presence of double interventions in the dog population.

More specifically, it is found that, the combination of both interventions atleast the rate of 60% for vaccination and culling each will be able to minimize the exposed dog group from its peak of 950 to 500 numbers which will be slightly diminishing to less than 100 dogs after 5 years later (see Figure 6 (b)). Similarly, by administering double interventions on the same rate (60%) each, the infected dogs will decrease from its maximum of 310 to 130 and gradually declined to less than 50 dogs after 5 years duration (see Figure 6 (c)). On the other hand, double interventions have a slighly impact on the susceptible dog population provided any intervention rate supplied to them (see Figure 6 (a)), while the recovered dogs were potentially increased more from 300 to 450 numbers for 5 years time as more intervention rates were given to the particular group (see Figure 6(d)).

Therefore, it can be concluded that, dog rabies disease infections can be eliminated from the dog population whenever effective vaccination and culling were practiced in the dog population particularly in the exposed and infectious groups as the most disease carriers and transmitters among the dogs.

Author declares no conflict of interest regarding this work.

Data supporting the work are included in this report.

1. Addo KM (2012) An SEIR Mathematical Model for Dog Rabies. MSc. Dissertation Kwame Nkrumah University of Science and Technology, Bongo District, Ghana.
2. Agaba GO (2014) Modelling of the Spread of Rabies with Pre-Exposure Vaccination of Humans. BN1 9QH, Brighton, United Kingdom 4(8):
3. Asamoah JKK, Oduro FT, Bonyah E, Seidu B (2017) Modelling of rabies transmission dynamics using optimal control analysis. Journal of Applied Mathematics 2017: 1-23.
4. Bilinski AM, Fitzpatrik MC, Rupprecht CE, Paltiel AD, Galvani AP (2016) Optimal frequency of rabies vaccination campaigns in SubSaharan Africa supplemental information. The Royal Society, Proceedings Biological Sciences 283(1842): 20161211.
5. Borse RH, Atkins CY, Gambhir M, Undurraga EA, Blanton JD, et al. (2018) Cost-effectiveness of dog rabies vaccination programs in East Africa. PLoS Neglected Tropical Diseases 12(5): e0006490.
6. Borus P (1996) Rabies: the emergence of a microbial threat. East Afr Med J 73(1): 32-34.
7. Carroll MJ, Singer A, Smith GC, Cowan DP, Massei G (2010) The use of immuno-contraception to improve rabies eradication in urban dog populations. Wildlife Research CSIRO 37: 676-687.
8. Czupryna AM, Brown JS, Bigambo MA, Whelan CJ, Mehta SD, et al. (2016) Ecology and demography of free-roaming domestic dogs in rural villages near Serengeti National Park in Tanzania. PLoS ONE 11(11): e0167092.
9. Driessche PV, Watmough J (2002) Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences 180(1-2): 29-48.
10. Ega TT, Luboobi LS, Kuznetsov D (2015) Modeling the dy-namics of rabies transmission with vaccination and stability analysis. Applied and Computational Mathematics 4(6): 409-419.
11. Esteva PL, Velasco HJX (2002) M-matrices and local stability in epidemic models. Mathematical and Computer Modelling 36(4-5): 491-501.
12. Fitzpatrik MC, Hampson K, Cleaveland S, Mzimbiri I, Lankester F, et al. (2014) Cost-effectiveness of canine vaccination to prevent human rabies in rural Tanzania. Ann Intern Med 160(2): 91-100.
13. Gsell AS, Knobel DL, Kazwala RR, Vounatsou P, Zinsstag J, et al. (2012) Domestic dog demographic structure and dynamics relevant to rabies control planning in urban areas in Africa: The Case of Iringa, Tanzania. BMC Veterinary Research 8(1): 236.
14. Guo C, Li Y, Huai Y, Rao Cy, Lai S, et al. (2018) Exposure history, postexposure prophylaxis use, and clinical characteristics of human rabies cases in China 2006-2012. Scientific Reports 8(1): 17188.
15. Hampson K, Coudeville L, Lembo T, Sambo M, Kieffer A, et al. (2015) Estimating the global burden of endemic canine Rabies. Plos Neglected Tropical Disease 9(5): e0003786.
16. Huang J, Ruan S, Shu Y, Wu X (2018) Modeling the transmission dynamics of rabies for dog, Chinese ferret badger and human interactions in Zhejiang province China. Bull Math Biol 81(4): 939-962.
17. Kamgang JC, Sallet G (2008) Computation of threshold conditions for epidemiological models and global stability of the Disease-Free Equilibrium (DFE). Math Biosci 213(1): 1-12.
18. Kipanyula MJ (2015) Why has canine rabies remained endemic in the Kilosa District of Tanzania? Lessons Learnt and the Way Forward. Infectious Diseases of Poverty 4(1): 52.
19. Kitala PM, McDermott JJ, Coleman PG, Dye C (2002) Comparison of vaccination strategies for the control of dog rabies in Machakos District, Kenya. Epidemiol Infect 129(1): 215-222.
20. Laager M, Lechenne M, Naissengar K, Mindekem R, Oussiguere A, et al. (2019) A metapopulation model of dog rabies transmission in N’Djamena, Chad. Journal of Theoretical Biology 462: 408-417.
21. Li MY (2018) An Introduction to Mathematical Modeling of Infectious Diseases. Mathematics of Planet Earth 2(5): 156.
22. Leung T, Davis SA (2017) Rabies vaccination targets for stray dog populations. Frontiers in Veterinary Science 4: 1-10.
23. Martcheva M (2015) An Introduction to Mathematical Epidemiology. Texts in Applied Mathematics 61(19): 453.
24. Mpolya EA, Lembo T, Lushasi K, Mancy R, Mbunda EM, et al. (2017) Toward elimination of dog-mediated human rabies: Experiences from implementing a large-scale demonstration project in Southern Tanzania. Frontiers In Veterinary Science 4: 21.
25. Mumbu AJ, Hugo AK (2020) Mathematical modelling on COVID-19 transmission impacts with preventive measures: A case study of Tanzania. Journal of Biological Dynamics 14(1): 748-766.
26. Murray RM, Li Z, Stastry SS (1994) A mathematical introduction to robotic manipulation. Taylor And Francis Group, CRC Press, Boca Raton, Florida, USA.
27. Naveed M, Baleanu D, Raza A, Rafiq M, Soori AH, et al. (2021) Modellingthe transmission dynamics of delayed pneumonia-like diseases with asensitivity of parameters. Advances in Difference Equations 468: 1-19.
28. Ndii MZ, Amarti Z, Wiraningsih ED, Supriatna AK (2018) Rabies epidemic model with uncertainty in parameters: Crisp and fuzzy approaches. IOP Conference Series: Materials Science and Engineering 332: 012031.
29. Pieracci EG, Scott TP, Coetzer A, Athman M, Mutembei A, et al. (2017) The formation of the Eastern Africa rabies network: A sub-regional approach to rabies elimination. Trop Med Infect Dis 2(3): 29.
30. Ruan S (2017) Modeling the transmission dynamics and control of rabies in China. Math Biosci 286: 65-93.
31. Safi MA (2019) Global stability analysis of two-stage quarantine-isolation model with holling Type II incidence function. Journal of Mathematics 7(4): 350.
32. Sambo M, Johnson PC, Hotopp K, Changalucha J, Cleaveland S, et al. (2017) Comparing methods of assessing dog rabies vaccination coverage in rural and urban communities in Tanzania. Frontiers in Veterinary Science 4(33): 1-12.
33. Takayama N (2008) Rabies: A preventable but incurable disease. J Infect Chemother 14(1): 8-14.
34. Tian H, Feng Y, Vrancken B, Cazelles B, Tan H, et al. (2018) Transmission dynamics of re-emerging rabies in domestic dogs of rural China. PLoS Pathog 14(12): e1007392.
35. Trawicki MB (2017) Deterministic seirs epidemic model for modeling vital dynamics, vaccination and temporary immunity. Mathematics 5(1): 1-19.
36. Tulu AM, Koya PR (2017) The impact of infective immigrants on the spread of dog rabies. American Journal of Applied Mathematics 5(3): 68-77.
37. Ward JKR, Smith GC, Massei G (2018) Disease transmission mode has little effect on simulated canine rabies elimination. bioRxiv, pp. 1-16.
38. Wiraningsih ED, Widodo AL, Toaha S, Lenhart S (2018) Optimal control for seir rabies model between dogs and human with vaccination effect in dogs. Proceedings of the 6th IMT-GT Conference on Mathematics, Statistics and its Applications (ICMSA2010). Tunku Abdul Rahman University Kampar Campus, Federal Territory of Kuala Lumpur, Malaysia, pp. 1161-1175.
39. World Health Organization WHO (2018) Expert Consultation on Rabies. WHO Technical Report Series, Geneva, Switzerland, p. 1012.
40. Yang W, Lou J (2009) The dynamics of an interactional model of rabies transmitted between human and dogs. Bulletin of the Italian Mathematical Union Series 9 2(3): 591-605.
41. Zhang J, Jin Z, Sun GQ, Zhou T, Ruan S (2011) Analysis of rabies in china: transmission dynamics and control. Plos ONE 6(7): e20891.
42. Zinsstag J, Lechenne M, Laager M, Mindekem R, Naissengar S, et al. (2017) Vaccination of dogs in an African city interrupts rabies transmission and reduces human exposure. Sci Transl Med 9(421): eaaf6984.