- Submissions

Full Text
Approaches in Poultry, Dairy & Veterinary Sciences
Mathematical Analysis of Antibody by Gamma and PSI Functions
Bin Zhao*, Aibing Li and Lichun Liang
College of Science, Northwest A & F University, China
*Corresponding author: Bin Zhao, College of Science, Northwest A&F University, Yangling, Shaanxi, China
Submission: September 13, 2017; Published: December 18, 2017

ISSN : 2576-9162Volume2 Issue2
Abstract
This study aimed to develop mathematical models with important physiological parameters involving immune response for antibody by using Gamma and Psi functions, which could be used in many aspects, for instance to explain the controversies concerning antibody concentration with biological reasons and mathematical calculations, to optimize the antibody yield in large scale production. In this paper, we establish two new logarithmically completely monotonic functions involving the gamma function according to two preferred interaction geometries, necessary and sufficient conditions are presented for one of them to be logarithmically completely monotonic. As a consequence, a sharp inequality involving the gamma function is deduced to solve the problems of genetically engineered antibody. This approach would aid to utilize the engineered antibodies and their derivatives for various biomedical applications.
Keywords: Gamma function; Genetically engineered antibody; Logarithmically completely monotonic; Inequality; PSI function
Introduction
Mathematical or computational models have been proposed in different biological subjects in order to explain various complex phenomena. We have designed this study to monoclonal antibodies and Fc-fusion proteins (Figure 1). At present, it is still difficult to predict the optimal structure of antibodies. Topology knowledge can be important in antibody application as well as transformation. Theoretically, we can obtain desired antibodies by using protein/ gene engineering technology. For instance, we can transform the complementarities determining region (CDR) to promote the affinity of the antibody to antigen. Similarly, we could also transform any domain of antibody to make it bind with any desired target. Under this vision, topology is a powerful tool to predict the structure of protein and it will serve to antibody engineering. Our present work tries to explain, and predict, if possible, the change of structure, size and function of antibodies as well as their fragments from a topological perspective.
Figure 1: Main formats of monoclonal antibodies and Fc-fusion proteins licensed for use in rheumatology.
A. Diagram of infliximab (whole IgG1 molecule against TNFα). Red: VH and VL domains; Blue: constant domains of heavy and light chains. Therapeutic IgGs may differ regarding the heavy-chain isotype and the degree of variable domain humanization. For instance, ixekizumab is a humanized IgG4 and denosumab a fully human IgG2.
B. Etanercept is a fusion protein that combines the TNFα receptor to a human IgG1 Fc fragment. Dark red: cysteine-rich domains (CRD) of the TNFα receptor.
C. Certolizumab pegol is a pegylated Fab fragment. Green: polyethylene glycol chains. Glycosylated proteins (N-glycans and O-glycans) are not shown, to improve readability.
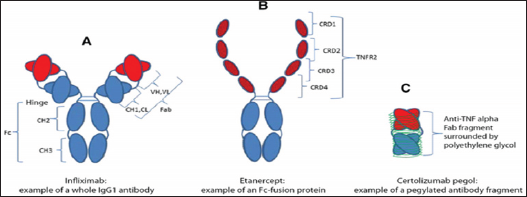
Main formats of monoclonal antibodies and Fc-fusion proteins licensed for use in rheumatology (Figure 1).
a. Diagram of infliximab (whole IgG1 molecule against TNFα ). Red: VH and VL domains; Blue: constant domains of heavy and light chains. Therapeutic IgGs may differ regarding the heavy-chain iso type and the degree of variable domain humanization. For instance, Ixekizumab is a humanized IgG4 and denosumab a fully human IgG2.
b. Etanercept is a fusion protein that combines the TNF α receptor to a human IgG1 Fc fragment. Dark red: cysteine-rich domains (CRD) of the TNFα receptor.
c. Certolizumab pegol is a pegylated Fab fragment. Green: polyethylene glycol chains. Glycosylated proteins (N-glycans and O-glycans) are not shown, to improve readability.
For Re(z) > 0 the classical Euler's gamma function Г and psi (digamma) function Ψ are defined by
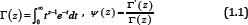
respectively. The derivatives Ψ(n)(z) for n ∈ ℕ are known as polygamma functions. For Ψ(z) [1], the following series representations are established:
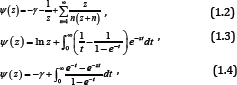
Where, γ = 0.57721566490 --- denotes the Euler’s constant. We next recall [2-5] that a function f is said to be completely monotonic on an interval I, if f has derivatives of all orders on I which alternate successively in sign, that is,
(-1 )nf(n) (x) ≥ 0 , (1.5)
for all x ∈ I and for all n ≥ o . If inequality (1.5) is strict for all x ∈ I and all n ≥ o , then f is said to be strictly completely monotonic. The classical Bernstein-Widder theorem [6], Theorem 12a states that a function f is completely monotonic on (o, ∞) if and only if it is a Laplace transform of some nonnegative measure μ that is,
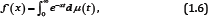
Where, μ(t) is non-decreasing and the integral converges for x > o . We recall also [7-9] that a positive function f is said to be logarithmically completely monotonic on an interval I if f has derivatives of all orders on I and
(-1)n[lnf(x)](n)≥0 , (1.7)
for all x ∈ I and for all n ≥ 1 . If inequality (1.7) is strict for all x ∈ I and all n ≥ 1, then f is said to be strictly logarithmically completely monotonic. The antibody structure will be changed when it binds certain target (Figure 2), i.e.: antigen, receptor. How to describe the changes in the view of topology? The following cases will explain it in detail.
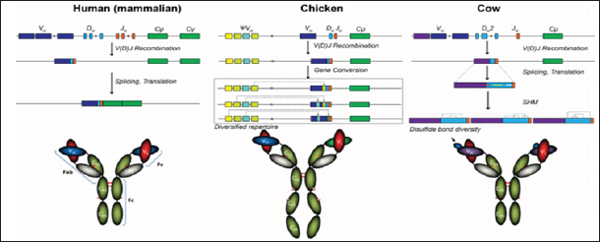
Diagrammatic representation of VH germ-line diversity (top) leading to domain structure diversity (bottom) (Figure 2). In humans, multiple V, D, J regions are rearranged to produce a VDJ segment that encodes the variable region (in this case the VH). The assembled polypeptide is represented by the classically ‘Y’ shaped IgG (150kDa) molecule (bottom), where the various regions of the antibody are labeled and the carbohydrates are indicated by pink dots. Unlike humans or mice, chickens use gene conversion to diversify the antibody repertoire. Single genes encode the VH (and VL) and a single VDJ event, which generates minimal diversity, is preceded by insertion of upstream pseudogenes (WH] in a process that results in donation of diverse sequence fragments into the V region. Chicken antibody (IgY) has a molecular weight of 180 kDa by virtue of an additional constant heavy domain and additional carbohydrate moieties. Cows employ an ultra long CDRH3 repertoire resulting from a VDJ event that utilises a single VH segment (VH Bul), which combines with an elongated D region (DH2) to produce a recombined V-region that undergoes diversification by somatic hyper-mutation. This can introduce or remove cysteine thus, diversifying the disulfide landscape of the repertoire.
Figure 2: Diagrammatic representation of VH germ-line diversity (top) leading to domain structure diversity (bottom).
It was proved explicitly in [8] and other articles that a logarithmically completely monotonic function must be completely monotonic. In [10], G. D. Anderson et al. proved that the function
g (x) = x(ln x-Ψ(x)) (1.8)
is strictly decreasing and strictly convex on (o, ∞) , with two limits
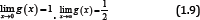
From (1.9) and the monotonicity of g (x), then the double inequalities

holds for all x > o .
In [11], Theorem [1], by using the well-known Binet's formula, H. Alzer generalized the monotonicity and convexity of s (x) , that is, the function
gα(x) = -xα (ln x-Ψ(x)) (1.11)
is strictly completely monotonic on (o, ∞) if and only if α≤1.
In [12], D. Kershaw and A. Laforgia proved that the function 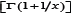 x is decreasing on (o, ∞) and x
x is decreasing on (o, ∞) and x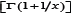 x
is increasing on (0,∞) . These are equivalent to the function
x
is increasing on (0,∞) . These are equivalent to the function 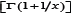 1/xbeing increasing and
1/xbeing increasing and 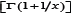 1/x/x being decreasing on (o, ∞) , respectively. In Theorem 5, F Qi & Ch-p Chen [13] generalized these functions. They obtained the fact that for all x > o the function xr
1/x/x being decreasing on (o, ∞) , respectively. In Theorem 5, F Qi & Ch-p Chen [13] generalized these functions. They obtained the fact that for all x > o the function xr 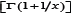 1/x is strictly increasing for r ≥ o and strictly decreasing for r ≤ -1, respectively. After the papain digestion, the remained antibody functional part (usually the Fab domain), will be smaller and the structure is also changed. These changes can be revealed vividly using topology. Recently [14,15], Theorem 1, F Qi, et al. [14] established another excellent result, which states that forgiven y ∈ (-1, ∞) and α ∈ (-∞, ∞), let
1/x is strictly increasing for r ≥ o and strictly decreasing for r ≤ -1, respectively. After the papain digestion, the remained antibody functional part (usually the Fab domain), will be smaller and the structure is also changed. These changes can be revealed vividly using topology. Recently [14,15], Theorem 1, F Qi, et al. [14] established another excellent result, which states that forgiven y ∈ (-1, ∞) and α ∈ (-∞, ∞), let
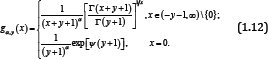
The function (1.12) is logarithmically completely monotonic with respect to x∈(-y-1 ∞) if and only if α≥ max {1,1/ (y +1)}; and if α ≤ min {1,1/2 (y + 1)}, the reciprocal of the function (1.12) is logarithmically completely monotonic with respect to x ∈ (— y — 1,∞) . Antibodies occur spontaneously gathering and forming dimer, polymer, which will influence their functions (Figure 3). In antibody engineering practice, it urgently needs some measures to overcome this difficulty. From topology perspective, we could understand this issue as follow. Stimulated by the above results, we put forward the function as follows: forgiven y ∈ (o, ∞) and real number α, let the function fαy (x) be defined by
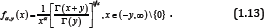
Our First Result is Contained in the Following Theorem
Theorem 1: For the function (1.13), then the following statements are true:
i. For any given y ≥ 1 , the function (1.13) is strictly logarithmically completely monotonic with respect to x∈(— y,∞) \ {o} if and only if α≥ 1;
ii. For any given o <y< l, if α ≥ e-(1-y) Y , then the function (1.13) is strictly logarithmically completely monotonic with respect to x∈(— y,∞) \ {o}
iii. For any given y > o, the reciprocal of the function (1.13) is strictly logarithmically completely monotonic with respect to x∈(— y,∞) \ {o} if and only if α < o .
Our second result is presented in the following theorem.
Theorem 2: For any given y ∈ [1,∞), let the function hy (x) be defined on (o, ∞) by
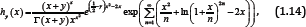
Where, γ denotes the Euler’s constant, then the function (1.14) is strictly logarithmically completely monotonic with respect to x on (o,∞) . The following corollary can be derived from Theorems 2 immediately.
Corollary 1: For any given y ≥ 1, the inequality
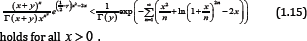
Lemma
In order to prove our main results, we need the following lemmas. It is well known that Bernoulli polynomials Bk (x) and Euler polynomials Ek (x) are defined by

respectively. The Bernoulli numbers Bn are denoted by Bn = Bn (o), while the Euler numbers En are defined by . In [16], the following summation formula is given:

The Bernoulli and Euler numbers and polynomials are generalized [18-21].

Proof: It is obvious that  converges at x = 0. In order to prove (2.16), we need only to show that the inner closed uniform convergence of the series
converges at x = 0. In order to prove (2.16), we need only to show that the inner closed uniform convergence of the series  on (0,∞) . From (2.15), We have
on (0,∞) . From (2.15), We have
 converges, which and
converges, which and
Weierstrass M-test implies that the series 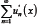 is inner closed uniformly convergent on (0, ∞). Hence, the series
is inner closed uniformly convergent on (0, ∞). Hence, the series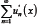 is differentiable on (0, ∞) and the identity (2.17) holds for x ≥ 0 .
is differentiable on (0, ∞) and the identity (2.17) holds for x ≥ 0 .
The lemma is proved.
Lemma5:
For 0 < α ≤ 1 and real number b , let the function Qa,b (x) be defined by

a. Case 1: If O< α≤ 1≤b ,then since q (t) > 0 for t > 0, we have
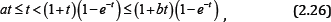
Which, implies αt <(l + bt)(l-e -t), and then p (t )> 0 for all t > 0 .
From (2.24), we know that the inequality (2.20) holds for x ∈(-b/ α, ∞ ) and integer n ≥ 2.

Proof of Theorems
Proof of Theorem 1
For x ≠ 0 and natural number n , taking the logarithmically differential into consideration yields
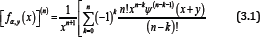
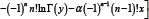
Where, Ψ(—1)(x + y) and Ψ(0)y) and Ψ( x+y) respectively.
Furthermore, differentiating xn+1 [Fαy(x)](n)directly gives
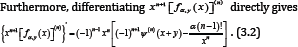
Making use of (2.11) and (2.13) shows that for all n∈ℕ and any fixed y > o, the double inequality

On the other hand, if x∈(0,∞) then the inequalities (3.10) can be equivalently
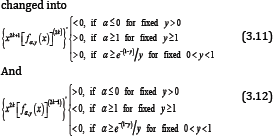

Hence, if either α≥ e-(1-y)/y for given o < y < 1 or α≥ 1 for given y ≥ 1, the function (1.13) is strictly logarithmically completely monotonic with respect to x on (o,⊂), and if α≤o forgiven y>o, so is the reciprocal of the function (1.13).
On the other hand, if x∈(-y,0) for any given y > o, then (3.10) implies
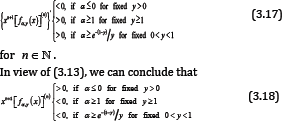
for n ∈ℕ . It is obvious that (3.18) is equivalent to that (3.14) and (3.15) hold for any given y > o and x∈(-y,0). Therefore, it is easy to prove similarly that (3.16) is also valid on x∈(-y,0) for any given y > o and all n ∈ℕ .
Figure 3: Unique Structural Domain in Bovine IgG antibodies and application.

The amino acid of antibody/protein possesses different preferences. Thus we can conduct site-directed mutation to promote the affinity and/or hydrophilic with the prediction of topology. For example, bovine antibodies have an unusual structure comprising a β-strand 'stalk' domain and a disulphide-bonded 'knob' domain in CDR3 (Figure 3). Attempts have been made to utilize such amino acid preference for antibody drug development. Unique Structural Domain in Bovine IgG antibodies and application (Figure 3).
Consequently, the function (1.13) is the same logarithmically completely monotonicity on (-y,0) as on (0,∞), that is, if either α≥e-(1-y)/y for given 0<y<1 or α≥ 1 for given y ≥1 , the function (1.13) is strictly logarithmically completely monotonic with respect to x on (-y,0) , and if α≤0 forgiven y > 0, so is the reciprocal of the function (1.13).
Conversely, we assume that the reciprocal of the function (1.13) is strictly logarithmically completely monotonic on (-y,∞)\{0} for any given y > 0. Then we have for any given y > 0 and all x > 0
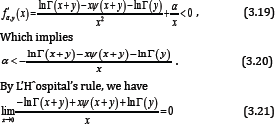
for any given y > 0. By virtue of (3.20) and (3.21), we conclude that the necessary condition for the reciprocal of the function (1.13) to be strictly logarithmically completely monotonic is α≤ 0.
If the function (1.13) is logarithmically completely monotonic on (-y,∞)\ {0} for any given y > 0 , then the inequality (3.19) and (3.20) are reversed for any given y > 0 and all x > 0.
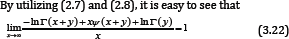
for any given y > 0 . In fact, it is not difficult to show that the necessary condition for the function (1.13) to be strictly logarithmically completely monotonic is α ≥ 1. The proof of Theorem 1 is completed.
Proof of Theorem 2
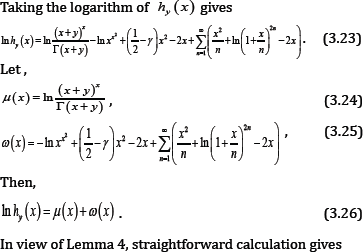
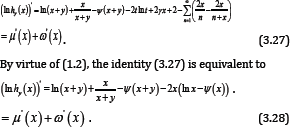
By Lemma 5, we know that μ' (x) is strictly increasing on (0,∞ ), which and (1.10) imply the limit of μ'(x) equals 1 as x →∞, therefore
μ'( x)< 1 (3.29)
holds for all x > 0 .
We know that g (x) is strictly completely monotonic on (0,∞), where g (x) is defined by (1.8), hence for given integer n ≥ 0, the inequality

for all x > 0 . Utilizing Lemma 5 and (3.30), for given integer n ≥ 2, it is easy to see that
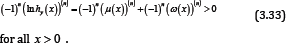
for all x > 0 .
Theorem 2 follows from (3.32) and (3.33). Thus the proof of Theorem 2 is completed [25-31].
Conclusion
In conclusion we establish two new logarithmically completely monotonic functions involving the gamma function according to two preferred interaction geometries, and a sharp inequality involving the gamma function is deduced to solve the problems of genetically engineering antibody. It is necessary to address, many other aspects (such as thermal condition, alkalinity or acidity, adhesion of antibody) are also playing key roles in antibody functioning, which could be also understood from bio-mathematical perspective, and such knowledge will be in return useful for biomedical application of antibodies as well as proteins.
Acknowledgement
This work was supported by the Fundamental Research Funds for the Central Universities (2014YB030), Ministry of Education and State Administration of Foreign Experts Affairs "Overseas Teacher" project (MS2011XBNL057), the Key Construction Pro- gram (2015SD0018) of International Cooperation Base in S&T, Shaanxi Province, China.
References
- Anon (2016) US Broiler Performance.
- Petracci M, Mudalal S, Soglia F, Cavani C (2015) Meat quality in fast- growing broiler chickens. World's Poultry Science Journal 71(2): 363374.
- Song DJ, King AJ (2015) Effects of heat stress on broiler meat quality. World's Poultry Science Journal 71(4): 701-709.
- Sahin K, Smith MO (2016) Regulation of transcription factors by the epigallocatechin-3-gallate in poultry reared under heat stress. World's Poultry Science Journal 72(2): 299-306.
- Kapell DNRG, Hill WG, Neeteson AM, McAdam J, Koerhuis ANM, et al. (2012) Twenty-five years of selection for improved leg health in purebred broiler lines and underlying genetic parameters. Poultry Science 91(12): 3032-3043.
- Honkatukia M, Tuiskula-HM, Ahola V, Uimari P, Schmutz M, et al. (2011) Mapping of QTL affecting incidence of blood and meat inclusions in egg layers BMC Genetics 12: 55.
- Dunn IC (2004) Breeding strategies to improve the egg's natural defense. Worlds Poultry Science Journal 60(4): 458-468.
- Bain MM, MacDade K, Schmutz M, Preisinger R, Waddington D, et al. (2009) The deposition of the cuticle on laying hens eggs is a moderately heritable trait. British Poultry Abstracts 5(1): 17-18.
- Kemps BJ, De Ketelaere B, Bamelis FR, Mertens K, Decuypere EM, et al. (2007) Albumen freshness assessment by combining visible near- infrared transmission and low-resolution proton nuclear magnetic resonance spectroscopy. Poultry Science 86(4): 752-759.
- Lerner IM, Taylor LW, Lowry DC (1951) Selection for increased incidence of blood spots in white leghorns. Poultry Science 30: 748-757.
- Noda K, Nakamura A, Kino K, Kato Y (2007) Genetic improvement by selection for decrease of the meat spots in Nagoya breed. Japanese Journal of Poultry Science 44(1): 17-22.
- Albers G (2010) Genomic selection in poultry and pig breeding - a breakthrough technology? British Poultry Abstracts 6: 13.
- Tuiskula-HM, Honkatukia M, Preisinger R, Schmutz M, de Koning DJ, et al. (2011) Quantitative trait loci affecting eggshell traits in an F(2) population. Animal Genetics 42(3): 293-299.
- Ministry of Agriculture and Cooperatives (2005) Socio-economic impact assessment for the avian influenza crisis: gaps and links between poultry and poverty in smallholders. Department of Livestock Development, Ministry of Agriculture and Cooperatives, The Kingdom of Thailand. (FAO/TCP/RAS/3010e).
- Connolly A (2012) A vision for 2020, the future of poultry. XXIV World's Poultry Congress 5 - 9 August - 2012, Salvador, Bahia, Brazil.
- Leinonen I, Williams AG, Waller AH, Kyriazakis I (2013) Comparing the environmental impact of alternative protein crops in poultry diets: the consequences of uncertainty. Agricultural systems 121: 33-42.
- Leinonen I, Williams AG, Wiseman J, Guy J, Kyriazakis I (2012) Predicting the environmental impact of chicken systems in the UK through a life cycle assessment: broiler production systems. Poultry Science 91(1): 8-25.
- Leinonen I, Williams AG, Wiseman J, Guy J, Kyriazakis I (2012) Predicting the environmental impact of chicken systems in the UK through a life cycle assessment: egg production systems. Poultry Science 91(1): 26-40.
- Vaarst M, Steenfeldt S, Horsted K (2015) Sustainable development perspectives of poultry production. World's Poultry Science Journal 71(4): 609-620.
- Hermansen JE, Horsted K, Kongsted AG (2014) Meat production in organic farming. In: Dikeman M and Devine C (Eds) Encyclopedia of Meat Sciences 2e, 2: 199-203.
- Berardinelli A, Ragni L, Giunchi A, Gradari P, Guarnieri A (2008) Physical- mechanical modifications of eggs for food-processing during storage. Poultry Science 87(10): 2117-2125.
- Cheema MA, Qureshi MA, Havenstein GB (2003) A comprehension of the immune response of a 2001 commercial broiler with a 1957 randombred broiler strain when fed representative 1957 and 2001 broiler diets. Poultry Science 82(10): 1519-1529.
- Dekkers JC (2004) Commercial application of marker - and gene-assisted selection in livestock: Strategies and lessons. Journal of Animal Science 82(E-Suppl): E313-E328.
- Elshire RJ, Glaubitz JC, Sun Q, Poland JA, Kawamoto K, et al. (2011) A Robust, Simple Genotyping-by-Sequencing (GBS) Approach for High Diversity Species. PLoS One 6(5): e19379.
- Elson HA (2015) Poultry welfare in intensive and extensive production systems. World's Poultry Science Journal 71(3): 449-460.
- Havenstein GB, Ferket PR, Qureshi MA (2003) Growth, liveability, and feed conversion of 1957 versus 2001 broilers when fed representative 1957 and 2001 broiler diets. Poultry Science 82(10): 1500-1508.
- Laughlin K (2009) Temperton Fellowship Report No.15, Harper Adams University College, Newport, Shropshire, UK, England.
- Li Y, Willer CJ, Ding J, Scheet P, Abecasis GR (2010) MaCH: using sequence and genotype data to estimate haplotypes and unobserved genotypes. Genetic Epidemiology 34(8): 816-834.
- Nys Y, Bain M, Immerseel, Van F (2011) Improving the safety and quality of eggs and egg products, Cambridge: Woodhead Publishing, Cambridge, UK, pp. 581.
- Van Der Laan MHP (2012) Breeding for genetic resistance to disease. World's Poultry Congress 5 - 9, Salvador, Bahia, Brazil.
- Williams AG, Audsley E, Sandars DL (2009) A Lifecycle Approach to Reducing the Environmental Impacts of Poultry Production. Proceedings and Abstracts, 17th European Symposium on Poultry Nutrition S4.1, p. 7.
© 2017 Bin Zhao, et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






