Non-Classical Cluster Formation in Minerology

The non-classical mechanism of the cluster nucleation is described. This important issue is taken into account in studying a nanocylinder for which, in the simplest model, the thickness of the interfacial layer cannot be determined because it supposedly has a small size. At the same time, it has been shown that the introduction of a special form of anisotropy energy makes it possible to analytically describe the origin of an interfacial layer whose sizes can be regarded. These clusters represent primary mineral particles for which crystallization is one of the possible evolutionary scenarios in mineralogy.

Keywords:Nanocylinder; Cluster nucleation; Surface energy; Anisotropy

The control of the dimensions of the particles and layers of particles in the evolutionary processes is one of the basic problems. These particles and layers of particles represent primary mineral particles for which crystallization is one of the possible evolutionary scenarios in mineralogy. The thermodynamic approach makes it possible to obtain simple relations for the radius of the resulting particle rс [1-5]:

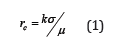
where σ is the specific free surface energy, μ is the change of the chemical potential in the phase transition (i.e., upon nucleation), K is the particle shape factor (for the cylinder K=1). The account for the fact that nucleation may take place on the surface of the macroscopic body (or in the pores) reduces in essence the change of the constants in the equation (1) with account for the phenomenological interaction with the surface of the macroscopic material. The further generalization of the results of the thermodynamic relations to the evaluation of the kinetic phenomena reduces to the introduction of the equilibrium thermodynamic potential (with account for formula (1)) and the use of fluctuation theory. However, in this approach the connection between the thermodynamic concepts and the possible statistical model that is able to include the nucleation phenomenon is not a priori evident. At the present time the computational methods are used for the statistical models, but in this case, it is difficult to generalize the solution and compare it with the general thermodynamic relations. Therefore, the analytic solutions are of interest particularly since – in our view – the solution of a similar problem has already been examined ([6] where the two-dimensional model that is not completely adequate for our problem was examined) is not entirely suitable for the discussion of the physics on the subject phenomenon. Therefore, the first objective of the present work is to derive the analytic expression that is convenient for the discussion – and to draw conclusions relating to the corresponding nucleation problem. We shall show that the division of the total system energy into the free surface energy and the bulk (corn) energy for the phenomenon of the nucleation of the micro- and nano-particles - as was done in [1-6] - is quite arbitrary. This division is easily realized for the systems with induced anisotropy.

The classic Heisenberg statistical model for the two-dimensional space that is applicable for the study of the magnetization of the ferromagnetic material is examined in [6]. It is known that the statistical sum and the thermodynamic functions are determined by the local energy minima. We shall use the variation minimum of the exchange energy (in the cylindrical coordinate system) that was proposed in [2]. As in [6,7], we examine the low- temperature limit, when a single energy minimum is significant. Therefore, we replace the variation of the free energy by the variation of the energy of statistical model

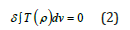
the integration is performed over the entire volume v of particulars, and

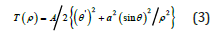
where ρ=r/rс is the radial relative coordinate (0<ρ<1), θ(ρ) is the angle between the cylinder axis and the magnetization vector (π<θ(ρ)<π⁄2),

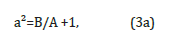
where A is the exchange interaction constant, B is anisotropy coefficient [6,7].

A/2 (θ′)² is the functional responsible for the interaction with near field, also A/2[a²(sin θ)²/ρ²] is the functional responsible for the surface energy. We will examine the nucleation of cylindrical particle. The exchange energy Т(ρ) is the classic analog in the Heisenberg model for the two-dimensional space. Then follows from (2) and from (3) the known nonlinear equation that was presented, specifically, in [6]:

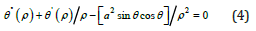
To find the nonhomogeneous equation that physically describes the nucleation process, we specify the corresponding boundary conditions in the form

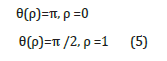
The analogous problem of determining the magnetization of the infinite cylinder was examined previously [2-5], for which was found the analytic relation:

We note that the mathematical solution (6) of the equation (4) was also examined in [6]. This solution is termed the twodimensional soliton (instanton) and is a rare example of the exact analytic solution of the nonlinear problem.

It is possible to obtain the analytic solution which corresponds only qualitatively to the real situation. We see that the obtained solution does not make it possible to clearly divide the system energy into the surface energy and the corn energy. We can consider that this conclusion will remain valid with the increase of temperature. Consequently, the simplified model corresponds to the real physical problem. We shall examine the general case that corresponds to the exactly solvable model. This case makes it possible to find the criterion that determines when the expression (1) can be used adequately. We should present calculation of change of the angle θ from the beginning of coordinates (when ρ =0) a cylindrical particle up to its surface (when ρ =1).

If a=1, there is no anisotropy in the system, and if a>1, the external anisotropy exceeds the exchange interaction in the system. To compare the results for the two cases, we present the calculated variation of the angle θ from the coordinate origin (where ρ=0) of the cylindrical particle to its surface (where ρ=1) (Figure 1). At the same time (Figure 1) let us limit our examination to the two extreme cases of the value of the parameter a:

Figure 1:Function θ(ρ) is the angle of an inclination to an axis of the cylinder (which characterizes energy of a particle in Heisenberg model from the given radius ρ coordinates of a particle).

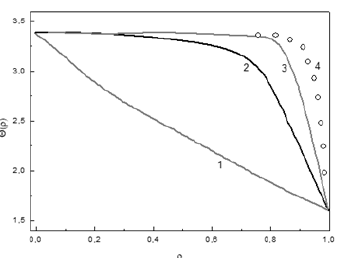
a. curve 1 corresponds to the case a=1, which relates to the condition when microscopic anisotropy is absent,
b. curve 2 corresponds to the case a=10, which refers to the condition when microscopic anisotropy exists,
c. curve 2 corresponds to the case a=50,
d. curve 2 corresponds to the case a=100.

It is shown that, in the first case, it is difficult to isolate the volume of the cylinder that can be attributed to the surface energy, since the angle θ changes smoothly as a function of ρ. In the second case, when a=10, a range can be chosen whose volume amounts to the surface energy of the cylindrical particle. In the framework of our qualitative examination, we may conventionally assume, for example, that the surface layer is counted from the value ρ~0.8. We make this choice using only the shape of curve 2, which sharply decreases for ρ>0.8. The volume that defines the surface energy of the cylinder amounts to 30% of the cylinder’s volume in this case. When an increase further (for example, by a factor of a=100), this volume will amount to less than 10% of the cylinder’s volume.

With decrease the particles the thermodynamic state of its surface will play an ever-increasing role in describing its thermodynamic state. This article presents a very simple model that shows it becomes more and more difficult to separate the thermodynamic functions into the corn and surface functions. The physical consequence of the examined model reduced to the fact that this separation into the corn energy and the surface energy can be performed if the anisotropy in the system significantly exceeds the close-order isotropic exchange interaction. We end with an outlook on future mineralogy’s work.

1. Ono S, Kondo S (1960) Molecular theory of surface tension in liquids. Structure of Liquids. Series Encyclopedia of Physics, Springer, Berlin, Heidelberg, 3(10): 134-280.
2. Rowlinson JS, Widom B (1989) Molecular theory of capillarity. Oxford University Press, Oxford, USA.
3. Jaycock MJ, Parfitt GD (1981) Chemistry of interfaces. Halstead Press, John Wiley & Sons, New York, US.
4. Adamson AW, Gast AP (1997) Physical chemistry of surfaces. Wiley-Interscience Publication, John Wiley & Sons, New York, US.
5. Rusanov AI, Prokhorov VA (1996) Interfacial tensiometry. Elsevier, Amsterdam, Netherlands.
6. Laroze D, Baranov SA, Vargas P, Vazquez M (2007) On the theory of nucleation in cylindrical magnetic nanoparticles. Phys Stat Sol 4(11): 4170-4173.
7. Baranov SA (2021) Modeling of micro-and nanocylinder. J Anal Tech Res 3(2): 28-38.