The Comparative Review of Wave Properties of Finite and Infinite Periodic Crack Arrays

In the present paper we continue to study the properties of metamaterials with application to mechanical, electromagnetic, and acoustic problems possessing some specific periodic internal structure [1]. The most part of the theoretical methods are based on numerical treatment such as Boundary element method and also some semi-analytical methods actively used for infinite or semi-infinite periodic structures, which are based on some asymptotic (low-frequency or high-frequency) estimates, being valid only in the far zone of the wave field [2,3]. In [4], the analytical formulas for the coefficients of reflection and transmission in the low frequency range of the acoustic, electromagnetic and elastic waves, penetrating through the periodic system of holes of arbitrary shape and three-dimensional obstacles, are presented. Two-dimensional problems of wave propagation through a periodic screen lattice in elastic bodies with a single-periodic system of cracks are studied in [5,6] and a doubly-periodic system is considered in [7,8]. In [9] the problems of diffraction by a plane lattice of cylindrical cavities are solved. The wave properties of elastic media containing periodic structures of more complex physical nature–pores, inclusions, and etc. have been analyzed in [10,11]. The problems discussed in this paper are related to the theory of the so-called “acoustic metamaterials”, which, due to their specific internal structure, have the properties of acoustic filters. It means that such a material is able to pass the wave over certain frequency intervals and lock the wave channel for other frequencies. The property was experimentally discovered and presented in [12]. Some fundamental aspects related to the acoustic metamaterials are discussed in [13] and some other publications.

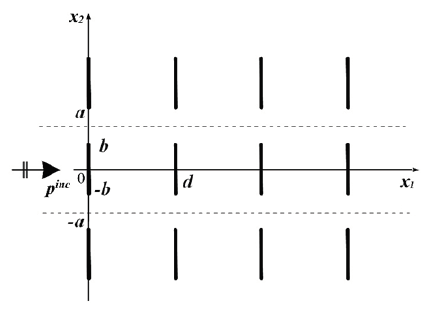
To study the filtration properties of the metamaterials, the normal incidence of a plane longitudinal wave, propagating in an unbounded medium p^inc= e^ik₁x₁ on a doubly-periodic system of finite number of identical vertical arrays, which are finite or infinite along x₂ and finite in the direction x₁ , is considered. Each of them is an ordinary periodic system of coplanar linear cracks located at x₁ = 0,d,2d,.... (M−1) d,M (>2). In the infinite case, under the natural symmetry, the problem is reduced to the consideration of a plane waveguide of the width 2a, which includes M cracks (Figure 1). For the finite case it is necessary to solve the corresponding boundary integral equation over all available contours of the crack system. It is assumed, that with the normal wave incidence e^{i(k₁x₁−ωt)} there is a regime of one-mode propagation at k₁a < π , where k₁-the wave number of the longitudinal wave, 2a-the period of the system in the vertical direction, d-in the horizontal one. The semi-analytical method is used when the distance between the adjacent parallel arrays d and the incident wavelength λ = 2π/k are such that the condition λ/ d >> 1 is satisfied. A comparative analysis of the properties of the scattering parameters is carried out for the three diffraction problems for a finite and infinite periodic system in a scalar formulation, as well as for an infinite periodic system under the conditions of the plane problem of the elasticity theory. The solution of the three diffraction problems was carried out in [2,5]. Let us cite here only the main properties of the periodic systems for the numerical comparative analysis.

Figure 1: Incidence of a plane wave on a periodic array of linear obstacles.

Let us perform a numerical analysis of the problems for the medium with the longitudinal wave speed c₁=6000m/s (steel) when the ratio of the longitudinal and the transverse wave speeds is c₁/ c₂=1.87. Let us compare the moduli of reflection coefficients versus frequency parameter between the three studied cases for a single vertical array, M=1 (Figure 2) and when there are two vertical rows, M=2 (Figure 3), where line 1 means infinite array, elastic theory; line 2-infinite array, scalar theory; line 3-finite array with M₁=7 vertical cracks, scalar theory. We assume, that the longitudinal wave speed in the plane elastic problem is equal to the transverse wave speed for both scalar problems. This condition shortens the one-mode frequency interval of the values ak, whose limit becomes equal to π /1.87 = 1.680 (Figures 2 & 3). In Figures 4 & 5 the comparative analysis of the scalar problems has been performed for the transverse incident wave. For all cases the filtration interval can be seen in the upper part of the one-mode frequency range. It is shown that lines 2 and 3 in Figures 2 & 3, related to the scalar problems, are practically coinciding that takes place even for N=10 cracks in each vertical array. It should be noted that line 1 related to the elastic problem, shows a significant domination of the filtration property, when compared with both infinite and finite scalar problems. Thus, for two vertical arrays in the elastic problem a perfect filtration takes place for ak ≥ 0.7 , but for one vertical row this property is valid only for ak ≥ 1.5 . This also confirms the evident property, that with the growth of the vertical rows the filtration becomes stronger. Let us pass to the analysis of the grid size to the precision of the obtained results. It is stated in [5], that in the case of a single obstacle it is sufficient to take 10 grid nodes per each wavelength, to provide reliable results. Thus, for the frequency 0.16MHz in this formulation the wavelength is 0.0375m, hence on the obstacle of the length 0.015m it is sufficient to take only 5 nodes.

Figure 2:Comparison of three different periodic models: one vertical row (M=1), period of the lattice is 0.02m, size of each crack is 2b=0.015m.

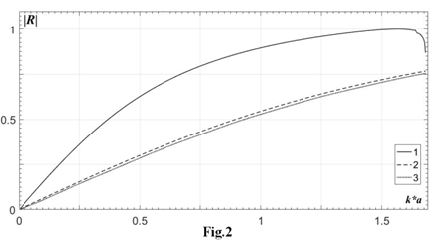
Figure 3: Comparison of three different periodic models: two vertical rows (M=2), period of the lattice is 0.02m, size of each crack is 2b=0.015m, distance between the rows is d=0.02m.

However, the complex geometry of the diffraction lattice requires greater number of nodes. It can be seen from (Figure 4), which represents the results for the array of 10 vertical rows (M=10), each containing 10 obstacles (M₁=10), that with 10 nodes (n=10) over each obstacle the calculations are correct only in the low-frequency case (for ka<1). The analysis shows, that for 5 vertical arrays (M=5) with the obstacles of the length 1.8cm, 10 obstacles in each vertical row (M₁=10) are sufficient to get finite case quite close to the infinite one (Figure 5). It is stated that with the growing number of obstacles in a single vertical row, so with the growth of the parameter M₁, keeping all other parameters unchanged, the interval of the frequency cutoff varies insignificantly. The reflection inside this frequency interval is almost constant, being equal to unit value. This property takes place also for infinite arrays, where M₁ is a number of such arrays.

Figure 4: Comparison of two scalar models: ten vertical rows (M=10), period of the lattice is 0.02m, size of each crack is 2b=0.015m, distance between the rows is d=0.02m; problem 1-infinite array; problem 3-finite array with M1=10 vertical cracks; n is the number of the numerical grid nodes on each crack.

Figure 5: Comparison of two scalar models: five vertical rows (M=5), period of the lattice is 0.02m, size of each crack is 2b=0.018m, distance between the rows is d=0.02m; problem 1-infinite array; problem 3-finite array with various number of M1 vertical cracks.

a. Virtually any frequency interval with the wave channel locking can be created by controlling the relative crack size, the number of vertical arrays and the lattice period in the horizontal direction.
b. When the number of cracks in one row increases, the locking interval changes slightly. And the analysis shows that even 10 cracks sufficiently well approximate the case of the infinite system.
c. The properties of the problems in the scalar formulation [1,3] demonstrate the possible replacement of infinite crack arrays by the finite periodic systems while maintaining the filtration properties.
d. The enhancement of the locking property of the wave channel occurs when considering infinite doubly- periodic systems in the context of the elastic model in comparison with the infinite and finite scalar analogue.

The reported study was supported by the Russian Science Foundation (RSCF), according to the research Project No. 15-19- 10008-P.

1. Deymier PA (2013) Acoustic metamaterials and phononic crystals. Springer-Verlag Berlin, Heidelberg, Germany.
2. Scarpetta E (2002) In plane problem for wave propagation through elastic solids with a periodic array of cracks. Acta Mechanica 154: 179-187.
3. Sumbatyan MA, Remizov MY (2017) On 3D theory of acoustic metamaterials with a triple-periodic system of interior obstacles. Advanced Struct Materials 41: 19-33.
4. Zarrillo G, Aguiar K (1987) Closed-form low frequency solutions for electro-magnetic waves through a frequency selective surface. IEEE Trans Anten Prop AP-35: 1406-1417.
5. Popuzin VV, Remizov MY, Sumbatyan MA, Brigante MA (2019) Comparative analysis of wave properties of finite and infinite cascading arrays of cracks, Springer series: Advanced Structured Materials 109: 97- 112.
6. Angel YC, Bolshakov A (2000) In-plane waves in an elastic solid containing a cracked slab region. Wave Motion 31(4): 297-315.
7. Mykhaskiv VV, Zhbadynskyi IY, Zhang C (2014) Dynamic stresses due to time-harmonic elastic wave incidence on doubly periodic array of penny-shaped cracks. J Math Sci 203: 114-122.
8. Remizov MY, Sumbatyan MA (2018) 3-D one-mode penetration of elastic waves through a doubly periodic array of cracks. Math Mech Solids 23(4): 636-650.
9. Popuzin VV, Zotov VM, Sumbatyan MA (2017) Theoretical and experimental study of an acoustically active material containing a doubly-periodic system of cylindrical holes. Advanced Materials, pp. 293-308.
10. Datta SK (1977) Diffraction of plane elastic waves by ellipsoidal inclusions. J Acoust Soc America 61(6): 1432-1437.
11. Yang Ch, Achenbach JD (2017) Time domain scattering of elastic waves by a cavity, represented by radiation from equivalent body forces. Int J Eng Sci 115: 43-50.
12. Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, et al. (2000) Locally resonant sonic material. Science 289(5485): 1734-1736.
13. Craster RV, Guenneau S (2013) Acoustic Metamaterials. Springer Series in Materials Science, Germany.