Thermodynamics of the Solid Solutions of Isomorphic Substances

Introduction

The study of the conditions and characteristics of the formation of solid solution play an important role in research the processes of formation of mineral and the technology of processing mineral raw materials. The thermodynamics characteristics of the formation of binary solid solutions of isomorphic substances can be calculated using the classical expression for the crystal lattice energy associated with determination of the Coulomb potential and repulse potential in a form acceptable for both components. At the same time this problem can be solved in a more convenient way, using general relations characterizing the dependence of thermodynamics functions on the volume of the system, which leads to an adequate description of the experimental data.

Theory

Let us consider binary solid solutions of substitution when an impurity component is embedded in the crystal lattice of the main component without the formation of defects. In addition, we use the so-called quasi-harmonic approximation where it is assumed that the vibrations of atoms around the middle equilibrium positions correspond to vibrations of simple harmonic oscillators and the potential energy has a minimum value in these positions. Quantum theory says that the possible levels of the oscillator are defined as

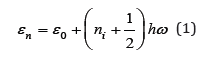
where ε0 is the potential energy in equilibrium, h is the Plank constant, ω is the vibrational frequency and ni are integers from zero to infinity. Summing Eq.(1) over all states from the lowest vibrational level at ni=0, we can determine the partition function [1]

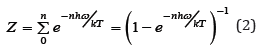
where T is a temperature and k is the Boltzmann constant (hω/k is the Einstein temperature). The total free Helmholtz crystal energy for 3νN oscillators, where N is the number of atoms and ν is a stoichiometric coefficient, can be determined as

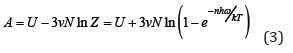
where 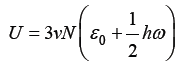the energy of the fundamental quantum state, which includes the energy of zero vibrations of atoms 1/2 hω. At high temperatures we can expansion of the expression

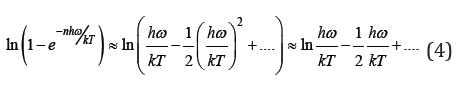
and convert Eq.(3) to the form of classical energy

where U₀ = 3vNε₀ is the potential energy when all atoms are in equilibrium. Differentiating Eq. (5), we can determine the pressure

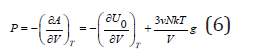
where V is the volume of system and g is the Gruneisen constant is the same for all normal vibrations [2]

Eq.(7) shows that the vibrational frequency varies depending on the volume as

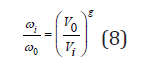
where ω_i is the frequency when the volume is V_i and ω₀ is the frequency when the volume is V₀. The volume of a solid solution, according Retgers rule, can be represented as

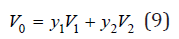
where y₁, y₂ are the mole fractions of the components (y₁+y₂=1) and V₁, V₂ are the volumes of pure components having the common atom in its structures. When a common atom is surrounded by atoms of various species, this atom is shifted towards the atom having a high charge density. It leads to a local change in volume [3]

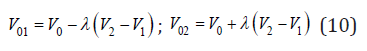
where λ is the value characterizing the displacement of atoms from ideal crystallographic positions in solid solution, subject to equality 1/2 (v₀₁+v₀₂)-v₀.

Differentiating Eq.(5), we can determine the entropy of system

The change in entropy during the formation of a solid solution associated with a change in the vibrational frequencies of the atoms can be defined as

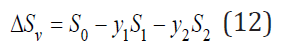
where the subscript “1”, “2” and “0” refer to pure components and the solid solution, respectively. Substitution Eq.(11) into Eq.(12), we have

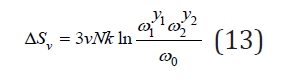
Given the different configurations of the surrounding of the common atom by d ifferent or identical species of atoms, for example, halogen atoms around the potassium atom in a solid solution KCl- KBr, the average vibrational frequency can be represented in the form

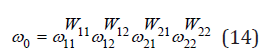
where ω_ii, ω_ij are the frequencies corresponding to the surrounding of the common atom by identical and different species of atoms and W_ii, W_ij are probabilities of these combinations

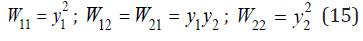
The mechanical theory of vibrations shows that in discrete systems waves with a frequency exceeding a certain final value cannot propagate. For a selected pair of atoms this value can be determined as [2]

where C is the force constant and M is the reduced mass of atoms. Using Eq.(16), the vibrational frequencies for various configurations can be expressed as

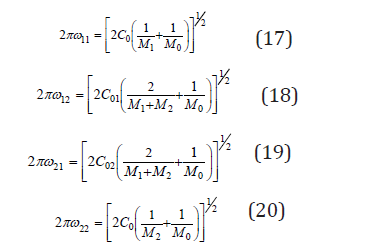
where M₁ , M₂ are the masses of replaced atoms and M₀ is the mass of common atom (or a group of atoms for complex compounds). For each of the individual components, we can also write

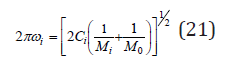
Combining Eq.(8) and Eq.(16), we can determine the ratio

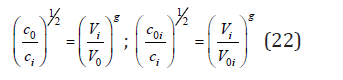
Then, using Eq.(17)-(22), the average frequency of atomic vibration in a solid solution according Eq.(14) can be determined as [3]

where

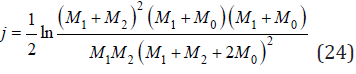
and

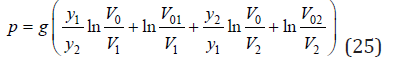
Using Eq.(9), (10) and expansion ln (1+ x) = x , we hav

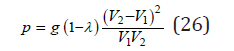
Here, as a first approximation, we can put λ=1/2 , whence

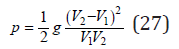
Substitution Eq.(23) into Eq.(13), we have

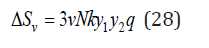
where q = j + p .
A complete change of entropy during solid solution formation can be defined as

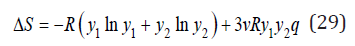
where the first term is the entropy of ideal mixing Sid and R is the gas constant R=Nk , where N is the Avogadro number.

At high temperature (here we consider an approximation where the remaining terms of expansion (4) can be neglected) the total energy of a solid can be determined according to Eq.(5) and Eq.(11) as

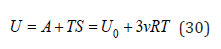
where the last term is the same for both the solid solution and the components forming it, so the change in energy during the formation of a solid solution can be represented as

where the functional dependence of energy on volume is emphasized. Function U₀(V₀) can be represented as a hybrid function of the original components [3]

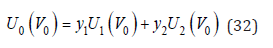
Take into account the probabilities of various configurations, Eq.(32) should be written as

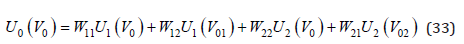
where V₀₁ and V₀₂ are defined by Eq.(10). Substituting Eq.(33) into Eq.(31), we have

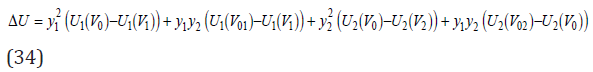
The functions U_i (V₀) and U_i (V_0i) for each of the components can be expanded into Taylor series keeping only the quadratic terms in it, since dU/dV=0 in equilibrium. Then, using Eq.(9), we can write, for example, for the first component

where

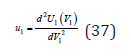
Similar expressions when replacing subscripts can be written for another component. Further, combining Eq.(34)-(36), we have

Using the condition of minimum energy 0 d U dλ Δ = , we have

Substituting Eq.(39) into Eq.(38), we obtain

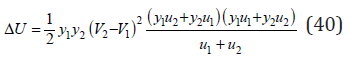
Turning to a change in enthalpy according to Eq.(6), we have

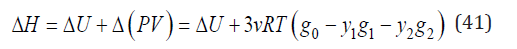
For isomorphic substances, which have a similar properties, the last term of Eq.(41) can be neglected, therefore, we can put ΔH=ΔU. Than the Eq.(40) can be transformed to the form [3]

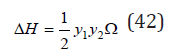
where the value of 𝛺 can be determined in good approximation as

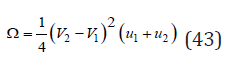
Finally, the change of Gibbs energy during the formation of a solid solution, according Eq.(29) and (42), can be represented as

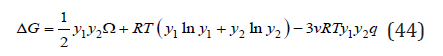
Further using condition dΔG/(dyi )=0, we can determine the critical temperature of the decomposition of the solid solution

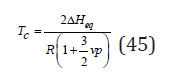
where ΔH_eq corresponds to the equal molar ratio of components.

Discussion

One of the main controversial issues in the theory of the formation of inorganic solid solution is the existence of ordered structures [4,5]. To solve this problem, we consider a partially ordered solution, where probabilities of surrounding a common atom with the same and different atoms can be represented as [4]

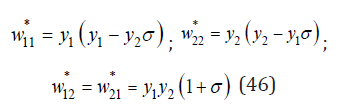
where σ is a degree of local order. Then the entropy of mixing can be defined as

and Eq.(30) can be transformed to

By transformations similar to Eq.(31)-(34) , the change enthalpy during the formation of a solid solution can be expressed as

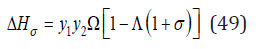
where

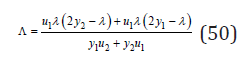
Using the condition of minimum Gibbs energy dΔG/dσ=0, we have [6]

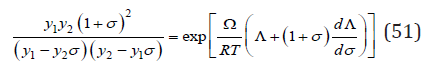
Further, to simplify the view of formulas, we consider, without loss of generality, a solid solution with an equal molar ratio of components. Then the solution of differential equation (51) can be represented as

The integration constant Λ0 can be determined from the boundary condition – for σ=0 and λ=1/2 , according to Eq.(50), we have Λ0=1/2 . Substituting Eq.(52) into Eq.(49) and to make a comparison with Eq.(42), the change enthalpy when ordering the solution can be determined as

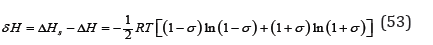
The change in entropy under these conditions can be defined as S Sσ Sid δ = − and using Eq.(47) to determine the change in Gibbs energy as δ G = δ H − Tδ S = 0 . Thus, the coupling Eq.(52) provides a minimum Gibbs energy for any conjugate values of 𝜆 and 𝜎. The most convenient calculation is at σ=0 using Eq.(44). Note that in this case entropy takes the maximum value.

For practical calculations, we define ui as

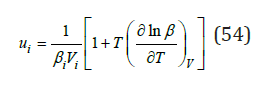
where 𝛽 is the compressibility and the last term is about 5-10% of the basic value [3]. Thus, the value of V, 𝛽 and g for a pure components are required to calculate all thermodynamics characteristics of the formation of solid solutions. This data and calculation results according Eq.(42) are given in Table 1 & 2. Figure 1 shows that the change in enthalpy during the formation of a solid solution is close to a symmetric parabolic shape.

Figure 1: Enthalpy of formation of solid solutions. Calculated curve and experimental dots [7]. 1: NaCl-NaBr, 2: KBr-KI, 3: NaBr-NaI, 4: NaBr-KBr.

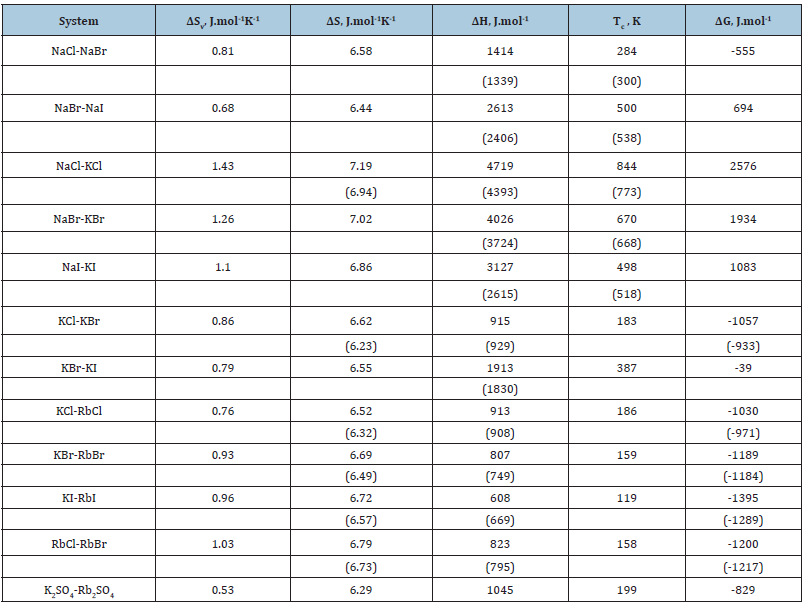
Table 1: The properties of the individual components at 298K [3].

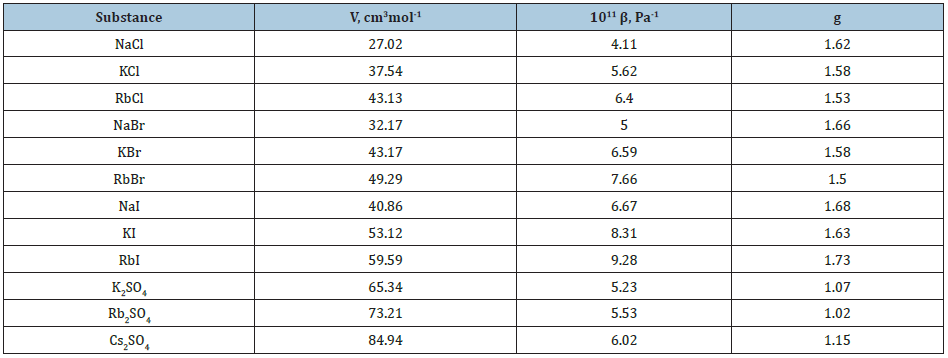
Table 2: Thermodynamics data of solid solutions of equal molar composition at 298K. In parentheses are experimental values, Ref. [3].

Using Eq.(44),we can define the excess mixing energy

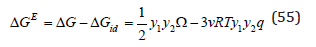
and further, using well-known ratio, the chemical potential of the component (Gibbs partial energy), for example, with a subscript “2”

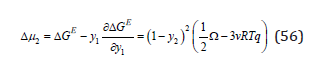
This value determines the difference in the chemical potential of the component in a real and ideal solid solution, from where the activity coefficient of the component can be determined as

where

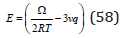
Such solutions can be called quasi-regular, their difference from regular solutions consist in taking into account the vibrational component of entropy.

Co-crystallization coefficient of any component, for example, with subscript “2”, can be represented as [8]

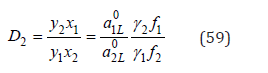
where x₁ and x₂ are relative concentrations of components of mixed liquid solution (x=νm/W , m is molality, W is number of moles of solvent per 1kg), γ₁ and γ₂ are activity coefficients, 0 a1L and 0 a2L are activity of components of saturated binary solutions, In differential form Eq.(59) can be written as

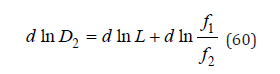
where

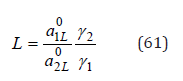
The activity coefficient of component in a mixed solution, according Ref. [8], can be represented as

where ai* is the activity of component in an isopiestic binary solution. Using Eq.(61), (62) and the boundary conditions, we can determine the derivative function ln L d dy as the change in value ln L in the range of concentrations from y2=0 to y2=1 :

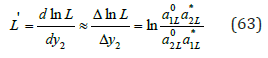
where aiL* is the activity of a component in its binary solution, which is isopiestic to the saturated solution of another component. Using Gibbs-Duhem equation for solid phase

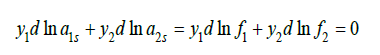
where ais = yi fi is activity of component in solid phase, and Eq.(57), we have

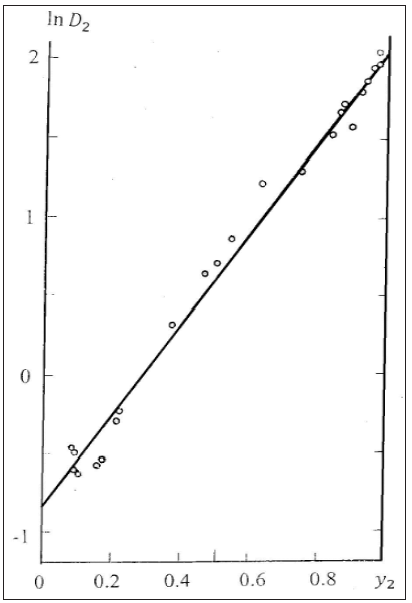
Substituting Eq.(63) and (64) into Eq.(60), we obtain to linear dependence of the co-crystallization coefficient from composition (Figure 2)

Figure 2: Co-crystallization coefficient in the system Rb₂SO₄-K₂SO₄-H₂O. Calculated line and experimental dots [9].

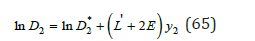
For other component, we can use definition ln D1 = − ln D2 . Thus, according Eq.(65), the co-crystallization coefficient can be defined for any ratio of components, whence it follows that the minimum value of the co-crystallization coefficient D2* takes in the limiting case when y2 → 0 . In this method the values ai* can be determined by comparing the osmotic coefficients in binary solutions of both components, using extrapolation of data for one of components to the field of supersaturated solutions [10,11]. Therefore, as a first approximation it is possible to apply a simpler method of calculation of co-crystallization coefficients using the ratio 1 2 1 γ γ ≈ for a mixed solutions, which is confirmed for compounds with similar properties [12]. Then, using Eq.(57) and (59), we have

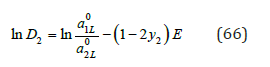
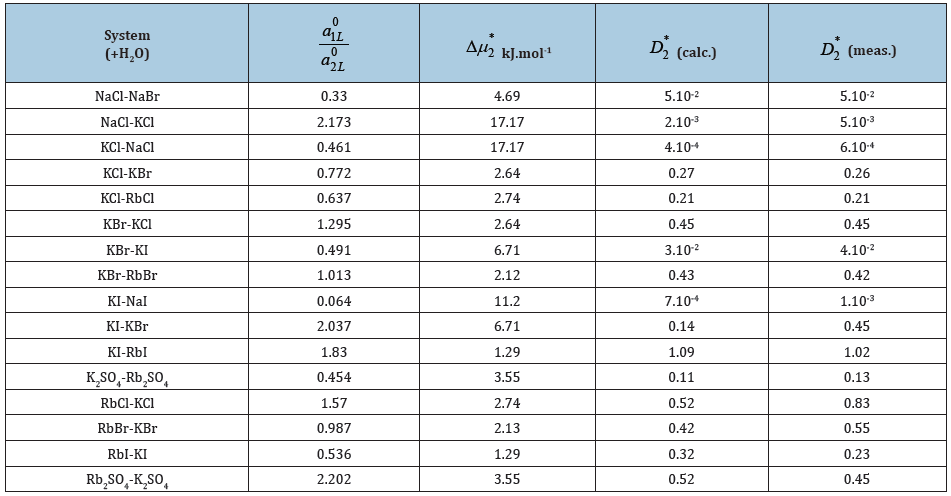
The results of calculation according to Eq.(66) show its acceptability for the estimation of co-crystallization coefficient (Table 3); [13].

Table 3: Co-crystallization coefficient in ternary water-salt systems at 298K. Experimental data D2* from Ref. [13]. Impurity component is the second in writing.

Conclusion

The considered model of the formation of solid solutions allow to determine the thermodynamics parameters of solutions based on the properties of the individual components of solution. This model is also applicable for calculating co-crystallization coefficient in the entire composition range of ternary water-salt systems, including the area of micro-concentration of the impurity component where the co-crystallization coefficient takes a minimum value.

References

1. Landay LD, Lifshits EM (1995) Statistical physics. Moscow, Russia.
2. Girifalco LA (1973) Statistical physics of materials. NY J Wiley & Sons, New York, USA.
3. Allakhverdov GR (2019) Thermodynamics of solutions and separation of elements during crystallization. Moscow, Russia.
4. Wasastjerna JA (1949) On the theory of the heat formation of solid solutions. Soc Sci Fenn Comm Phys Math 15(3): 13.
5. Hietala J (1963) Heat of formation of the sodium chloride type. Annal Acad Sci Fenn 122: 32.
6. Allakhverdov GR (1980) Thermodynamics of formation of the solid solution. Zh Phys Chem 54(3): 617-621.
7. Lister MW, Meyers NF (1958) Heat of formation of some solid solutions of alkali halides. J Phys Chem 62(2): 145-150.
8. Allakhverdov GR, Zhdanovich OA (2019) Theoretical aspects of obtaining pure inorganic substances during crystallization from solutions. AMMS 3(2): 396-397.
9. Stepin BD, Allakhverdov GR (1976) Thermodynamics of system K₂SO₄-Rb₂SO₄-H₂O at 298K. Zh Inorg Chem 21(11): 311-315.
10. Allakhverdov GR, Zhdanovich OA (2019) Thermodynamics of the ternary water-salt systems. AMMS 4(3): 491-494.
11. Allakhverdov GR (2019) Thermodynamics of the electrolyte solutions. AMMS 4(1): 465-474.
12. Ratner AG, Makarov LL (1960) Thermodynamics of system KCl-RbCl-H₂O at 298K. Zh Phys Chem 34(11): 2495-2501.
13. Allakhverdov GR, Mikhlin AL (2017) Separation factor for the crystallization of inorganic substances from aqueous solutions. Inorganic Materials 53(5): 525-528.