- Submissions

Full Text
Aspects in Mining & Mineral Science
Calculation of the Density of Electrolyte Solution
Allakhverdov GR* and Zhdanovich OA
1State Scientific Research Institute of Chemical Reagents and High Purity Chemical Substances- National Research Centre Kurchatov’s Institute, Russia
*Corresponding author: GR Allakhverdov, State Scientific Research Institute of Chemical Reagents and High Purity Chemical Substances-National Research Centre Kurchatov’s Institute, Russia
Submission: August 12, 2019;Published: September 04, 2019

ISSN 2578-0255Volume3 Issue3
Abstract
Based on the solvate model of solutions, the relation of density with the thermodynamics functions is established and an equation for the density of binary solutions is obtained. A generalization of this equation to mixed electrolyte solutions is given.
Keywords: Partial molar volume; Activity of solvent; Hydration number
Introduction
The density of electrolyte solutions plays a large role in the processing mineral row materials, since in many cases it is the main source of information of the concentration of substances in solutions. The exact equation for the density of solutions is also of great theoretical importance for determining the partial molar volumes of electrolytes and the osmotic pressure of solutions. This article proposes a method for describing the density of binary and mixed solutions on the solvate model of solutions.
Theory
Let us consider a binary solution containing m moles of electrolyte and w mole solvent (e.g. water) in the volume of solution V. If we assume, without loss of generality, that positive and negative ions form hydrated complexes of a fixed composition containing np and nn solvent molecules, respectively. than the volume of such solution can be determine as
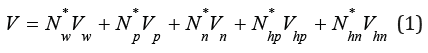
where Nw *, Np *, Nn *, Nhp *, Nhn * are equilibrium amounts of solvent, ions and hydrated complexes, Vw is molar volume of pure solvent, Vp, Vn, Vhp, Vhn are molar volumes of ions and hydrated complexes, respectively. Taking into account the equations of material balance
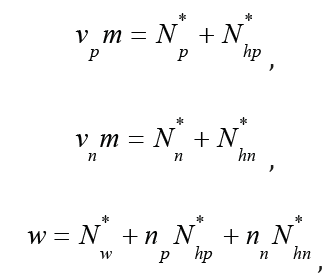
Eq.(1) can be represented in the form
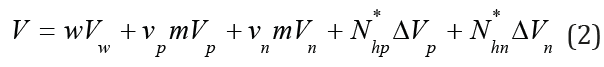
where νp and νn are the stoichiometric coefficients (ν=νp+νn is stoichiometric coefficient of electrolyte), ΔVp = Vp + hp Vw −Vhp, ΔVn = Vn + hn Vw −Vhn . Here the hydration number of corresponding current concentration of each ions hp, hn can be defined as
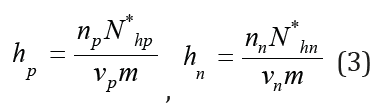
These values according to Ref.[1] can be expressed in the form
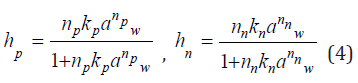
where Kp and Kn is constant of formation of hydrated complex, aw is the activity of solvent.
Using Eq. (3), Eq. (2) can be transformed to

Differentiating Eq. (5), we can determine the partial molar volume of the electrolyte, which in the infinitely dilute solution takes on the value
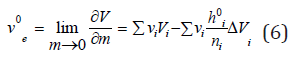
Combining Eq. (5) and Eq. (6), we have
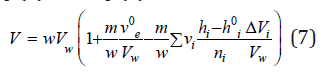
where hi0 is the hydration number of ions in the infinitely dilute solution, which can be determined from Eq. (4) at aw⤑1. The density of the solution is determined by the formula
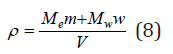
where Me and Mw are molecular weights of the electrolyte and solvent, respectively. Mass fraction of electrolyte in solution z can be defined as
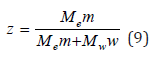
hence the equality

Substituting Eq. (10) into Eq. (7) and then the result obtained into Eq. (8), the latter can be expressed as
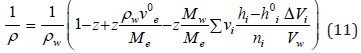
where ρw is the density of pure solvent. Let us further imagine the hydration number of the electrolyte hi as a function of the concentration z. The activity of the solvent according [1] can be determined using Eq. (10) as
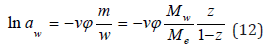
where φ is the osmotic coefficient of the solution. Using Eq. (4), the value of hi can be expanded in a Taylor series and limited to a linear term to represent it in the form
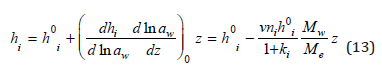
Substituting Eq. (13) into Eq. (11) we finally have
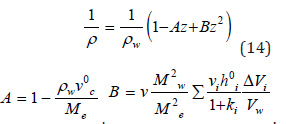
where
Next, we use the relationship of dimensionless concentration z with molality c. Combining equality c=m/V and Eq. (8), (9) we have
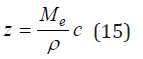
Substituting Eq. (15) into Eq. (14) and limiting to the quadratic term, we can determine the density of solution in the form
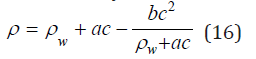
where a=Me A, b=Me2B.
Eq. (14) can be extended to mixed electrolyte solutions. If we neglect the influence of the last term Eq. (14), the density of the mixed solution can be calculated by the principle of additivity and is presented in the form
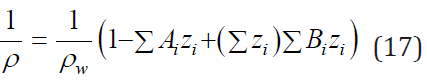
Further, using Eq. (15), (16), the density of the mixed solution can be expressed by molality
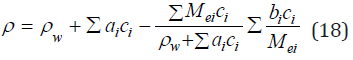
Discussion
Table 1 shows the applicability of the model used for electrolytes of various types. And in all cases, the main contribution of the linear term of Eq. (17) from which it is possible to calculate the partial molar volume of the electrolyte. To estimate this value, we present the volume of the hydrated complex as the sum of the volumes of the central ion and the surrounding water molecules where per one molecule of water accounts for a significantly smaller volume Vw*, then in structure of pure water Vw. Then Vhi = Vi + hiVw and the volume of solution can be represented as
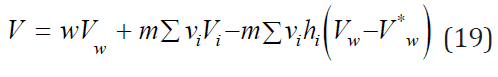
and further partial molar volume as
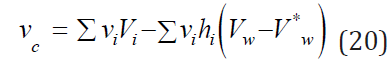
Table 1:The parameters of equation of aqueous solution (16) at 298K. *) at 298К; Δ is interval of concentration; δ is average approximation error; calculation according experimental data Ref. [3, 4].
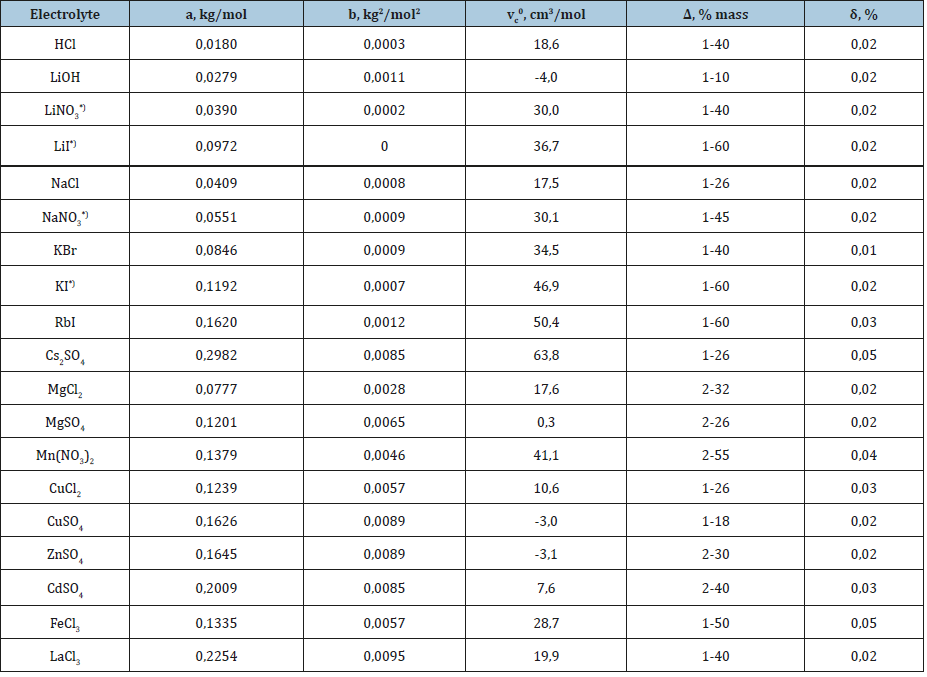
It is obvious that at high values of the difference ( Vw−Vw* ) the partial molar volume can even have negative values. Thus, this volume reflects structural change in the solution. Eq. (16) can be compared with the widely used Root equation [2].
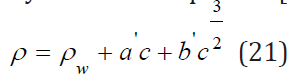
where the parameter a’ completely corresponds to the parameter a: ' 0 e w c a = M − ρ v . Hence, we can for each equation determined partial molar volume and compared these values with the experimental data (Table 2). For this purpose, we use Eq.(8) from where follows
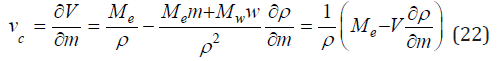
Further, determining the derived function
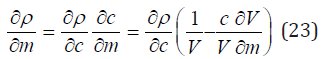
and substituting it into Eq.(22), we find
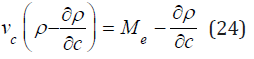
Using Eq. (24), we can determine the value of vc0 by extrapolation data ∂ρ/∂c to the field of an infinitely diluted solution at c ⤑ 0
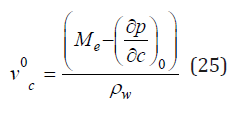
Table 2:The partial molar volume (cm3/mol) in aqueous infinite diluted solutions at 293K. The extrapolation error of experimental data [3,4] to the field of infinitely diluted solution is ±1cm3/mol.
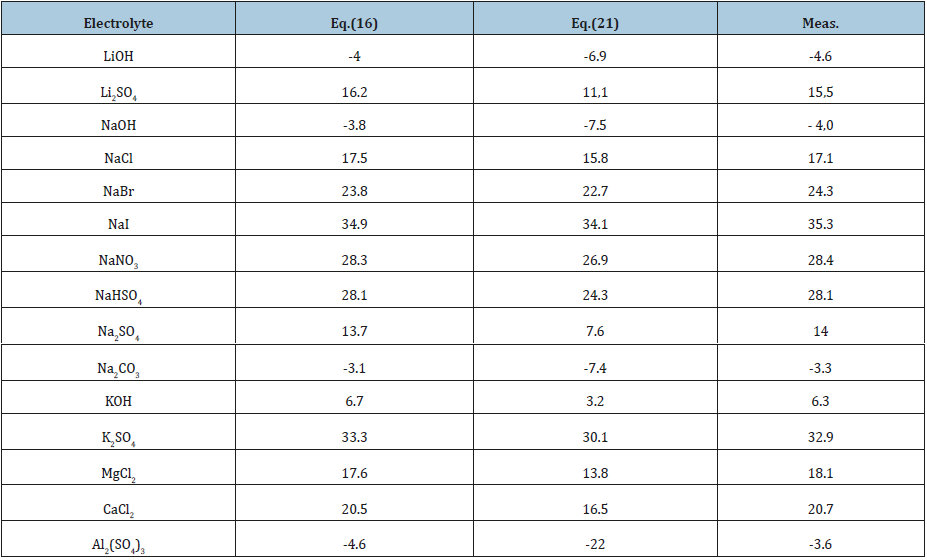
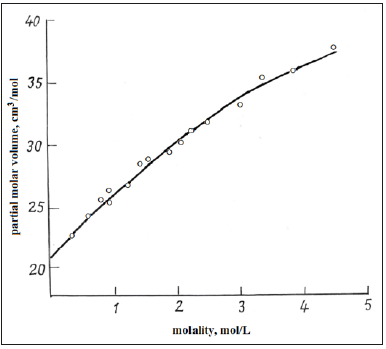
Figure 1 also shows the correspondence of the calculated values according to equations (16) and (24) and experimental data of partial molar volumes. Turning to the calculation of the density on mixed solutions should be noted that the Eq. (17), (18) are approximate because the initial Eq. (14), (16) are not linear. A strict solution can be obtained using as a starting Eq. (11) which turns into a linear one under the condition aw=const, since the value of hi according Eq. (4) depends only on the activity of the solvent. Then using the notation ρi*, zi* for binary isopiestic solutions, the inverse density of the mixed solution can be represented as a linear combination and expressed taking into account the boundary conditions as
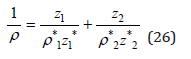
Figure 1:Partial molar volume of calcium chloride in aqueous solution at 298K. Experimental data and calculated curve.
where z1 and z2 are the concentration of components in mixed solution. However, the data in Table 3 show that the use of Eq. (17), (18) is a good approximation for calculating the density of mixed solutions and have significant advantage over Eq. (26), which requires a set of experimental data that is not always available.
Table 3:The density of mixed aqueous solutions LiNO3+NaNO3 and LI+KI at 298К.

Conclusion
Solvate model of solution leads to equations allowing to describe the density of electrolyte solutions with an accuracy acceptable for solving not only technological but also science problems [3-5]. The resulting equations using different concentration are convenient for the reverse calculation of the concentration reagents in the solution according to density data, which is of interest in the control of technological processes.
References
- Allakhverdov GR (2008) Thermodynamics of electrolyte solutions. Doklady Physica 53(8): 420-424.
- Root W (1933) The equation of density of the solutions. J Amer Chem Soc 50: 850-852.
- Sohnel O, Novotny P (1985) Densities of aqueous solution of inorganic substances. Phys Science Data 22, Amsterdam Elsevier New York, USA.
- Novotny P, Sohnel O (1988) Densities of binary aqueous solutions of 306 inorganic substances. J Chem Eng Data 33(1): 49-55.
- Mikulin GI (1968) Current issues in the physical chemistry of electrolyte solutions. In: Mikulin GI (Ed.), Leningrad, Khimiya Russia.
© 2019 GR Allakhverdov. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






