- Submissions

Full Text
Aspects in Mining & Mineral Science
Porosity, Specific Surface and Permeability in Micro-Inhomogeneous Media
Boris Sibiryakov*
Novosibirsk State University, Russia
*Corresponding author: Boris Sibiryakov, Trofimuk Institute of Oil-Gas Petroleum and Geophysics SBRAS, Novosibirsk State University, Novosibirsk, 630090, Russia
Submission: August 23, 2018;Published: September 05, 2018

ISSN 2578-0255Volume2 Issue2
Abstract
In the paper established clear formulas, which relate permeability with porosity and specific surface of pore and cracks. Shown that Darcy Law is not mandatory condition for calculation of fluid flow velocity. This Law may be able for one porous subject geometry and not be able for another one. The role of permeability plays a ratio between of a cube of porosity and quadrat of pores and cracks specific surface.
Keywords: The integral geometry; Porosity; Specific surface; Fluid flow velocity; Connectivity of cracks
Introduction
The prediction of stress-strain state in porous elastic body gives us the common state of medium only. For solving a problem about fluid flow and prediction of well production, it is necessary to calculate both stress-strain state in the skeleton and the pressure in the liquid. In this case, the gradient of pressure between formation fluids far from well and a pressure in the mud of well is a volume force, which tends fluid from productive layer into well, or, may be, in the opposite direction. Confronts of it the force of the viscous friction, which is proportional to specific surface and it concentrates into surface, which bounds skeleton and fluid. The equality of these forces provides a constant fluid flow velocity. To predict fluid flow velocity, it is necessary to have some data about structure of pore space, mainly specific surface and porosity. The structure of pore space describes by integral geometry characteristics. This discipline handles with collective characteristics (not individual ones) of complicate media. For isotropic bodies such parameters are four, not porosity only. There is a relation between specific surface of pores or cracks and the average size of microstructure , namely [1].

where f- is a porosity. A specific surface causes automatically the average size between one pore (crack) to another one, namely . In the fluid, there is analogous size I f . In papers [2,3] there is specific surface too. However, authors supposed that pore space represents as a set of elementary tubes, and this case is very special one. The thin tubes have great difference between Gaussian and average curvatures. The grain collectors have mentioned curvatures the same. The formulas in papers [2,3] authors contain empirical parameters with not clear physical and geometrical sense. Bio theory ignores structure of pore space (except porosity itself). He put into operation the permeability, which not related with pore space characteristics. It seems, the permeability should connect with porosity and specific surface. Last time created the computer technologies for calculation all four integral-geometric parameters, using Rontgen pictures all plane sections of samples [4-6]. These technologies give us the information about minimal sizes of samples, which are representative for heterogeneous media.
The target of a paper is to add Stokes equations to volume forces, due to viscous friction, and to get some elementary solutions of these new equations. The friction forces is surface ones. However, Stokes equations contain the volume forces. The main author assumption is that the volume forces are product of surface forces (frictions) into specific surface of sample. It gives the true dimension of volume forces and may be reasonable. For example, clays have a large porosity (up to 0.8), however the very large specific surface (five orders more than in sands) blocks any filtration processes.
The estimation of dissipative forces for grain skeletssssons
The surface force of viscous resistance 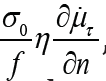 where is a tangent component of fluid velocity, and is a normal to the boundary
skeleton-fluid. The volume force of viscous resistance is
where is a tangent component of fluid velocity, and is a normal to the boundary
skeleton-fluid. The volume force of viscous resistance is
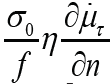 Try
to estimate the value of the normal derivative (s) 0 τ μ = . Expanding in
the Taylor series the fluid velocity, we can write
Try
to estimate the value of the normal derivative (s) 0 τ μ = . Expanding in
the Taylor series the fluid velocity, we can write 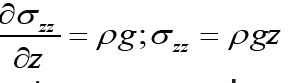 here a point means the center of gravity of elementary pore size.
Taking into account that (s) 0 τ μ = (due to viscous adherence), it is
evident that because the plane Laplace operator equal to
zero with the same reason. On the other hand, the Laplace operator
is proportional to the pressure gradient i.e
here a point means the center of gravity of elementary pore size.
Taking into account that (s) 0 τ μ = (due to viscous adherence), it is
evident that because the plane Laplace operator equal to
zero with the same reason. On the other hand, the Laplace operator
is proportional to the pressure gradient i.e
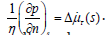 For
plane of the infinite sizes (practically for very small crack opening
compare to average length of a crack), a pressure with constant
gradient has not a vertical gradient
For
plane of the infinite sizes (practically for very small crack opening
compare to average length of a crack), a pressure with constant
gradient has not a vertical gradient
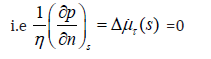
The same estimation there is on the more complicate surface,
if the radius of curvature of it much more, than thickness of film of
fluid, which provides a friction. Neglecting a small value of the third
order, we can write 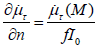 and the volume friction force takes
a form
and the volume friction force takes
a form 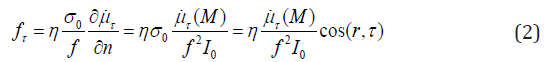
The friction force blocks of fluid flow for any sign of a cosine between the normal and the direction of fluid velocity. The average volume of friction dissipative force is
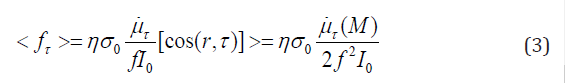
because the average number of the absolute value of cosine is a half. The equation of motion for cylindrical symmetry with a radial fluid flow takes a form
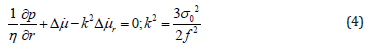
The estimation of dissipative forces in cracked media
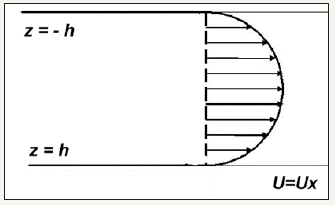
As the test problem for determine of dissipative forces on the crack levels we can use the well-known solution of a problem about percolation of fluid due to constant pressure gradient between two parallel planes with infinite sizes [7]. This situation is modelling the real percolation in the case, when a crack opening is very small compare to average length of crack. The flow velocity, which is equal to zero into boundaries, z=0; z=h is (Figure 1)
figure 1:The scheme of one-dimension fluid flow with constant velocity between two planes. On the boundaries z=+h the velocity is equal to zero, due to viscous adherence.

The average value of the flow velocity is equal to

The surface friction is
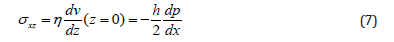
The volume friction force (for unit volume of fluid) is
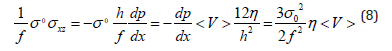
In [8] used the relation between a specific surface and a crack
opening in the form 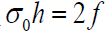 where is the porosity of cracked
medium. We need to average it with respect to any positions of
planes. Let do it. The average value of the local velocity < v> is the
product of macro velocity on the average cosine of a normal into
crack with cylindrical axe r namely
where is the porosity of cracked
medium. We need to average it with respect to any positions of
planes. Let do it. The average value of the local velocity < v> is the
product of macro velocity on the average cosine of a normal into
crack with cylindrical axe r namely

As to a volume dissipative force there is an expression
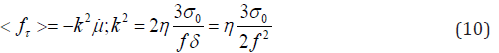
Thus, we have the same expressions for dissipative forces in porous and cracked media.
The infinite well in the half space. The equation of equilibrium for solid


For well of the infinite depth there is well-known solution of Lechnitzky [8]. He created that the tangent stress 0 rz σ ≡ not on the well surface only, but in the all space. The equations (11-12) are simplify as

The equation (13) can rewriting in the form
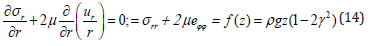
Where f (z) is the arbitrary function of the depth, and 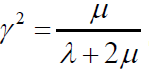 For large distances from the well an expression (14) must coincides
with horizontal stress in the infinite space without of well. It means
that in vicinity of the well there is plane incompressibility, namely
For large distances from the well an expression (14) must coincides
with horizontal stress in the infinite space without of well. It means
that in vicinity of the well there is plane incompressibility, namely
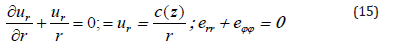
Strains on the well surface have a linear relation with respect to the vertical coordinate.

The equation of motion for the liquid
Using formula (10), we have a volume viscous friction force in the form

and the equation of fluid motion in the pore space, where the role of pore space plays the volume friction force is

One solution of the equation of motion
The plane incompressibility arrives with the same boundary
conditions in the all solid space i.е.
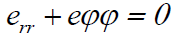 Neglecting the
vertical strain of productive layer, we can declare that there is plane
incompressibility in the liquid too
Neglecting the
vertical strain of productive layer, we can declare that there is plane
incompressibility in the liquid too 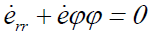 More accurate, we have an equality
More accurate, we have an equality 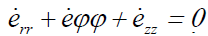 and the analogous formula for vertical strain is
and the analogous formula for vertical strain is 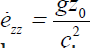 The ratio
The ratio 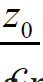 ,i.е. ratio of a velocity of
boundary moving into seismic velocity is negligible small. It means
that there is expressions
,i.е. ratio of a velocity of
boundary moving into seismic velocity is negligible small. It means
that there is expressions 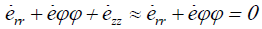 Thus, the
plane incompressibility there is both in solid and in liquid. Pay your
attention, that the Laplace operator in the equation (18) looks very
simple (due to common and plane incompressibility’s). Really
Thus, the
plane incompressibility there is both in solid and in liquid. Pay your
attention, that the Laplace operator in the equation (18) looks very
simple (due to common and plane incompressibility’s). Really
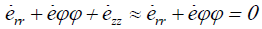
In equilibrium in half space with well there is a linear relation of displacement field ur
from the depth z, namely
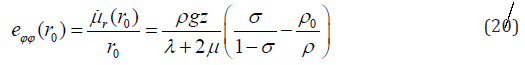
In (20) ρ is the rock density, r0 -the radius of a well,σ is
a Poisson ratio, and ρ0 is the mud density in the well. If the growing of pressure in fluid is the liner function too, the second derivative on the Laplace operator is zero. In another hand, (19) the plane part of mentioned operator may rewrite in more simple kind. Taking into account that
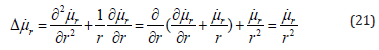
we can write, using a plane incompressibility, i.е.

The equations of motion (18) rewrites in the form

where C(z) is the arbitrary function. The integration with respect to r, gives
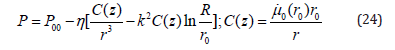
In (24) P00- is a pressure in fluid far from well, P0(z) is a pressure
of a mud in the well. Taking into account, that at r→r0 P→P0and
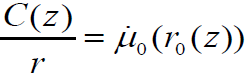 we get a relation between a pressure in the well mud
P0(z), a pressure in fluid far from well
P00 and the fluid flow velocity
0μ (z) in the form
we get a relation between a pressure in the well mud
P0(z), a pressure in fluid far from well
P00 and the fluid flow velocity
0μ (z) in the form

In formulas (24) and (25) the value R many times more, then diameter of a well, it is average horizontal size of the productive layer. In (25) a value 0μ (z) is required flow fluid velocity in the well
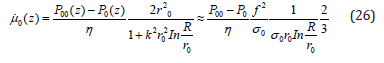
In denominator of (26) the value k2 is, as a rule, very large, compare to unit. Really,
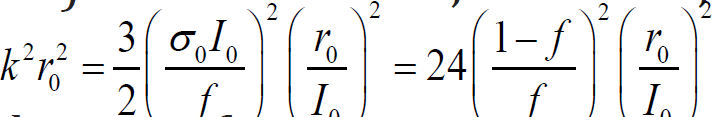
The formula (26) is true for infinite clusters only, i.е. for situations, when the elementary act of percolation (formula 5) there is in any point of medium. However, in the real sample there are some one-side open pores. In this pores a flow velocity is zero. The scheme, in according [5] is not possible. The infinite cluster is the pore system, without of one-side open pores. In finite clusters, the elementary scheme of percolation should be with some probability, which can relate with porosity
Existence or no existence of Darcy Law
For instances , which are small, compare to a well radius r0we can get analogous formula for plane flow (very large radius of a well), assuming R = r0 + x R. In this case

A formula (27) is the analog of Darcy law, where the role of permeability plays an expression
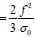
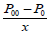
If the value x, is not very small compare to radius of the well, the relation (25) looks absolutely unlike of Darcy law. It means that Darcy law depends on fluid flow geometry. It may to be or may not to be. Another word, the Darcy law is a result of solved problem, but not a necessary part for the formulation of percolation problems.
The standard and percolation permeability. The elementary impermeable volume
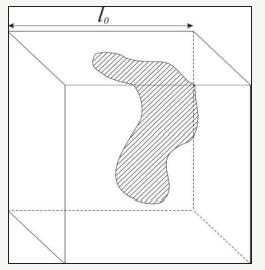
There is elementary impermeable volume, because there is an average distance between crack and it nearest neighbor I0. The model of percolation consists from cubes with cube edge I0 (Figure 2). Each of them is impermeable; however, a percolation there is on surfaces of mentioned cubes. If this this process is doing with unit probability, we have the infinite cluster and formulas (26-27) are true. However, this situation is rarely fact. The reason of it is, that the specific surface may be not small, in spite of very small porosity. It is evident that a small porosity means a small crack opening, and a percolation is impossible. There are closed channels on the some edges of the elementary cube.
figure 2:The percolation scheme of fluid flow with adjacent edges of the elementary cube. Inside of cube percolation is impossible
The relation between a specific surface and the average distance from crack to it nearest neighbor is giving by formula (1) of the integral geometry, and the product of a specific surface into crack opening δ is a double porosity, i.е.
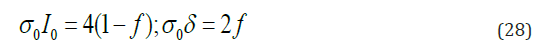
A part of pores corresponds to infinitely small crack opening,
though their specific surface not very small and good measuring
thing. In this case (at infinite small crack opening), the percolation
is impossible, and a formula (28) takes a form σ I * = 4 .It means
that all processes of percolation up to absence of them correspond
to diapason of structure linear size from
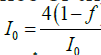 up to
up to 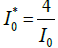 It may to relate the ratio of mentioned sizes
It may to relate the ratio of mentioned sizes
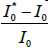 with probability
of percolation q, (size of structure I0=I0*means no percolation)
and it probability is
with probability
of percolation q, (size of structure I0=I0*means no percolation)
and it probability is 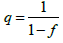 Evidently, it is true for sufficiently small
porosity. On the other hand, a porosity more than 0.5 really means
the change a space of skeleton and space of liquid. It corresponds to
absolute percolation. Thus the situation of elementary percolation,
which given by formula (5) is doing with some probability, and this
probability contains the porosity (from zero to 0,5) and a coherence
of elementary cubes.
Evidently, it is true for sufficiently small
porosity. On the other hand, a porosity more than 0.5 really means
the change a space of skeleton and space of liquid. It corresponds to
absolute percolation. Thus the situation of elementary percolation,
which given by formula (5) is doing with some probability, and this
probability contains the porosity (from zero to 0,5) and a coherence
of elementary cubes.
The coherence of elementary volumes
If the average distance between one crack and another one is
I0 the elementary impermeable volume is I0
3 and a percolation is
the runaround of elementary cube into his edges. It may arrive the
possibilities of flow from one edge to another one (favorable to
percolation) and flows of closed contours on one of edge of cube
(unfavorable for percolation). The probability to have a flow from
one edge to another one related with probability of crossing of
plane section perimeter of body (projection of the crack perimeter
to the plane) with an edge of the elementary cube. Examine a
mentioned cube with an edge I0. The specific surface of cube is
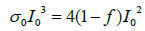 The fluid volume in an elementary cube is f03
.The average thickness of fluid gives by a formula
The fluid volume in an elementary cube is f03
.The average thickness of fluid gives by a formula
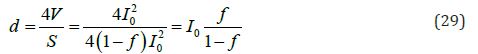
There is in the integral geometry a relation between specific
surface of three-dimensional body and perimeter of it twodimensional
plane section. One of these sections may be as an edge
of an elementary cube. The average perimeter of two dimensional
curve (it may be not closed) on the plane, (which is equal to
I02 according to the formula
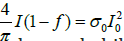 is equal to 0 I =π I . The
coherence or not it gives by probabilities of crossing of plane
perimeter 0 I =π I with the cube edges I0 (Figure 3).
is equal to 0 I =π I . The
coherence or not it gives by probabilities of crossing of plane
perimeter 0 I =π I with the cube edges I0 (Figure 3).
figure 3:The relation between of the number of intersections of adjacent edges of elementary cube with the perimeter of a plane crack projection. On the figure presented the evolvent of adjacent edges of an elementary cube, which provides a percolation. The average number of crossing of edges, (in this case 4) relate with the length of plane projection of crack l, and it may be determine from specific surface.

The another formula of the integral geometry relates the
average number of crossing points of perimeter of a plane crack
projection, with edge of a cube is a little bit more, than four., namely
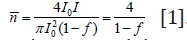 The percolation provides at two crossing
points as a minimum, because is arriving one channel (two levels)
either sender or sink
The percolation provides at two crossing
points as a minimum, because is arriving one channel (two levels)
either sender or sink
(Figure 4) (One crossing point is not create a channel). In
average, on the one of edge of a cube is arrive one sender and one
sink. In the uniform distribution of probabilities of crossing the
function of distribution is linear one, his average value is
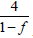 and a probability to have two and more channels is
and a probability to have two and more channels is
 If we exclude
probabilities of sender and sink coincides (Figure 4) this probability
decreases in two times. On the Fig.4 points correspond to channel,
crossing an edge of cube, and bars correspond to returned
situations, i.e. coinciding of sender and sink. The probability of
passing of the elementary cube is p=gp i. e. the probability , which
product into probability of coherency
If we exclude
probabilities of sender and sink coincides (Figure 4) this probability
decreases in two times. On the Fig.4 points correspond to channel,
crossing an edge of cube, and bars correspond to returned
situations, i.e. coinciding of sender and sink. The probability of
passing of the elementary cube is p=gp i. e. the probability , which
product into probability of coherency  In this case the role of permeability plays not expression
In this case the role of permeability plays not expression (as for infinite cluster), but the more less value, taking into account one-side pores (Figure
5).
(as for infinite cluster), but the more less value, taking into account one-side pores (Figure
5).

figure 4:Probabilistic trajectories of returned fluid flow (bars) and trajectories into another elementary cube, i.е. probabilistic вероятная percolation trajectory (points). The first of them (probability of returned flow) at small porosity a little bit less, than 0.5, and second of them a little bit more, than 0.5.
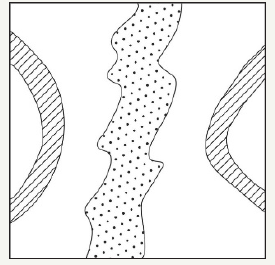
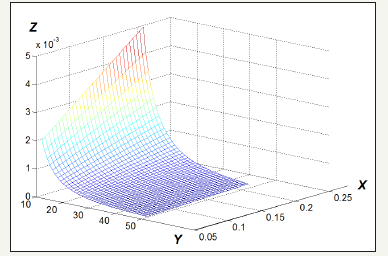
figure 5:The relation between probability versus porosity and specific surface of cracks. On the axe x is the porosity, on the axe y is the specific surface (inverse centimeters) on the axe z is the permeability (quadrat of centimeters). The role of permeability plays the multiple which is proportional to the cube of porosity and inverse proportional to quadrat of specific surface of sample.
Formula (30) closed to empirical relation, made experimentally
Fallini [9], namely, 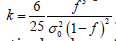 The empirical of Fallini constant
The empirical of Fallini constant 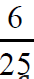 closed to theoretical value of this paper
closed to theoretical value of this paper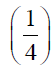 and the structures of expressions for permeability are the same. Quadrat of specific
surface in denominator gives the true dimension of permeability.
The great specific surface may be eliminate any filtration, even by
high porosity.
and the structures of expressions for permeability are the same. Quadrat of specific
surface in denominator gives the true dimension of permeability.
The great specific surface may be eliminate any filtration, even by
high porosity.
Conclusion
1. The model of structured continuum gives us a possibility to relate the viscous friction forces with specific surface of pores and cracks, not using Darcy law. This law can create from usual conditions of elastic equilibrium for skeleton and uncompressible viscose fluid. The Darcy law may to be, or not to be, depends on geometry of flowing.
2. The flow velocity depends on rupture of skeleton and fluid pressures, mainly by stresses in skeleton. This rupture is special problem.
The role of permeability plays the ratio of cube of porosity to quadrat of specific surface of pores and cracks.
References
- Mecke J (1983) Santalo L integral geometry and geometric probability (Encyclopedia of mathematics and its application). 59(6): 286-286.
- Carman PC (1956) Flow of gases through porous media. Butterworths, London, UK.
- Robert PC, Michel A (2003) Predicting the coefficient of permeability of soils using the kozeny carman equation.
- Arns CH, Knackstedt MA, Mecke KR (2004) Characterization of irregular spatial structures by parallel sets and integral geometric measures.Colloids and Surfaces A: Physicochemical and Engineering Aspects 241(1-3): 351-372.
- Bazaikin Y, Gurevich B, Iglauer S, Khachkova T, Kolyukhin D, et al. (2017) Effect of CT image size and resolution on the accuracy of rock property estimates. Journal of Geophysical Research: Solid Earth 122(5): 3635- 3647.
- Zhang D, Zhang R, Chen S, Soll WE (2000) Pore scale study of flow in porous media: scale dependency, rev, and statistical REV. Geophys Res Lett 27(8): 1195-1198.
- Landau LD, Lifschitz EM (1986) Hydrodynamics. Moscow, Russia, p. 736.
- Lechnitzky SG (1938) Plane problem of elastic theory for bodies with cylindrical anisotropy. Annals of Saratov university N I (XIV): 2.
- Pierpaolo F (2004) Elettrosmosi nel_CANTIERE edile. Chimica Industrial, p. 35.
© 2018 Boris Sibiryakov. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






