- Submissions

Full Text
Annals of Chemical Science Research
Physicochemical Mechanics and Colloid Science
Kocherginsky NM*
Next-ChemX, University of Illinois at Urbana-Champaign, USA
*Corresponding author:Kocherginsky NM, Next-ChemX, University of Illinois at Urbana-Champaign, USA
Submission: April 17, 2023;Published: June 07, 2023

Volume4 Issue2June , 2023
Abstract
Suggested by us physicochemical mechanics is based on mechanical ideas simple and intuitive unifying approach to describe all major laws of equilibrium and nonequilibrium thermodynamics including kinetics of elementary chemical reactions far from equilibrium. In this paper we suggest a new equation for chemical transport that generalizes the equilibrium Gibbs-Duhem equation. Using physicochemical mechanics we further demonstrate how it is possible to derive many classical equations of colloid science, including the Gibbs adsorption isotherm, the relationship between surface energy and curvature, the Young-Laplace equation, Kelvin’s equation for partial vapor pressure above a curved surface, the Ostwald equation describing the solubility of solid particles in liquid, the Gibbs-Thomson equation describing the increase of boiling temperature as a function of curvature, the Clausius-Clapeyron equation for vaporization, sublimation and fusion, Rehbinder’s effect for materials mechanics, the relation of the applied electric potential with the surface tension and the Lippmann and Frumkin electrocapillary equations. In all cases, we use the same mobility suggested by Einstein to describe Brownian motion. Now, based on mobility or the rate of any one transport process, using known molecular constants we can calculate the rates of all other transport processes and their equilibrium without additional experiments and computer simulations.
Keywords:Physicochemical mechanics; Equilibrium and nonequilibrium thermodynamics; Colloid phenomena fundamentals; Mobility
Introduction to Physicochemical Mechanics
As is clear from its name, Gibbs equilibrium thermodynamics deals with equilibrium states, initial and final, therefore it does not tell how fast equilibrium is reached. Time is not present as a variable in equilibrium thermodynamics [1]. Linear nonequilibrium thermodynamics is based on the rate of entropy production, and its main postulate tells that not far from equilibrium the flux is a linear function of so-called “thermodynamic forces” [2]. These “forces” have different units, not Newtons and cannot be added. As a result, it is not a trivial task to derive classical equilibrium relations. The major achievement of nonequilibrium thermodynamics is the statement known as the Onsager reciprocity relation. According to it, if there are several fluxes i driven by the same set of thermodynamic forces j, in the matrix of equations describing all fluxes mutually symmetric phenomenological coefficients in front of the forces are equal, i.e., Lij = Lij. [3,4]. When i ≠ j , nonsymmetrical coefficients Lii and even their signs are often not known.
Previously we suggested another approach, which we call physicochemical mechanics. This approach is based on well-known mechanical principles and suggested by Einstein mobility. It allows for a simple derivation of all major classical physicochemical equations, both for the rates of transport processes, and their equilibrium [5]. It easily leads to the Onsager reciprocal relations, and it also gives the relation of all phenomenological transport coefficients [6]. Moreover, far from equilibrium it leads to equations similar to the theory of the activated complex for elementary chemical reactions [7]. Chemical transport is often driven by one driving factor such as concentration, pressure, voltage, etc. Specifics of colloid processes are that they may be driven by three additional driving factors, such as gradients of surface tension, specific molar surface and even curvature. In this paper we briefly remind the reader of the major ideas of physicochemical mechanics and then we demonstrate how to use it in the derivation of major equations of colloid science, which has not been done before.
According to the Newton’s second law, acceleration of a moving body of i-th type driven by j forces is described by miai =ΣjFij . Dealing with molecules, it is convenient to use molar concentration ci (mol/L), so that each of the terms Fij is a molar force with the same units of Newton/mol. In a condensed system there is also a friction force. It has the direction opposite to the sum of the other forces, and usually it is proportional to velocity, which is known as Stokes’ law, Ffriction = −ki vi .Transport very quickly reaches the steady state where the friction force balances the total of the other forces, and thus ai=0, and vi=1/kiΣjFij.ki is proportional to viscosity and depends on body’s size and shape. The flux of many particles of the same type with the units of mol/area × time is
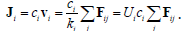
All j terms in the total force are multiplied the same mobility coefficient Ui , suggested by Einstein to describe Brownian motion. It is inversely proportional to viscosity and may be interpreted as the velocity per unit of molar force. Taking each of these j terms separately leads to related transport equations. For example, the flux (mol/cm2sec) in the x-direction of an ion with the molar charge qi , driven by a gradient of an electric field dψ / dx , is
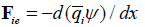
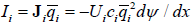
Classical thermodynamics gives the relation of changes of chemical potential and molar entropy. At constant temperature it is
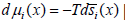
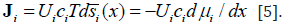
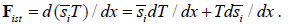
For one component in non-isolated system instead of traditional chemical potential we may introduce more general physicochemical potential μgi such as:
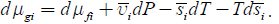
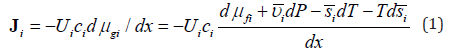
It includes entropy-related and fields-related terms. Thus, we see that suggested previously and based on physicochemical potential approach [5] is closely related to molar entropy-based description. Each term in the nominator of equation 1 has units of molar energy and its negative derivative over coordinate has the units of force. In most common cases the energy components may be presented as a product of an intensive molar property by an extensive variable, such as constant molar charge by electric potential or constant molar volume by pressure. The situation is more complicated for a product molar entropy by temperature. In the presence of temperature gradient molar entropy also is a function of coordinate and the two last terms describe thermal and entropic forces.
Now consider transport driven by two driving factors simultaneously, for example, by a concentration gradient and the gradient of electric field. Without equilibrium, the molar transport driven by the gradients of chemical and electric potentials may be presented as
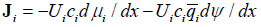
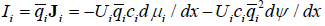
In simple equilibrium, the two fluxes due to two driving factors should balance one another. For concentration and potential gradients this means

Transport and inversed Gibbs-Duhem equation
The variables held constant in a process are termed the natural variables. With adequately chosen natural variables related thermodynamic functions decrease in a spontaneous process. For example, Gibbs free energy G has natural variables T and P. It is easy to control temperature and pressure, which makes G an especially valuable function, which decreases in isobaric-isothermal processes in an isolated system. In the presence of electric and other fields, including pressure and temperature gradients, for multicomponent system we may introduce a new general function, Gg , such as
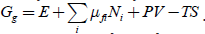
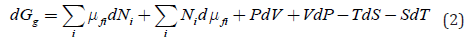
In transport the role of intensive natural variables and their conjugated molar properties changes to the opposite in comparison to chemical processes. It is possible to apply a pressure gradient, temperature gradient, or electric field to a solid membrane and observe chemical transport, though extensive system volume or charge of transported ions do not change. To describe transport in space, we need only a part of equation 1 with differentials of intensive variables, i.e.,

In addition, transport leads to changes of local concentrations, and it means local entropy. Thus, the correct equation should have an additional term -TdS :
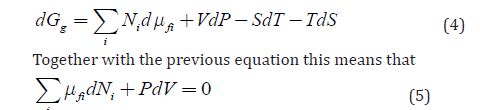
After comparison with the complete differential (equation 1), this equation simply tells that the changes of composition due to i dN lead to changes of volume and vice versa. There is no contradiction between this and the well-known for chemical thermodynamics Gibbs-Duhem equation ΣiNidμi −VdP + SdT =0 because the first is the result of a g G -related vectorial transport process and the second describes equilibrium of internal scalar chemical processes.
Derivation of basic equations of colloid chemistry
The possibility of using conventional non-equilibrium thermodynamics for interfaces is not obvious, which was recognized by Prigogine [9] and later in [10]. We suggest adding an additional term to physicochemical potential, which is the product of effective local surface tension σ by molar surface area a . The specifics of interface processes are that both the gradients of surface tension and curvature may be driving factors. In addition, in some processes a also may change. All thse factors may be easily included in physicochemical mechanics-based description. For simplicity we neglect possible hydrodynamic effects, and assume that heat transport does not change the temperature distribution, though both these effects may be important for colloid systems [11- 13]. If all other driving factors are also constant, the rate of lateral transfer of an adsorbed component due to the gradient of surface tension should be
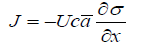
Here c is local concentration near the surface. It is easy to describe the equilibrium of processes driven by surface tension and any other driving factor, such as concentration, pressure, electric field and temperature. In the first case, balance with the described by Fick’s law flux if curvature and molar surface area a is constant gives
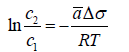
This equation can be rewritten in a differential form, known as Gibbs adsorption isotherm:
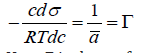
Here Γ is the surface concentration. For a pair pressure and surface tension as driving factors at equilibrium
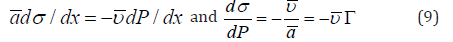
After integration for a spherical droplet with radius r this gives an analog of Young-Laplace equation [12]:

For a droplet of arbitrary shape, one has to use a tensor-based description with three coordinates [13]. In this case one could introduce invariants of a tensor, i.e., scalar functions of the tensor components which remain constant under a basis change. This invariant has the same value when computed in two arbitrary bases, a Cartesian and some other basis. A symmetric second order tensor always has three independent invariants, but they do not help analysis of transport in condensed systems where pressure and external forces depend on coordinate.
Adsorption of a surface-active substance and its subsequent penetration decreases σ on the surfaces of solid granules and in preexisting minor cracks inside the solid. This leads to smaller inter-particle interactions, disjoining pressure and finally, reduces the material’s mechanical strength. It is even possible to break a wedding gold ring simply by covering it with thin films of Hg. This mechanical phenomenon induced by physicochemical interactions is known as the Rehbinder’s effect, who also called it physicochemical mechanics [14]. Similar description is valid for a balance of surface tension and gravity. Onboard the International Space Station the weightless water can form big floating drops and even films/membranes, which are stable inside a wire ring for many hours.
Balance of surface tension and electric potential gives the Lippmann equation, usually used to analyze an electric double layer and electrocapillary maximums

In a solution we have qi = ciqi = ciziF . For electrocapillary phenomena i q is generated by one ion charge of unit surface and ψ - its electric potential. Changes in applied electric potential lead to the changes of surface tension, and the negative slope reaches its zero maximum when the surface charge is zero. This zero charge potential is an essential characteristic of electrode kinetics, especially for polarography with dropping mercury electrodes.
When a changes at constant σ , balance of surface curvature effects and electrical forces is described by
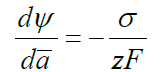
Further, we will consider major processes due to the surface curvature when the surface tension is constant. After integration for a sphere, we have

Changes in electric potential with size play a crucial role in colloid stability, nanoparticle electro-separation, electrocapillary effects and polarography with dropping mercury electrodes. In a multicomponent system where noncharged species j may be also adsorbed on the surface, we should talk about reversable work dA to increase surface area by one unit. In this case in equilibrium, we have a balance of three driving factors, and
Figure 1:A la Picasso portrait of A. N. Frumkin, made by his pupil O. Petrii and R. Marvet at Lomonosov Moscow State University, electrochemistry department. All major curves and a capillary with mercury drop are taken from Frumkin’s electrochemical papers.

Here we should mention that electrophoresis of colloid particles is described based on electrophoretic mobility Ue , which is the particle velocity for a field strength 1volt/cm. In this case an assumption that an electric force is balanced by viscous drug force described by Stokes equation leads to the Hückel equation
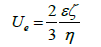
Note that when electrophoretic mobility is presented as a function of ζ -potential, it does not explicitly depend on the particle size, which is different to Einstein’s mobility. The coefficient is not necessary 2/3 and it is sensitive to particle shape and double layer thickness [12].
In general, it is the ratio 2σ / r , which plays the role of a driving factor for a sphere. In this case, small changes δ of this ratio are

The flux due to the changes of r should be proportional to −Ucv2σ/r2 . A species has higher energy on the surface with higher curvature and will move to the flat area. This effect is essential for transport along nonhomogeneous and bent bio-membranes. For a flat surface, the curvature 1/r is zero, and the flux disappears. In equilibrium, this flux must be counterbalanced by concentrationdriven flux. After substitution into two expressions for fluxes mobility cancels giving
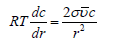
Integration from r to ∞ using partial pressure for vapor instead of concentration (at equilibrium they are proportional) gives Kelvin equation for partial vapor pressure above the curved surface:

A similar equation, known as the Ostwald equation, describes the solubility of solid particles in liquid. The plus sign refers to a convex surface, while a concave surface should have the minus sign. For a pair pressure and temperature as driving factors at equilibrium we have Clausius-Clapeyron equation
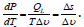
Balance surface structure gradients and surface effects is essential for evaporation or condensation through the drop surface. If molar entropy and temperature gradient does not change with time, the rate of mass transfer from the liquid phase to vapor is:
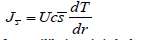
In equilibrium it is balanced by the surface tension-driven flux, which gives
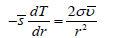
At constant surface tension and using the approximate relation s = ΔHvap /T , after integration from initial r to ∞ and from T to the boiling temperature Tb, we have an analog of the Gibbs-Thomson equation describing the increase of boiling temperature as a function of curvature:
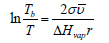
similar equation describes the melting point decrease for nanocrystals or crystals in pores. If the surface tension changes with r , which is also important for nanomaterials, we can use an approximate relation

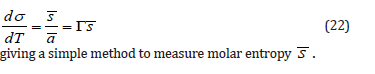
Conclusion
Albert Einstein in Herbert Spencer Lecture, “On the Method of Theoretical Physics”, given in Oxford, June 1933, wrote: “The supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible.” Later in 1936, the paper “Physics and Reality” he wrote: “The whole of science is nothing more than a refinement of everyday thinking” [16]. Here we demonstrated that a few simple ideas from physicochemical mechanics lead to many well-known classical laws of colloid chemistry and related transport processes. One does not have to memorize many different laws. It becomes possible not only to easily derive them but also see their interrelations. More specific examples of other applications in colloid chemistry, including kinetics of colloid coagulation and micelle extraction, phase rule in the presence of fields, kinetics of the first order phase transitions and formation of a new phase embryos and kinetics of the second order phase transitions and critical phenomena are described in our book [17].
Suggested by Einstein to explain Brownian motion mobility and forces-based physicochemical mechanics give well-known and experimentally proven equilibrium equations in colloid science. This shows that the same mobility applies to the volume near the surface and surface processes. If the proportionality coefficient were different in front of the gradients of different driving factors, we would not get the correct equations for equilibrium states. Based on the rate of just one transport process we can calculate mobility, and then, using molecular constants we can calculate the rates of other transport processes without experiments and computer simulations.
Declaration of Interest
The authors have no competing interests to declare. No financial support was provided for the research and preparation of the article.
References
- Kondepudi D, Prigogine I (1998) Modern thermodynamics, from heat engines to dissipative structures. J Wiley, Chichester, UK.
- Callen H (1985) Thermodynamics and an introduction to thermostatics. In: (2nd edn), John Wiley & Sons, New York, USA.
- Prigogine I (1961) Introduction to thermodynamics of irreversible processes. In: (2nd edn), John Wiley & Sons, New York, USA.
- Le Bellac M, Morteffagne F, Batrouni GG (2004) Equilibrium and non-equilibrium statistical thermodynamics. Cambridge University Press, Cambridge, UK.
- Kocherginsky NM, Gruebele M (2016) Mechanical approach to chemical transport. Proceedings of the National Academy of Sciences of the United States of America 113(40): 11116-11121.
- Kocherginsky NM, Gruebele M (2013) A thermodynamic derivation of the reciprocal relations. Journal of Chemical Physics 138(12): 124502.
- Kocherginsky NM (2010) Semi-phenomenological thermodynamic description of chemical kinetics and mass transport. Journal of Non-Equilibrium Thermodynamics 35(2): 97-124.
- Kocherginsky NM, Gruebele M (2021) Thermo-diffusion: The physicochemical mechanics view. Journal of Chemical Physics 154: 024112.
- Defay R, Prigogine I (1966) Surface tension and adsorption. J Wiley, New York, USA.
- Roldughin VI (2012) Nonequilibrium thermodynamics of colloidal systems. Russian Chemical Reviews 81(10): 875-917.
- Tovbin Yu K (2019) Small systems and fundamentals of thermodynamics. CRC Press, Boca Raton, Florida, USA.
- Hunter RJ (1995) Foundations of colloid science, v. 1,2. Oxford: Clarendon Press.
- Krotov VV, Rusanov AI (1999) Physicochemical hydrodynamics of capillary systems. Imperial College Press, London, UK.
- Rehbinder PA (1958) Physico-Chemical mechanics. Science. Moscow, Russia.
- Frumkin A (1923) On the theory of electrocapillarity. I. Capillary electric phenomena in non-aqueous solvents. Z Phys Chem 103U(1): 43-54.
- Einstein A (1936) Physics and reality. Journal of the Franklin Institute 221(3): 349-382.
- Kocherginsky NM (2023) Physicochemical mechanics with applications in physics, chemistry, membranology and biology. Cambridge University Press, Cambridge, UK.
© 2023 Kocherginsky NM. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






