- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Annals of Chemical Science Research
Density Functional Theory in Biology
Phelecia Scotland and Preet Sharma*
Non-Linear Science Research Group, Department of Chemistry & Physics, Midwestern State University, USA
*Corresponding author: Preet Sharma, Non-Linear Science Research Group, Department of Chemistry & Physics, Midwestern State University, USA
Submission: May 07, 2020Published: May 18, 2020
Volume2 Issue1May, 2020
Abstract
The density functional theory is a very strong tool in quantum mechanics which deals with many body problems and how to solve them. We give a mini review of the very basics of the theory behind this theory in this study.
Introduction
Density functional theory was created to calculate and analyze the electronic structure of quantum and solid-state structures that are of interest in solid state physics and chemistry [1]. It is a hybrid of quantum mechanics and molecular mechanics. It utilizes quantum mechanics to describe regions of high priorities in a system. This method is usually very accurate when the right parameters are used. Additionally, DFT uses molecular mechanics force fields to describe the remaining atoms in the system [2]. This method does not need to be as accurate since it is not used on the region of focus. The improvements made to DFT during the late twentieth century have expanded its application across the disciplines of chemistry and physics. Most recently, these calculations have been used to describe biological molecules. However, even the simplest biological molecules tend to be large compared to those studied in physical science. Therefore, the computational cost would be exuberant if other Ab inito methods were used. DFT can be applied to these large systems because it offers a good balance between accuracy and computational cost.
The foundation of DFT was established by Hohenberg [1] & Kohn [2]. Their theorem states that the ground state energy, which can be found using the Schrodinger’s equation, is a unique functional of the electron density. Additionally, the ground state energy of the system can be obtained by minimizing the energy of the system according to the electron density. This provides an appealing and more versatile alternative, as it provides a way to systematically map the many-body problem. DFT takes into consideration the various interactions in the system. The exchange energy and the correlation energy of the system tends to be difficult to calculate and interpret. Therefore, DFT a powerful analytical tool is able to create approximate predictions of these terms and contributes to a more accurate ground state energy term. The problems of DFT are continually studied. The use of more parametrized density functionals have also been used to solve existing problems.
Application of Density Functional Theory in Biology
Very recently, the density functional theory has been useful in applications to complex biological systems [3]. For example, before an enzyme binds to it substrate there is an energy associated with its natural state. There is also a different energy term that is associated when the enzyme binds to its substrate and one when it releases the substrate. By applying DFT to each state of the system, the different energy terms can be determined. Therefore, this is the first step in understanding the energetics of protein systems. If the high priority regions of a protein are selected and coupled with DFT application to various states, it is possible to determine the difference in energy of a functioning and misfolding protein. Subsequently, it may be possible to determine the site of protein misfolding which is useful for the study of tumor growth research. There are many situations in which the density functional theory can be applied. There are several reasons for introducing density functional theory to understand complex systems in biology. We need to understand how the interatomic interactions play a role and how we can model it more accurately rather than the force field scenario [3]. The main reason is that there are many interactions happening simultaneously in a biological system which have to be modelled together.
Fundamental Aspects of Density Functional Theory
The basics of density functional theory use the interactions between systems using applications of the following theory [4]:
Schrodinger Equation
For a many-electron system the many-body Schrodinger equation is given as,
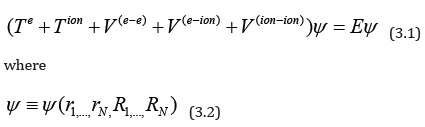
The kinetic energies are given by,
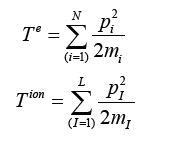
and the potential energies are given by,
\
Basics of Kohn-Sham theory
This theory says to replace the original many-body problem with an independent electron problem so that it can be solved. Only the ground state density and the ground state energy are required to be the same as in the original many-body problem.
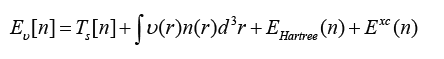
Conclusion
This methodology has been regularly applied in physics and chemistry. Since complex biological systems have many interactions happening simultaneously so the density functional theory is a very strong tool to explore.
Acknowledgment
One of the authors, Phelecia Scotland gratefully acknowledges the financial support of the Robert Welch Foundation (Grant #A0 - 0001).
References
- Hohenberg P, Kohn W (1964) Inhomogeneous electron gas. Phys Rev 136: B864.
- Kohn W, Sham LJ (1965) Self-consistent equations including exchange and correlation effects. Phys Rev 140: A1133.
- Andreoni W, Curioni A, Mordasini T (2001) Dft-based molecular dynamics as a new tool for computational biology: First applications and perspective. IBM Journal of Research and Development 45(3-4): 397-407.
- http://helper.ipam.ucla.edu/publications/maws3/maws3 5873.pdf
© 2020 Prasad DSN. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version