Long-term Data–the Key for Evaluating Runoff Peak Discharge Estimation Tools and Parameters for Watersheds on Forest Lands

Forests are recognized as an integral component of the landscape, and maintaining their functional integrity is fundamental for the sustainability of ecosystems and societies alike [1]. In the U.S., forests cover about one-third of its land [2,3], totaling about 300million ha [4]. In recent years, there has been considerable public attention toward understanding the hydrological and ecological functions of forested landscapes [5], particularly in response to land use change and climate change (CC). In many areas of the U.S., contemporary landscapes are a mosaic of agricultural, forest and urban lands. These lands are facing environmental issues including landslides, flooding, soil erosion, water quantity and quality degradation, and ecosystem service losses [6]. This may be happening potentially due to increasing frequency of extreme precipitation by warming climate predicted by most CC models [7] and supported by the record over the last 50years [8]. Reliable tools and techniques, analogous to those developed to improve agricultural production, design and manage road and water infrastructure and quantify their environmental impacts are needed also to ensure the sustainability of the forested landscapes and ecosystem services (soil, water, timber etc.) in the face of the climatic extremes. Much of the published research on forests including USDA Forest Service long-term experimental forests and ranges (EFRs) have focused on relationships among forests, water, hydrologic processes and watershed management, fire, productivity, and other ecosystem services [9-12], with only limited information on engineering hydrologic design aspects required on forested landscapes in the face of climate change [13].

A large number of hydrologic design and application tools exists in literature for the assessment of precipitation intensities and duration, storm runoff volumes, and peak discharge rates often used for design in culverts, bridges, and other road infrastructure including detention storage, and stormwater management practices [14]. The SCS-CN [15] method for assessing direct runoff (Q) and the Rational Method [16] for calculation of peak discharges (Qp) are excellent examples of such tools that have been widely used and modified for multiple applications in US and abroad for above purposes. Accordingly, a plethora of literature also exists about methods, validation, and limitations of both of these methods and their parameters mostly for the agricultural and urban landscapes. However, these methods previously derived for agricultural land s have been “imported” or applied directly to forested/woodland conditions with very limited validation, resulting in large uncertainties [17]. The same is true for the Rational Method originally developed for small urban areas. Such uncertainties may arise mostly from incorrect model parameterization related to forest catchment characteristics like microtopography, canopy, surface, and subsurface storage, heterogeneous under- and over-story surface vegetation, channels with complex morphology, higher slope in some cases etc. Most of these parameters affect processes like rainfall interception, infiltration, antecedent soil moisture, evapotranspiration, surface and subsurface flow, their pathways etc., ultimately influencing the Q and Qp. Thus, limited validation studies on forest catchments may be due to a lack of data and lower priority for such studies on forest lands until recent decades. In addition, designers/ planners in engineering hydrology field may have limited knowledge about the long-term hydro-climatic data available from the USDA EFRs and similar others across various ecoregions in the nation. Only a few recent studies [17-20] have tested those tools and parameters using limited data from some of the EFR watersheds (Figure 1).

Figure 1: Location of 10 USDA Forest service experimental forest watersheds [10].

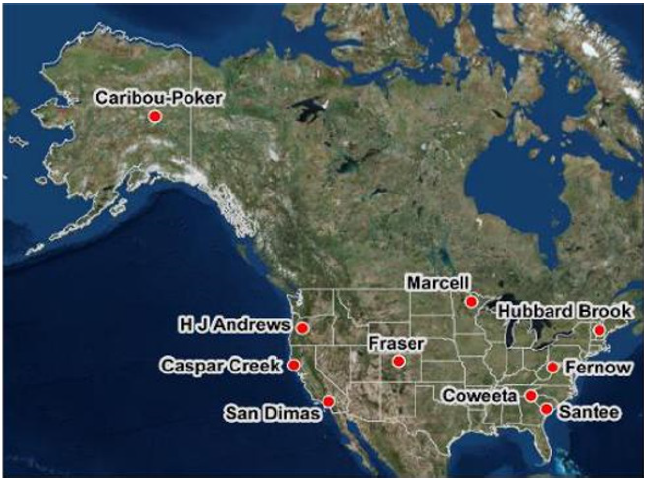
Through a series of examples and new analyses, the value of USDA long-term data on watersheds, forests, and ranges in understanding key ecohydrological issues, including (a) time lag between causes and effects, (b) critical thresholds and cyclic trends, (c) context of rare and extreme events, and (d) mechanistic feedbacks for simulation modeling has been demonstrated [18] . Correspondingly, recent studies using the SCS-CN models with limited 4-year (2011-2015) data from three EFRs in the Southeastern U.S. (Figure 1) have shown both over or underestimation of Q or Qp on forest watersheds. Those studies [21,22] also showed that modification of the existing SCS-CN method and their parameters can improve predictions if necessary rainfall-runoff data for a long time period are available.

In this opinion piece, we propose validation and possible improvements of the tools and methods described above or even a possibility for developing/testing novel approaches using the available long-term data from the EFR watersheds (Figure 1) and similar other sites (USGS, Universities, Weyerhaeuser etc.) for reliable assessment of Q and/or Qp in forest watersheds. These data combined with catchment and vegetation characteristics derived from ultra-high resolution LiDAR and satellite imagery data will also allow for evaluating and improving model parameters on various forest conditions, while adding new parameter information for enhancing predictions of Q and/or Qp for sustainable management road and water management infrastructure on the forest lands. For example, the USDA Forest Service itself manages 193 million acres of public lands [20] and a road system consisting of approximately 595,700km (370,000 miles) of roads and at least 40,000 stream crossings [23], that are susceptible to wide-ranging climate change impacts in every region of the country including on roads, bridges and other transportation infrastructure needed to access those forested lands. Descriptions of some of the EFR sites and available data can be found elsewhere [10-12,18,19,21,20]. Similarly, real-time climatic data for some of the EFRs are also available at https://smartforests.org/content/smart-forests-data. Related data packages are available from USDA Forest Service at htps:// www.fs.usda.gov/rds/archive/catalog/.

PIDF curves

We propose that the NOAA published Atlas-14 maps [24,25] for precipitation intensity duration frequency (PIDF) curves obtained by regional interpolation of several rain gauges in the network be reevaluated with EFR on-site local regional PIDF data when applying them in the Rational Method and others for design discharge estimates used in design of structures on the Forest Service EFR lands and roads. Most of the EFRs have their own long-term (>50yrs) precipitation data for multiple gauges exceeding 50years, which, in many cases, are not used in the NOAA gauge network analysis.

Runoff Coefficient (C) in the Rational Method can be obtained from recommended values in the literature [14,26-28] given the soil type, land cover, slope, and design event size, with higher values for larger design storms than for the smaller storms for any land type. Interestingly, the C values reported by Chow [28] for forest/woodlands based on slopes and return periods are higher than those reported by Singh [14], indicating high variability and uncertainty, possibly also due to surface depression storage and antecedent moisture. Furthermore, surface runoff is rare in forest environments, with a dominance of subsurface flow processes resulting in moderated peak flows [29,30]. We, therefore, suggest that the currently published C values for forests be evaluated using on-site measured rainfall-runoff events covering a wider climatic range for the EFR and other watersheds with various forests for validation and modification, if necessary.

Time of Concentration (tc) is used to select precipitation intensity from the PIDF curve for a duration =tc for a given site PIDF value in the Rational Method as well as in the SCS Graphical Peak Discharge (GPD) method [15] for estimating peak discharge rates. Several methods are available in the literature [14,15,27,28] for estimating tc mostly using the catchment characteristics. However, the method [15], involving computing separate tc for the overland flow and channel flow parts, is used widely in the U.S. Besides C, the calculation of tc is another source of uncertainty in applying the Rational Method for estimating peak discharge rates [29], as computation of tc is also a function of Manning roughness parameter (n) for overland flow generally reported in the literature [14,15,27,28]. The n parameter may also be dependent on forest surface vegetation which may be relatively denser in the growing season than the dormant season besides during post-fire conditions. For example, effects of plant characteristics and the roughness parameters on stream discharge capacity was shown for a coastal EFR watershed [31,32].

We, therefore, suggest possible improvements in currently available methods to compute tc and related published parameters [14,15,27,28] by using observed storm hyetograph and hydrograph data with high resolution spatial data from the EFRs for varying forested conditions. A somewhat similar approach was used by Hayes [26] for 122 storms from eight small basins with a mixed land use in Virginia. Although the authors validated the Rational Method to some degree, they suggested its further validation with observed flood frequency data, as is being done for three EFR sites in a current study by the authors.

This model requires a single CN parameter, characteristics of soil type, land use and AMCs [33] for event Q estimates from ungauged catchments. Many studies show limitations of this method including instability of CN value for different AMC, lack of explicit dependency between the initial abstraction and the AMC. The authors of [22] reported that the SCS-CN method underestimated the measured event Q in a coastal forest (Figure 2a-Santee), consistent with [17] and warranting its modification for forested watersheds. In another study [19] evaluating the modified SCS-CN versions (SME and mSME) [34,35], the authors showed that, compared to the empirical values, the method under- or over-estimated the CNII (average AMC) value for three EFR watersheds (Santee, Coweeta in Figure 1 and 3rd not shown) in Southeastern U.S. (Figure 2b, Coweeta, NC). As expected, the [35] method, with both enhancement in the AMC and lower value of λ (0.05) in initial abstraction than recommended (0.20) consistent with [36], performed slightly better in predicting Q than that the two other methods. A recent study [20], somewhat similar to [35], with an enhancement in surface and subsurface storage AMC yielded good results for computing Q and Qp for a drained forest in North Carolina. However, there is a critical need to conduct additional validation of the modified methods and their parameters with multi-site year data in varying forest types for reducing uncertainties.

Besides the Rational method, the TR55 based GPD method [15] incorporating calculated Q is also frequently used for estimating design Qp for design of transportation and water management infrastructures also in forested watersheds. The GPD method assumes a default value of pond and swamp adjustment factor (Fp=0.72) for 5% swamps. As shown in [19] and another study [33], default Fp=0.72 should not be used for these forested watersheds with high retention capacities. Although much smaller value around 0.10 was obtained by Walega [19], their results showed Fp value varying with precipitation levels for all three watersheds with the large forest cover and a high soil capacity (Figure 2c). Limited data analysis also showed larger differences in ratios of the Qp (SME_m) and Qp (SCS-CN) particularly for lower frequencies which are critical for engineering design and reliability analysis of structures (Figure 2d).

Figure 2: Example results: a) assessment of SCS-CN predicted Q compared to the measured Q for 20 individual runoff events for the Santee watershed [21], b) CN-P relationships by the standard model in the Coweeta watershed [19], c) Fp-P relationships and d) Ratios of Qp using Q from modified (mSME) and SCS-CN in the TR55 GPD method [15] for different storm frequencies in three forest watersheds [19].

These results clearly show that the simple empirical Rational Method is sensitive to changes in their parameters. One approach to improving the method is to calibrate the parameters, however, calibration is not possible for ungauged watersheds [36,37]. In such circumstances, rainfall-runoff models, such as a GIS based spatially distributed Event-Based Approach for Small and Ungauged Basins (EBA4SUB) model based on unit hydrograph theory, can be used to compute the peak discharge rates using the Rational Method [38,39]. Therefore, we suggest validating these engineering hydrology tools and their modified versions and the parameters with long-term hydro-climatic data from the spectrum of EFR watersheds (Figure 1) and other similar forested watersheds [10]. The variability across these sites will also be equally critical for evaluating their impacts on vulnerability and risk assessments of infrastructure on the forested landscape due to climate and land use change and forest disturbance in the 21^st century.

The authors would like to acknowledge Dr. Carl Trettin and Dr. Jim Vose, both at USDA Forest Service Southern Research Station, for their constructive suggestions for improvement of this Opinion article. “The opinions presented in this article are those of the authors and should not be construed to represent any official USDA or U.S. Government determination or policy.”

1. Amatya DM, Skaggs RW, Trettin CC (2009) Advancing the science of forest hydrology: A challenge to agricultural and biological engineers. Resource, pp. 10-11.
2. Sedell J, Sharpe M, Apple DD, Copenhagen M, Furniss M (2000) Water and the forest service. Forest Service, p. 40.
3. Jones JA, Achterman GL, Augustine LA, Creed IF, Ffolliott PF, et al. (2009) Hydrologic effects of a changing forested landscape: challenges for hydrological sciences. Hydrol Proc 23(18): 2699-2704.
4. USDA (2001) Forests: The potential consequences of climate variability and change. A report of the National Forest Assessment Group for the U.S. Global Change Research program. USDA Global Change Program Office, Washington, USA.
5. Amatya DM, Skaggs RW (2011) Long-term hydrology and water quality of a drained pine plantation in North Carolina, USA. Trans of the ASABE 54(6): 2087-2098.
6. Sun G, Lockaby BG (2012) Water quantity and quality at the urban-rural interface. In: Laband DN, Lockaby BG (Eds.), Urban-Rural Interfaces: Linking People and Nature. American Society of Agronomy, Crop Science Society of America, Soil Science Society of America, Madison, Wisconsin, pp. 26-45.
7. Gorman PA, Schneider T (2009) The physical basis for increases in precipitation extremes in simulations of 21^st century climate change. Proceedings of the National Academy of Sciences 106: 14773–14777.
8. Ingram KT, Dow K, Carter L, Anderson J, Sommer EK (2013) Climate of the Southeast United States: variability, change, impacts, and vulnerability. Island Press, USA, p. 358.
9. Amatya DM, Trettin CC (2019) Long-term ecohydrologic monitoring: A case study from santee experimental forest, coastal South Carolina. Submitted, A short communication. Journal of South Carolina Water Resources 6(1): 46-55.
10. Amatya DM, Campbell J, Wohlgemuth P, Elder K, Sebestyen S, et al. (2016) Hydrologic Processes of Reference Watersheds at USDA Forest Service EFRs. In: Amatya DM, TM Williams, et al. (Eds.), Chapter 14, Forest Hydrology: Processes, Management, and Applications, CABI Publishers, UK, pp. 219-239.
11. Vose JM, Swank WT, Adams MB, Amatya DM, Campbell J, et al. (2014) The role of experimental forests and ranges in the development of ecosystem science and biogeochemical cycling research. In: Hayes DC, Stout SL, et al. (Eds.), USDA Forest Service Experimental Forests and Ranges. Springer, New York, USA, pp. 387-403.
12. Creed IF, Spargo AT, Jones JA, Buttle JM, Adams MB, et al. (2014) Changing forest water yields in response to climate warming: results from long-term experimental watershed sites across North America. Global Change Biol 20(10): 3191-3208.
13. Amatya DM, Harrison CA, Trettin CC (2016) Hydro-meteorologic assessment of October 2015 extreme precipitation event on santee experimental forest watersheds, South Carolina. Journal of South Carolina Water Resources 3 (1): 19-30.
14. Singh, VP (2017) Handbook of applied hydrology. In: 2^nd Edition, McGraw Hill, New York, USA.
15. USDA (1986) Urban hydrology for small watersheds. TR-55. United States Department of Agriculture (USDA), Soil Conservation Service, Washington, DC, USA.
16. Kuichling E, Hering R (1889) The relation between the rainfall and the discharge of sewers in populous districts. Transactions of the American Society of Civil Engineers 20(1): 156.
17. Tedela NH, McCutcheon SC, Rasmussen TC, Hawkins PE, Wayne TS, et al. (2012) Runoff curve numbers for 10 small forested watersheds in the mountains of the eastern United States. Journal of Hydrologic Engineering 17(11): 1188-1198.
18. Moran MS, Peters DPC, McClaran MP, Nichols MH, Adams MB (2008) Long-term data collection at USDA experimental sites for studies of ecohydrology. Ecohydrology 1(4): 377-393.
19. Walega A, Amatya DM, Caldwell P, Marion D, Panda S (2020) Assessment of storm direct outflow and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States. Journal of Hydrology: Regional Studies, Volume 27.
20. US DOT (2018) U.S. forest service transportation resiliency guidebook- addressing climate change impacts on U.S. forest service transportation assets. U.S. Department of Transportation John A. Volpe National Transportation Systems Center in Cambridge, Massachusetts, USA.
21. Walega A. Amatya DM (2020) Modification of the SME-CN method for predicting event runoff and peak discharge from a drained forest watershed on North Carolina Atlantic Coastal Plain. Transactions of the ASABE 63(2): 1-15.
22. Wałęga A, Cupak A, Amatya DM, Drożdżal E (2017) Comparison of direct outflow calculated by different methods for mountainous and highland catchments in upper vistula basin, poland and lowland catchment in South Carolina, USA. Acta Sci Pol Formatio Circum 16(1): 187-207.
23. Heredia N, Roper B, Gillespie N, Roghair C (2016) Technical guide for field practitioners: Understanding and monitoring aquatic organism passage at road stream crossings. US Department of Agriculture, Forest Service, National Stream and Aquatic Ecology Center, Technical Report TR-101.
24. Bonnin GM, Martin D, Lin B, Parzybok T, Yekta M, et al. (2006) Precipitation frequency atlas of the United States. NOAA atlas 14(2): 1-65.
25. Perica S, Martin D, Pavlovic S, Roy I, St Laurent M, et al. (2013) NOAA Atlas 14 precipitation-frequency Atlas of the United States. Silver Spring, MD: National Oceanic and Atmospheric Administration.
26. Hayes DC, Young RL (2006) Comparison of peak discharge and runoff characteristic estimates from the rational method to field observations for small basins in central Virginia. Scientific Investigations Report 2005-5254, U.S. Department of Interior, U.S. Geological Survey, Reston, VA, p. 44.
27. McCuen RH (1989) Hydrologic analysis and design. Prentice-Hall Englewood Cliffs, New Jersey, USA.
28. Chow VT, Maidment DR, Mays LW (1988) Applied Hydrology, McGraw Hill, New York, USA.
29. Grimaldi S, Petroselli A (2015) Do we still need the rational formula? An alternative empirical procedure for peak discharge estimation in small and ungauged basins. Hydrological Sciences Journal 60(1): 67-77.
30. Neary D (2016) Long-Term Forest Paired Catchment Studies: What Do They Tell Us That Landscape-Level Monitoring Does Not? MDPI, Forests, 2016, 7, 164.
31. Miroslaw-Swiatek D, Amatya D (2017) Effects of cypress knee roughness on flow resistance and discharge estimates of the Turkey Creek watershed. Ann Warsaw Univ of Life Sci-SGGW, Land Reclam 49(3): 179-199.
32. Miroslaw Swiatek D, Amatya D (2011) Determination of plant characteristics used in discharge capacity assessment of Turkey Creek watershed on South Carolina Coastal Plain, U.S.A. Annals of Warsaw University of Life Sciences, Land Reclamation 43(2): 121-134.
33. Epps TH, Hitchcock DR, Jayakaran AD, Loflin DR, Williams TM, et al. (2013) Curve Number derivation for watersheds draining two headwater streams in lower coastal plain South Carolina, USA. J of Am Wat Res Assoc (JAWRA) 49(6): 1284-1295.
34. Mishra SK, Singh VP (2002) SCS-CN-based hydrologic simulation package. In: Singh VP, Frevert DK (Eds.), Mathematical models in small watershed hydrology and applications. Water Resources Publications, Littleton, pp. 391-464.
35. Sahu RK, Mishra SK, Eldo TI (2012) Performance evaluation of modified versions of SCS curve number method for two catchments of Maharashtra, India. ISH Journal of Hydraulic Engineering 18(1): 27-36.
36. Capece JC, Campbell KL, Baldwin LB (1986) Estimation of runoff peak rates and volume from flatwoods watersheds. University of Florida, Institute of Food and Agriculture Sciences, Gainesville, USA.
37. Bartlett MS, Parolari AJ, McDonnell JJ, Porporato A (2016) Beyond the SCS-CN method: A theoretical framework for spatially lumped rainfall-runoff response. Water Resour Res 52(6): 4608-4627.
38. Petroselli A, Grimaldi S (2018) Design hydrograph estimation in small and fully ungauged basins: a preliminary assessment of the EBA4SUB framework. Journal of Flood Risk Management 11(1): 197-210.
39. Młyński D, Petroselli A, Wałęga A (2018) Flood frequency analysis by an event-based rainfall-runoff model in selected catchments of Southern Poland. Soil and Water Research 13(3): 170-176.