Short Review on Incremental Dynamic Analysis and Fragility Assessment

Introduction

The developments in processing power facilitated the process of modelling by increasing the accuracy of the analysis methods. These developments made it possible to move from elastic static to dynamic elastic and from non-linear static to non-linear dynamic analysis. The latter is based on running several different records separately producing several ‘single-point’ analyses that are mostly used for checking the designed structures. Nowadays, incremental dynamic analysis (IDA) is widely used as a non-linear dynamic analysis method [1-7]. It is a parametric analysis method used to estimate the structural performance under several ground motions and includes the development of one or more curves of a specific damage measure (i.e. drift as a percentage) versus an intensity measure of the ground motion (peak ground acceleration (PGA)).

This method has been studied and discussed comprehensively by several researchers [8,9]. The steps to perform incremental dynamic analysis is summarised as follows:

A. Perform nonlinear analysis of structural building subjected to seismic excitation with certain PGA (i.e. 0.1 g) and record the maximum drift of the structure.

B. Repeat step 1 by increasing the seismic excitation PGA progressively taking an increment (i.e. 0.2g, 0.3g, 0.4g, etc).

C. Continue increasing the PGA until reaching the collapse state.

D. Plot the variation of the Drift as function of the PGA. This is the incremental dynamic analysis curve.

Performing IDA is very useful to study the building response during earthquakes. The main objectives of IDA are [8]:

a. To obtain a deep understanding of the response versus the potential level of ground motion records;

b. To achieve a thorough understanding of the structural behaviour under severe ground motions;

c. To improve understanding on the relation of structural response versus intensity of ground motion (maximum displacement, strength, stiffness);

d. To estimate of the dynamic capacity of the structure

e. To provide better information by studying several ground motions to see how these factors are stable from one ground motion to another.

Selection of earthquake records

The selection of ground motion is one of the most important factors that should be considered in the seismic definition in structural analysis, IDA and the development of fragility curves. Random Selection the ground motions leads to a difficulty in representing the exact variability of the ground motions. The selection of the ground motions has been discussed in detail in [10-12]. Two criteria are given for the selection of ground motion records. The first one considers selecting a record based on previous earthquake events that are widely available in different libraries and websites, such as the Pacific Earthquake Engineering Research (PEER). The second criterion obtains ground motions supplemented by simulations. However, the main drawback of this method is the lack of suitable recordings such as large magnitude ground motions at short site-to-source distances [13]. Owing to this drawback, the first criterion is more widely used than the second. Several aspects should be considered in the process of selecting ground motion records, such as the number of ground motions, the soil type and the properties of the ground motion (i.e. the event magnitude and the peak ground acceleration and the distance between the epicentre of the ground motion and the affected area).

The number of ground motions that should be selected for structural analysis is still a critical issue until now and no agreement has been reached on a specific number by the researchers. Thus, further research is needed to study the effect of the number of ground motions on the behaviour of the structure. However, the codes specify a number that should be used, though the number is different between the codes. Najafi et al. [14] recommended selecting seven ground motions (based on the ASCE05-7 code recommendations) or eleven ground motions (based on the ATC recommendations). The codes UBC 1997, IBC 2000, FEMA-356, EC8, ASCE 2006 and ASCE 2007 recommend three or seven as a minimum number of ground motions to use the mean of the demand parameter in analysing the structure. If the number of ground motions used is less than this recommended number, then the maximum value of the demand parameter should be taken into account for the analysis of the structure.

With regard to other parameters, such as event magnitude, peak ground acceleration, soil type and distance between the epicentre of the ground motion and the affected area, Najafi et al. [14] summarised the process of ground motion selection based on these aspects. They then proposed approach of record selection (step-by-step), determined the primary list of records, chose a representative record for each earthquake event, selected the minimum number of records and explained and performed scaling of the ground motions. Indeed, the effect of the repeated earthquakes was considered by several researchers. This method is based on the combination of two or more artificial single ground motions and scale up to become repeated earthquake specifying a certain time between these two single ground motions. A time gap of 100 s between two consecutive artificial ground motions with zero acceleration is suggested by Hatzigeorgiou [15,16] who found that this duration is sufficient for the structure return to the rest state.

Introduction

The fragility is the probability of the failure of a structure under a specific value of a seismic response parameter, such as maximum acceleration, velocity, displacement, effective acceleration arias intensity and spectral acceleration [9,17]. Several previous studies have presented a historical background of fragility curves [18- 24]. In the majority of the common cases, the seismic response parameter taken into consideration is the PGA so that the objective of the development of fragility curves is to estimate the PGA value where the response of a structure (total structure or certain parts of the structure) reaches or exceeds certain performance level of the structure. Since there are numerous reasons for the structure variability (total structure or certain parts of the structure), fragility is usually expressed by a series of curves. Each curve is characterised by a specific probability value to show uncertainty in the fragility estimation. This specific probability usually corresponds to a specific performance level.

In many research studies, four performance levels have been considered [25]:

A. Operational performance (OP):

The majority of operations and functions can resume immediately, and the structure is still safe for occupancy. The essential operations remain protected and undamaged whereas the non-essential operations disrupted. Repair is required to restore certain non-essential services. Light damage is observed.

B. Immediate occupancy (IO):

The minor structural parts experience considerable damage, but the building gravity or lateral resistance/stiffness is unchanged before and after the earthquake. The damage is expected and includes certain localised yielding and limited fracturing of connections. In this state, the damage may include little localised yielding and limited fracturing of connections.

C. Life safety (LS):

The damage is moderate, but the structure remains stable. The affected structures may be protected from damage and life safety is generally protected. Evacuating the structure is usually required after the earthquake to ensure the safety of people. Repair is possible but economically impractical and expensive due to the high damage occurred.

D. Collapse prevention (CP):

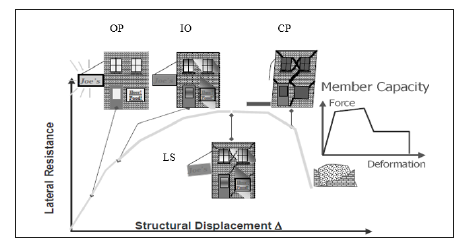
The structure is on the verge of experiencing local or total collapse. It suffers from substantial damage, such as large permanent deformations and considerable degradation in stiffness and strength of the lateral force resisting system. Each performance level is associated with a certain percentage of drift. This percentage depends on the structure type. Figure 1 shows the severity of damage for each performance level and Figure 2 shows the relation between the damage and the demand parameters.

Figure 1:The severity of damage for each performance level [25].

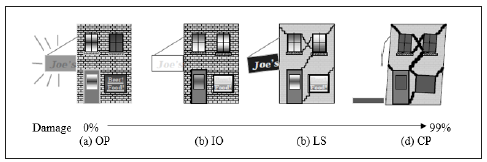
Figure 2:Damage related to demand parameters [25].

Several methods have been used for developing fragility curves, such as expert-based or judgmental, empirical, hybrid and analytical methods that include several equations. The most used method is the analytical method. Analytical methods derive fragility curves from the statistical elaboration of the results of numerical analyses carried out on structural models. For large scale fragility analyses, demand and capacity are usually determined using simplified analytical methods [26-29]. The equation proposed by Ibrahim and El-Shami [30] is considered as the simplest equation:

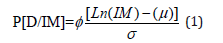
where Φ is the standard normal distribution function, D is the damage state (performance level), IM is the corresponding ground motion Intensity Measure PGA, μ is the mean and σ is the standard deviation of the natural logarithm of PGA at which the building reaches the specific damage state (performance level), D. For instance, if the fragility curve is being plotted for the collapse prevention state, the PGAs that lead to collapse state recorded form IDA is used. Different PGAs are recorded under different ground motions. The natural logarithm of these values is calculated. The mean value and the standard deviation of these values is then estimated and used in Equation 1. This equation has been used by numerous researchers such as Bayati et al. [31] because of its simplicity.

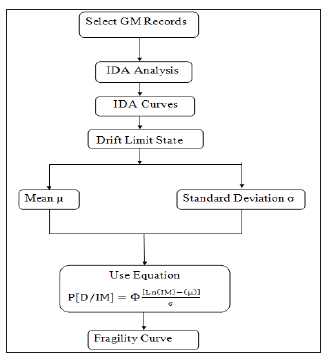
Developing the fragility curves consists of two steps. The first step is to compute the mean and the standard deviation of the collapse capacity using the lognormal Probability Density Function (PDF) of the structural collapse capacity. The second step is to develop the fragility curve using the computed values of mean and standard deviation and the lognormal Cumulative Distribution Function (CDF). Figure 3 shows the general steps for the development of fragility curves.s.

Figure 3:General steps for the development of the fragility curves.

1. Mander JB, Dhakal RP, Mashiko N, Solberg KM (2007) Incremental dynamic analysis applied to seismic financial risk assessment of bridges. Engineering Structures 29(10): 2662-2672.
2. Vejdani HR, Shooshtari A (2008) Comparison of exact IDA and approximate MPA-based IDA for reinforced concrete frames. The 14th World Conference on Earthquake Engineering, Beijing, China, pp.1-8.
3. Tehrani P, Mitchell D (2012) Seismic performance assessment of bridges in Montreal using incremental dynamic analysis. The 15th World Conference on Earthquake Engineering, McGill University, Canada, pp.1- 10.
4. Tehrani P, Mitchell D (2013) Seismic response of bridges subjected to different earthquake types using IDA. Journal of Earthquake Engineering 17(3): 423-448.
5. Alembagheri M, Ghaemian M (2013) Damage assessment of a concrete arch dam through nonlinear incremental dynamic analysis. Soil Dynamics and Earthquake Engineering 44: 127-137.
6. Chomchuen P, Boonyapinyo V(2017) Incremental dynamic analysis with multi-modes for seismic performance evaluation of RC bridges. Engineering Structures 132: 29-43.
7. Rafie NY, Bargi K (2014) Seismic performance assessment of a twospan concrete bridge by applying incremental dynamic analysis. Asian Journal of Civil Engineering 15(1): 1-8.
8. Vamvatsikos D, Cornell CA (2002) Incremental dynamic analysis. Earthquake Engineering & Structural Dynamics 31: 491-514.
9. Kirçil MS, Polat Z (2006) Fragility analysis of mid-rise R/C frame buildings. Engineering Structures 28(9): 1335-1345.
10. Katsanos EI, Sextos AG, Manolis GD (2010) Selection of earthquake ground motion records: A state-of-the-art review from a structural engineering perspective. Soil Dynamics and Earthquake Engineering 30(4): 157-169.
11. Wang G (2011) A ground motion selection and modification method capturing response spectrum characteristics and variability of scenario earthquakes. Soil Dynamics and Earthquake Engineering 31(4): 611- 625
12. Wang G (2011) A ground motion selection and modification method preserving characteristics and aleatory variability of scenario earthquakes,” in Proceeding of the 9th US national and 10th Canadian Conference on Earthquake Engineering, USA, Pp.1-10.
13. Iervolino I, Cornell CA (2005) Record selection for nonlinear seismic analysis of structures. Earthquake Spectra 21(3): 685-713.
14. Najafi LH, Tehranizadeh M (2015) Ground motion selection and scaling in practice. Periodica Polytechnica Civil Engineering 59(2): 233-248.
15. Hatzigeorgiou GD, Liolios AA (2010) Nonlinear behaviour of RC frames under repeated strong ground motions. Soil Dynamics and Earthquake Engineering 30(10): 1010-1025.
16. Hatzivassiliou MP, Hatzigeorgiou GD (2015) Three-dimensional reinforced concrete structures subjected to mainshock-aftershock earthquake sequences,” in 8th GRACM International Congress on Computational Mechanics.
17. Duan X, Pappin JW (2008) A procedure for establishing fragility functions for seismic loss estimate of existing buildings based on nonlinear pushover analysis. The 14th World Conference on Earthquake Engineering, Beijing, China, pp. 1-8.
18. Kumitani S, Takada T (2008) Probabilistic assessment of buildings damage considering aftershocks of earthquakes. The 14th World Conference on Earthquake Engineering, Beijing, China, pp. 1-7.
19. Akkar S, Sucuoğlu H, Yakut A (2005) Displacement-based fragility functions for low-and mid-rise ordinary concrete buildings. Earthquake Spectra 21(4): 901-927.
20. Frankie TM, Gencturk B, Elnashai AS (2012) Simulation-based fragility relationships for unreinforced masonry buildings. Journal of Structural Engineering 139(3): 400-410.
21. Bakhshi A, Asadi P (2013) Probabilistic evaluation of seismic design parameters of RC frames based on fragility curves. Scientia Iranica 20(2): 231-241.
22. Modica A, Stafford PJ (2014) Vector fragility surfaces for reinforced concrete frames in Europe. Bulletin of Earthquake Engineering 12: 1725-1753.
23. Silva V, Crowley H, Varum H, Pinho R, Sousa L (2014) Development of a fragility model for moment-frame RC buildings in Portugal. In: Vulnerability, Uncertainty, and Risk: Quantification, Mitigation and Management, pp. 525-534.
24. Haran PD, Davis R, Sarkar P (2015) Reliability evaluation of RC frame by two major fragility analysis methods. Asian Journal of Civil Engineering 16: 47-66.
25. Basic Concepts: Performance-based Earthquake Engineering. Course: Civeng 227 - Earthquake-Resistant Design, University of California, Berkeley, USA.
26. Calvi GM (1999) A displacement-based approach for vulnerability evaluation of classes of buildings. Journal of Earthquake Engineering 3(3): 411-438.
27. Crowley H, Pinho R, Bommer JJ (2004) A probabilistic displacementbased vulnerability assessment procedure for earthquake loss estimation. Bulletin of Earthquake Engineering 2(2): 173-219.
28. Ordaz M, Miranda E, Reinoso E, Pérez Rocha LE (1998) Seismic loss estimation model for Mexico City. Universidad Nacional Autónoma de México, México.
29. Rota M, Penna A and Strobbia C (2008) Processing Italian damage data to derive typological fragility curves. Soil Dynamics and Earthquake Engineering 28: 933-947.
30. Ibrahim YE and El-Shami MM (2011) Seismic fragility curves for midrise reinforced concrete frames in Kingdom of Saudi Arabia. The IES Journal Part A: Civil & Structural Engineering 4: 213-223.
31. Bayati Z and Mohammadi MS (2012) Ground motion selection and scaling approach for evaluation of reinforced concrete frames against sideway collapse. In 15th World Conference on Earthquake Engineering.