- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Advancements in Civil Engineering & Technology
Elastoplastic Analysis Methods and Capacity Curve Developing Features
Rutman Yu L, Meleshko VA and Ivanov A Yu*
Department of Civil Engineering, Russia
*Corresponding author: Ivanov A Yu, Department of Civil Engineering, Russia
Submission: October 31, 2018;Published: November 09, 2018
Volume2 Issue3september 2018
Abstract
Present-day earthquake engineering practice use to apply for seismic performance evaluation of buildings nonlinear static pushover analysis which is represented by now in various modifications. These modifications consider different analyzing conditions, structural characteristics or depend from some engineer preferences and judgements. But all of these nonlinear static analysis methods implies the capacity (pushover) curve generation for estimation the performance point which characterize the building response due the seismic excitation. For capacity curve developing structural engineers are eligible to use any adequate instrumentation that describes inelastic behavior of a structure in appropriate way. However, the appearance of pushover curve generated by the most commonly used structural analysis software is often not clear enough, contains big number of inflection points, for which reason it could not provide adequate definitive criterion of general structural stability without advanced studying of pushover curve developing methods. In this paper the simplified capacity curve representation method is proposed and it is shown how the capacity curve can be used for financial loss evaluation inflicted by a potential earthquake.
Keywords:Capacity pushover curve; Limit equilibrium state; Elastoplastic analysis; Pseudo-stiffness method; Hybrid finite element method; Spatial rod system; Optimization algorithm by economic criteria; Financial curve
Introduction
Building’s capacity curve developing is generally used in nonlinear static pushover analysis that was developed over the last two decades and became very popular for seismic performance evaluation of building because of its simplicity and ability to consider inelastic behavior. Therefore; the capacity curve developing is closely associated with pushover method researches; the most important was done by Fajfar [1]; Krawinkler & Seneviratna [2]; Chopra & Goel [3]; Gulkan & Sozen [4]. It was introduced capacity spectrum and displacement coefficient methods; which are included in seismic guidelines and provisions [5-7]. Further investigations and studies were aimed to improve and extend the existing theoretical base; specificity of analysis of irregular building was considered by Moghaddam [8]; the influence of inelastic behavior; period elongation and lateral load redistribution was analyzed in [9]; adaptive pushover analysis was proposed in [10]; and its modification was introduced in [11]. All calculations using pushover methods begin from capacity curve construction.
Elastoplastic analysis methods and capacity curve developing features
The premise of capacity curve developing is to show how the gravity load-bearing structure reflects under the gradually increasing lateral load. Obviously; as it is shown in [12]; the solution of this problem implies significant computational efforts for carrying out the inelastic analysis of three-dimensional model of the structure and it is paid the big attention for modelling problems and sensitivity of pushover capacity curve. At the present time; the mainstream computer tool to perform pushover analysis and generate capacity curve is SAP2000; a wide range of studies consider building inelastic behavior simulation problems; especially plastic hinges properties modelling that is the main instrument of nonlinearity consideration in SAP2000 and other structural analysis software which uses direct (classic) elastoplastic analysis approach. This computational method provides the capacity curve with a good accuracy level; the curve contains several points.
Every point corresponds to the certain number of plastic hinges appeared in structural elements at relative step of analysis. Despite the good accuracy of obtained capacity curve; the strength reserve analysis of structures using this direct computational method shows that there is no the unambiguous criterion; which determines explicitly the moment when the structure loses its stability. Also, the main assumption and the disadvantage of the direct method is the fact that the structural engineer have to design self-dependently the scheme of a structure failure; specifying plastic hinges formation zones in elements of the analytical model. In some cases, the actual failure scheme may differ from that specified by the user; which leads to an erroneous prediction of inelastic behavior.
Another way is the simplified method; which; at once; is based on a rigorous assessment of the system limit equilibrium state occurrence and pseudo-stiffness method proposed by Rutman Yu [13]. It is realized in Ing+ MicroFe software suite. This method is based on assumption that the capacity curve can be represented as a bilinear force-displacement approximation with inclined and horizontal region; where the inflection point characterizes the limit equilibrium state. The relative force value can be computed using the limit analysis option by Ing+ and the inclined region slope is determined by providing elastic analysis. This approach allows engineer to save modelling time and to avoid the plastic hinges assignment operation; instead of which it is necessary to define limit elemental forces for structural model elements. As a result of analysis; it is shown automatically by program the amplification coefficient of lateral force at which the structure becomes unstable. It is shown also the plastic deformation zones in structural elements which occur due to this lateral force. Finally; the ultimate roof displacement; which is the end of horizontal region of capacity curve; can be estimated approximately by using the equations proposed in [14]. The merit of this method is low accuracy of the capacity curve which contains only 2 points.
For saving computation time and increasing the accuracy of calculation of rod systems; there is also the hybrid finite element method (hybrid FEM) proposed by Rutman Yu & Meleshko [15-18]; the algorithm of elastoplastic deformations analysis of a spatial rod is suggested in there. Hybrid FEM allows to exclude finite elements from along the rod length and replace it with the integration sites. In [19] the geometric nonlinear model based on the generalized More’s equation with a tangential stiffness matrix is considered. This nonlinear model characterizes the stress distribution through the whole rod section area. The proposed elastoplastic deformation analysis algorithm could be implemented in FEM as a form of deflection or force method. This method allows to obtain a very detailed capacity curve.
Conversion to financial curve
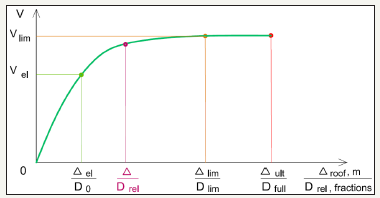
Nowadays; some new optimization algorithms by economic criteria in earthquake engineering appear. Optimization algorithm proposed in [20-22] allows to evaluate the life cycle economic effect by comparing different seismic retrofit schemes of a building at the project design stage. For economic effect estimation it is necessary to know what damage could be inflicted to the structure by any possible seismic excitation on the building site due its life cycle. If the capacity curve is developed; then it becomes possible to evaluate the damage caused by any earthquake. This can be done simply by conversion the MDOF building model to the SDOF system and performing the nonlinear time-history analysis or with the aid of nonlinear static pushover analysis. In the first case the seismic excitation is presented by a time-history; and in the second – by response spectrum obtained from the SDOF system time-history analysis. No matter of the chosen way of computation; the result leads to the target displacement. Taking this target displacement Δ to the capacity curve; the damage state Drel can be evaluated by correlating it with other displacements and their relative damage states; obtained from any elastoplastic analysis described above; and then providing the interpolation. The obtained in such a way curve can be characterized as financial curve (Figure 1).
Figure 1:General configuration of financial curve
Conclusion
In this article several computational methods for providing elastoplastic analysis of structural systems and developing its capacity curve is reviewed. These methods vary according to the accuracy level of analysis results. Through the use different of them; inelastic deformation zones distribution is obtained with desirable accuracy level. Consequently; the damage state can be characterized by larger or smaller points on the curve.
References
- Fajfar P, Krawinkler H (1992) Nonlinear seismic analysis and design of reinforced concrete buildings. Elsevier, London, UK.
- Krawinkler H, Seneviratna (1998) Pros and cons of a pushover analysis of seismic performance evaluation. Journal of Engineering Structures 20(4-6): 452-464.
- Chopra AK, Goel RK (2001) A modal pushover analysis procedure to estimate seismic demands for buildings: theory and preliminary evaluation. Pacific Earthquake Engineering Research Center, College of Engineering University of Berkeley, Berkeley, USA.
- Gulkan P, Sozen MA (1974) Inelastic response of reinforced concrete structures to earthquake ground motions. Journal of the American Concrete Institute 71: 601-609.
- EC8 (2004) Eurocode 8: Design of structures for earthquake resistance. European Committee for Standardisation: Brussels, Belgium, The European Standard EN 1998-1.
- FEMA 356 (2000) Pre-standard and Commentary for the Seismic Rehabilitation of Buildings. ASCE Standards Committee on Seismic Rehabilitation, Washington, DC, USA.
- ATC-40 Report-Applied Technology Council (1996) Seismic evaluation and retrofit of concrete buildings. Redwood City, California, USA 1: 334.
- Moghaddam AS, Tso WK (2000) 3-D pushover analysis for damage assessment of buildings. Journal of Seismology and Earthquake Engineering 2: 23-31.
- Jianmeng M, Changhai Z, C Lili X (2008) An improved modal pushover analysis procedure for estimating seismic demands of structures. Earthquake Engineering and Engineering Vibration 7(1): 25-31.
- Elnashai AS (2001) Advanced inelastic static (pushover) analysis for earthquake applications. Journal of Structural Engineering and Mechanics 12(1): 51-69.
- Antoniou S, Pinho R (2004) Advantages and limitations of adaptive and non-adaptive force-based pushover procedure. Journal of Earthquake Engineering 8(4): 497-522.
- Panandikar N, Narayan BKS (2015) Sensitivity of Pushover Curve to material and geometric modelling-An Analytical investigation.
- Rutman Yu L (1998) Pseudo-stiffness method for the problem of balance limit state of rigid plastic structures. Saint-Petersburg, Russia, p. 53.
- Birbraer AN, Roleder AJ (2009) Extreme actions on structures. Publishing House of the Politechnical University-St. Petersburg, Russia, p. 594.
- Meleshko VA, Rutman Yu L (2015) Strength computation of rod systems with the consideration of physical nonlinearity using the generalized flexibility method GFM. The results are compared with FEM. Eastern European Scientific Journal 6: 150-161.
- Meleshko VA, Rutman Yu L (2017) The generalization of the flexibility method for an elasto-plastic calculation of rod systems. Materials physics and mechanics 31: 67-70.
- Meleshko VA, Rutman Yu L (2017) Generalized flexibility method by the example of plane elastoplastic problem. Procedia structural integrity 6: 140-145.
- Meleshko VA (2017) Generalized force method on the example of plane geometrically nonlinear problem. Procedia structural integrity 6: 115- 121.
- Meleshko VA (2018) Hybrid model for determining the stiffness of a spatial rod with consideration geometric nonlinearity. Journal of Physics: Conf Series.
- Vatin NI, Ivanov A Yu, Rutman Yu L, Chernogorskiy SA (2017) Earthquake engineering optimization of structures by economic criterion. Magazine of Civil Engeneering 8(76): 77-93.
- Ivanov A Yu, Chernogorskiy SA, Vlasov MP (2018) Structural seismic design optimization by economic criteria. Magazine of Civil Engineering 4 (80): 138-150.
- Ivanov A Yu (2018) Optimization of base-isolated structure designs. Vestnik grazhdanskikh inzhenerov-Bulletin of Civil Engineers 4(69): 36- 45.
© 2018 Ivanov A Yu. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version