Modelling Radiation Damping in Rocking Wall Systems

The series of devastating seismic disasters with massive losses in the last decade demonstrate worldwide vulnerability against earthquakes. Days after the March 11, 2011 Sendai, Japan earthquake and tsunami disaster, the President Obama issued a Presidential Policy Directive on National Preparedness on March 30, 2011 to build a resilient US society. Indeed, with growing populations and evermore integrated economies, there is an immediate and extremely critical need for mitigation against earthquakes and other disasters. It is clear from the outcomes of the string of destructive earthquakes in the last few years (China (May 2008) Haiti (January 2010), Chile (March 2010), New Zealand (February 2011), Japan (March 2011), Nepal (April 2015)) that the consequences of such events are wide-reaching and yet, not well understood. The wide-spread destruction, lives lost and displaced, and on-going challenges facing post-disaster recovery efforts have underscored the need for resilient and adaptable buildings and infrastructure which not only can withstand natural hazards, but also can facilitate societal needs post-hazard.

Research efforts towards mitigating the impact of earthquake disasters on structures have highlighted the critical importance of ductility and redundancy in seismic design. Emphasis on ductility in the research and professional engineering communities has grown in the recent years and now motivates most of the current designs approaches to prevent collapse. Research outcomes [1,2] recom mend several preventive design considerations, including providing ductility in elements and connections, and designing to prevent critical structural elements from failure during seismic events. The Performance-Based-Design philosophy places a great emphasis on limiting drift and providing energy dissipation mechanisms to limit damage and reduce the potential for brittle failure. While such preventive measures have been enforced in new construction, the retrofit of existing structures to satisfy the requirements of ductility can prove to be a major financial burden, if not totally unfeasible.

Rocking walls or rocking frames have emerged as an effective structural system that would improve seismic performance while suffering little or no damage during a seismic event [3]. This retrofitting mechanism consists of a stiff shear wall tied to the structure through a series of connecting elements, as shown in Figure 1. The system is designed to transform the structural failure mode from a soft story mechanism caused by column yielding to a less catastrophic beam-yielding scenario, thereby maximizing ductility potential and energy dissipation under seismic loading. The wall is either pinned at its base, or allowed to rock or step on its foundation, a configuration often referred to as a stepped wall. The rocking motion can be a source of seismic energy dissipation and is referred to as radiation damping. To control the rocking motion, however, it is important to provide supplemental energy dissipation mechanisms, often in the form of dry connections, dampers and post-tensioning cables.

Figure 1:Housner [4].

The concept of providing energy dissipation through rocking dates back half a century. Housner first investigated the free vibration response of a rocking block after the great Chilean earthquake of 1960, where it was observed that taller and more slender structures that were able to rock at their foundations survived the earthquake, whereas structures with a fixed base, which were assumed to be more stable, were damaged [4]. Following Housner’s seminal paper numerous studies have been carried out to understand the dynamics of rocking systems [5,6]. Mander and Cheng [7] introduced the Damage Avoidance Design (DAD) philosophy where rocking, structural flexibility and pre-stressing were integrated. Further investigations showed that by adding supplemental energy dissipation, damping devices could enhance the energy dissipation capability of a rocking wall system. Ajrab et al. [8] proposed a six-story rocking wall frame building design with multiple dissipation devices, including pre-stressed tendons and dampers placed strategically to achieve maximum dissipation at locations of large deformations. Later Wada et al. used rocking walls and steel dampers to retrofit an 11-story steel reinforced concrete frame in Japan [9,10]. More recent rocking wall designs incorporated advanced dissipation mechanisms using concentrically braced frames [11,12], buckling restrained frames [13], buckling-restrained braced frames [14] or restorative stabilizing restoring forces as in post-tensioned precast concrete walls [15-17] and moment resisting frame (SC-MRF) building with post-tensioned (PT) connections [18]. Rocking walls have been used effectively in seismic retrofit of existing and historical structures [19] and a number of design configurations have been proposed in the literature and included in seismic design codes and recommendations. Studies showed that rocking wall systems can also greatly improve the seismic performance of offshore platforms [20,21]. However, and although the performance of these systems has been studied and documented in research and practice, some aspects of their behaviour during rocking motion, particularly in the presence of nonlinear deformations in the soil, are still not fully investigated.

Recent trends in the seismic design and analysis of structures have emphasized the importance of soil-structure interaction on structural response to earthquake events. Several studies have shown that the nonlinear response of the soil under seismic loading can lead to significant period elongation and a substantial increase in ductility demands imposed on the superstructure [22]. Research and field observations have also underscored the role of soils such as clay in dissipating seismic energy and reducing the dynamic load applied to the superstructure [22,23]. In rocking wall systems, natural dissipation occurs through inelastic soil behaviour. During rocking motion, each impact of the wall on its base is a source of radiation damping and has significantly impact structural response. For example, while a pinned rocking wall was observed to reduce the concentration of deformations in the foundation and columns of poorly detailed RC buildings, successfully averting a soft-story mechanism, stepped rocking walls have been shown to be more effective in reducing seismic drift. Analysis of a yielding single-degree- of-freedom oscillator attached to a rocking wall reported smaller peak and permanent displacements when coupled with a stepped wall compared to a similar system equipped with a hinged wall. Furthermore, wall weight was observed to factor favorably in the performance of stepped walls, while increasing peak and permanent drift in pinned-wall systems [24,25]. The purpose of this review is to provide a brief overview of available models for radiation damping in rocking wall systems. We discuss models ranging from the early seminal work by Housner [4], to more recent advanced numerical models using finite element analysis. Other sources of passive dissipation such as dampers and post-tensioning cables will not be fully discussed herein.

Modeling radiation damping in rocking walls

The current practice for estimating radiation damping uses an equivalent damping ratio, originally proposed by Housner [4] and developed for a rigid rocking block on rigid soil:

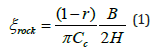
where

ξ_rock = the energy radiated into the half-space per half-cycle (i.e.on each impact)

Cc is the base shear capacity of the wall, and r is the kinetic energy reduction factor/ coefficient of restitution, defined as the ratio between the measured rotational kinetic energy between two cycles:

Using the principal of conservation of angular momentum, the reduction of energy caused by the impact, assuming a rigid wall rocking on a rigid base is calculated as

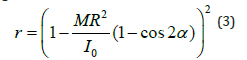
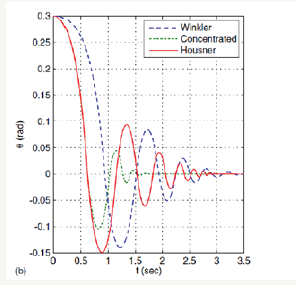
Psycharis and Jennings [26] expanded the Housner model to study the motion of a rigid block rocking on two types of foundations 1) a concentrated model consisting of two spring-damper couples, as shown in Figure 2, and 2) a distributed spring (Winkler)- damper foundation representing distributed soil elasto-plastic behaviour. An alternative definition of the coefficient of restitu tion as the ration of the block velocity before and after impact was used in this approach. Chatzis et al. [27] further expanded this model to consider the effect of tangential sliding, and showed that foundation stiffness and damping characteristics significantly affect the motion of the rocking body, a feature that cannot be captured by Housner’ s rigid base model where the assumption of totally rigid ground results in the dimensions of the body being the parameters that solely define the rocking response [27]. Figure 3 compares histories the rocking motion histories obtained using Housner’ s model with the response calculated with concentrated and distributed elasto-plastic spring models in the soil and shows a clear impact of soil behaviour and Winkler model. While the concentrated model over-estimated rocking-induced seismic dissipation, the distributed elasto-plastic model shows obvious period elongation and amplitude attenuation compared to Housner’s response estimates.

Figure 2:Psycharis et al. [26].

Figure 3:Effect of soil deformability and dissipation on rocking motion [27].

Houbrechts [28] investigated the behavior of a 10-story building resting on a two-dimensional elastic soil domain. A lumped mass model was used for the building and a 2D solid finite elements were used for the soil. Dampers were attached to the soil boundary, with damping coefficients estimated on shear wave velocity for different types of soils. The study demonstrated a great effect of soil properties on radiation damping, with higher energy losses recorded in soft soils [28]. A 2014 experiment conducted at Iowa State University investigated the rocking motion of precast concrete units of various size and shape on a concrete foundation using a nonlinear finite element (FEM) analysis where the soil is modeled explicitly using solid elements and an elasto-plastic constitutive law [29]. Figure 4 compares the FEM angular displacement results with estimates obtained using Houser’s model and experimental results.

Figure 4:Angular displacement response with different foundation models (SRM=Housner’s model).

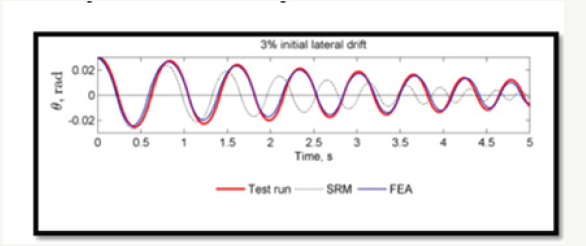
It is evident from this study that even for a concrete base (where rigid base assumption is reasonable) the Housner model cannot adequately capture the response of free rocking members. The FEM results, however, are in good agreement with experimental data. Based on these results, a modified form of Housner’s model is proposed to capture dynamic motion decay in a free rocking structural member on an elasto-plastic foundation. In addition to the effect of soil deformability and plastic dissipation, the above results underscore the importance of capturing contact interactions between the wall and soil along the wall base during rocking. While the Housner model assumes that contact occurs at a single point, often assumed to be the wall’s lower corner, models that have exhibited improved predictions of radiation damping were based on distributed soil modes that can reflect contact along the base surface. A number of researchers have addressed this issue through dedicated contact models for rocking motion. Jafari et al. [30] used nonlinear elastic gap-hook bar elements to model rocking behavior to investigate the effect of axial stress ratio on monolithic self-centering rocking walls.

Kalliontzis et al. [31] proposed improved Coefficient of Restitution values that take into account that finite region over which rocking occurs. Fathi et al. [32] investigated the rocking behavior of high-rise buildings on shallow foundations and different types of geomaterials using a surface-to-surface contact model for the soil-wall interface. An extensive parametric was conducted using a wide range of soil material properties and structural configurations and the results indicated that a significant proportion of the input energy is dissipated through radiation damping especially for the structures on softer geomaterials. However, while calculating the viscous damping in the rocking wall system, researchers adopted the concept of Housner’s Coefficient Of Restitution to simulate and measure rocking decay of motion and equation (3) has been overwhelmingly used till date to calculate the coefficient of restitution (r) [1,2,8], where the impact of soil deformations and material behavior is not explicitly accounted for also the presence of the attached structure is not considered.

The effect of radiation damping on the behavior of rocking wall systems is well documented. Despite the wide-scale availability of computational models for contact and soil constitutive analysis, current practice for estimating radiation damping still relies on the equivalent damping ratio, originally developed by Housner [4] for a rigid rocking block, without accounting for the presence of the structure, and assuming the soil underneath the wall is rigid [8,33,34]. For a high-fidelity analysis of rocking wall systems, it is essential to assess structural response in the presence of sources of nonlinearity in the soil and along the soil-structure interface, including significantly large deformations at variable strain rates, high material nonlinearity and material damage, and partial loss of contact due to uplifting or rocking of the superstructure. FEM model offer the advantage of capturing the effect of nonlinearity of contact between the wall and its foundation.

The authors acknowledge financial support provided by the Purdue Research Foundation.

1. Ellingwood BR, Donald OD (2005) Building design for abnormal loads and progressive collapse. Computer-Aided Civil and Infrastructure Engineering 20(3): 194-205.
2. Mohamed OA (2006) Progressive collapse of structures: Annotated bibliography and comparison of codes and standards. Journal of Performance of Constructed Facilities 20(4): 418-425.
3. Wiebe L, Christopoulos C (2014) Controlled rocking systems for enhanced seismic resilience: State of the art Sustain Dev Crit Infrastruct- Proc. 2014. Int Conf Sustain Dev Crit Infrastruct 905: 496-503
4. Housner GW (1963) The behaviour of inverted pendulum structures during earthquake. Bulletin of the Seismological Society of America 53(2): 403-417.
5. Makris N, Vassiliou MF (2013) Planar rocking response and stability analysis of an array of free-standing columns capped with a freely supported rigid beam. Earthq Eng Struct Dyn 42(3): 431-449.
6. Lu X, Mao Y, Chen Y, Liu J, Zhou Y (2013) New structural system for earthquake resilient design. J Earthq Tsunami 7(3): 1350013.
7. Mander JB, Cheng CT (1997) Seismic resistance of bridge piers based on damage avoidance design. Technical Report NCEER-97-0014.
8. Ajrab JJ, Pekcan G, Mander JB (2004) Rocking wall-frame structures with supplemental tendon systems. J Struct Eng 130(6): 895-903.
9. Wada A, Qu Z, Ito H, Motoyui S, Sakata H, et al. (2010) Seismic retrofit using rocking walls and steel dampers. In Improving the Seismic Performance of Existing Buildings and Other Structures, pp. 1010-1021.
10. Wada A, Qu Z, Motoyui S, Sakata H (2011) Seismic retrofit of existing SRC frames using rocking walls and steel dampers. Frontiers of Structural and Civil Engineering 5(3): 259-266.
11. Barbagallo F, Bosco M, Marino EM, Rossi PP (2017) 11.17: Seismic retrofitting of concentrically braced frames by rocking walls and viscous dampers. ce/papers 1(2-3): 2975-2984.
12. Barbagallo F, Bosco M, Marino EM, Rossi PP (2018) Seismic retrofitting of braced frame buildings by RC rocking walls and viscous dampers. Earthquake Engineering & Structural Dynamics 47(13): 2682-2707.
13. Yooprasertchai E, Hadiwijaya IJ, Warnitchai P (2015) Seismic performance of precast concrete rocking walls with buckling restrained braces. Magazine of Concrete Research 68(9): 462-476.
14. Feng Y, Zhang Z, Chong X, Wu J, Meng S (2018) Elastic displacement spectrum- based design of damage-controlling BRBFs with rocking walls. Journal of Constructional Steel Research 148: 691-706.
15. Nicknam A, Filiatrault A (2012) Seismic design and testing of propped rocking wall systems. In Proceedings of the 15th World Conference on Earthquake Engineering (15WCEE).
16. Musselman E, Fournier M, McAlpine P, Sritharan S (2015) Behavior of unbonded post-tensioning monostrand anchorage systems under short duration, high amplitude cyclical loading. Engineering Structures 104(C): 116-125.
17. Blebo FC, Roke DA (2018) Seismic-resistant self-centering rocking core system with buckling restrained columns. Engineering Structures 173: 372-382.
18. Guan X, Burton H, Moradi S (2018) Seismic performance of a self-centering steel moment frame building: From component-level modeling to economic loss assessment. Journal of Constructional Steel Research 150: 129-140.
19. Belleri A, Passoni C, Marini A, Riva P (2016) Hinged-wall solutions for the structural strengthening of existing RC buildings. In Fib Symposium, Cape Town, South Africa.
20. Han GY, Jiang ZW, Nie LW, Zhang JG (2013) Rationalization of structural stiffness of offshore platform with rocking-wall. Appl Mech Mater 351- 352: 923-926.
21. Zhang JG, Jiang ZW (2014) Study on seismic performance of offshore platform with rocking wall- TMD system. Applied Mechanics and Materials 610: 78-83.
22. Mylonakis G, Gazetas G (2000) Seismic soil structure interaction: Beneficial or Detrimental? Journal of Earthquake Engineering 4(3): 277-301.
23. Mylonakis G, Gazetas G, Nikolaou S, Michaelides O (2000) The Role of Soil on the Collapse of 18 Piers of the Hanshin expressway in the kobe earthquake. Proceedings of 12th World Conference on Earthquake Engineering, New Zealand, p. 1074.
24. Aghagholizadeh M, Makris N (2017) Seismic response of a yielding structure coupled with a Rocking Wall. Journal of Structural Engineering 144(2).
25. Makris N, Aghagholizadeh M (2017) The dynamics of an elastic structure coupled with a rocking wall. Earthquake Engineering and Structural Dynamics 46(6): 945-962.
26. Psycharis IN, Jennings PC (1983) Rocking of slender rigid bodies allowed to uplift. Earthq Eng Struct Dyn 11(1): 57-76.
27. Chatzis MN, Smyth AW (2012) Robust modeling of the rocking problem. J Eng Mech 138(3).
28. Houbrechts, Jeroen JJ (2008) Influence of soil parameters on the motion of rocking walls. MS thesis. Massachussetts Institute of Technology, Cambridge, USA.
29. Kalliontzis D (2014) Dynamic decay of motion of rocking concrete members. MS thesis, Iowa State University, Ames, Iowa, USA.
30. Jafari A, Ghasemi MR, Bengar HA, Hassani B (2018) Seismic performance and damage incurred by monolithic concrete self-centering rocking walls under the effect of axial stress ratio. Bulletin of Earthquake Engineering 16(2): 831-858.
31. Kalliontzis D, Sritharan S, Schultz A (2016) Improved coefficient of restitution estimation for free rocking members. J Struct Eng 142(12).
32. Fathi A, Haeri SM, Palizi M, Mazari, M, Tirado C, et al. (2018) Performance enhancement of soil-structure systems using a controlled rocking. Geophysics, pp. 1-19.
33. Hamid NH, Mander JB (2014) Damage avoidance design for buildings. KSCE J Civ Eng 18(2): 541-548.
34. Hayati N, Hamid A (2010) A concept development and proposed design procedure for rocking precast hollow core. Journal - The Institution of Engineers, Malaysia 71(2): 18-26.