Inhomogeneous Materials and Excited Brain Tissue Require Nonlinear Description

Material science found that homogeneous materials are usually represented by one frequency, while inhomogeneous materials like doped organic polymers are characterized by more than one frequency. The structure becomes inhomogeneous because the organic polymer is semi-conducting and the areas with imperfect structure where the dopant precipitate, are conducting. These islands of conducting dopant, which are imbedded in the semiconducting media of the organic polymer, make the whole material conducting [1]. They also make the material to exhibit hysteresis properties.

Each organ and each tissue specific formation, such as bones, skin, etc. is a homogeneous media because it is built by one specific type of tissue cells. Therefore, each organ must be represented by one frequency: the heart-by heart rate fh, the lungs - by breathing rate fl, and so on. Hence, in living beings just as in material science homogeneous media are represented by one frequency. The brain is characterized by more than one frequency: alpha waves with frequency 8-12 cycles per second (c/s), beta waves with frequency 13-28c/s, theta waves with frequency 3-8c/s, and delta waves [2]. Is the structure of the brain inhomogeneous?

The brain is a semi-conducting gray matter and the neurons, synapses, and glial cells imbedded in it are conductors because they transmit signals through transport of ions. Synapses are the gaps at the junction of two neurons consisting of pre-synaptic and post-synaptic membranes and the nerve signal between them is transmitted by ions and electrically charged neurotransmitters. Neurotransmitters are electrically charged substances, which are synthesized and stored in vesicles at the pre-synaptic membrane, ready to be released when a nerve signal appears. Their transport through the gap together with ions changes the potential of the postsynaptic membrane. Glial cells are nerve-connecting tissues, which could be considered as neuronal pools (neuronal continuum).

Thus, all neuronal formations are conducting, and they are imbedded in the gray matter of the brain, which has semi-conducting properties. This makes the brain inhomogeneous, which means we can expect nonlinear properties, such as hysteresis and more than one characteristic frequency, just as in the case of doped organic polymers [1]. This is exactly what was observed experimentally (see next section). They can be described only with nonlinear equations. Norbert Wigner first developed a theory for nonlinear systems, which is presented in his book Nonlinear Problems of Random Theory [3]. He underlines there that the systems characterized by more than one frequency can be described only by nonlinear equations. Since the brain is inhomogeneous medium, and is characterized by more than one representing frequency, only nonlinear equations should be able to describe it.

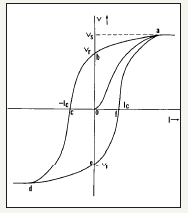
Both living tissues and materials, after certain degree of inhomogeneity exhibit nonlinear properties such as hysteresis. [4,5] was the first to measure volt-ampere characteristics of the brain and find out hysteresis curves (Figure 1). “Hysteresis” means “residual history”. Such materials or tissues react differently to electric or magnetic field, depending on whether the field is increasing or decreasing. This is because the increasing field induces long-lasting changes in the material or tissue. For that reason, when the field is decreased, the material or tissue is found to have slightly different properties, as if it remembers the previous treatment in Figure 1. Long-lasting changes are possible only in systems with long-range correlations, which are specific for farfrom- equilibrium systems described by nonlinear equations [4]. Since the measured hysteresis of the brain result from long-range long-lasting correlations, the brain and its hysteresis would require a nonlinear description.

Figure 1:Tissues react differently to electric or magnetic field.

When a wave propagates in inhomogeneous materials usually it breaks into solitons (=nonlinear waves) and ripples [6,7] found such solitons in the inhomogeneous doped organic polymers and determined their speed from the noise type, low intensity waves in NMR-spectrum of the material. The same can be expected for inhomogeneous tissues such as the brain. We believe that the speed of propagation of solitons in the inhomogeneous brain tissue could be found from the noise type, low intensity brain waves in the magneto-encephalograms (MEG) of the brain, in the way [7] did this in 1988 for inhomogeneous materials.

What is a soliton wave or soliton? The Scottish scientist and engineer John Scott Russell [8] first documented observed by him solitary wave in a canal barge in 1834. He noticed a novel type of stable water wave, which he described in the following way:

A. I was observing the motion of a boat which was rapidly drawn along a narrow channel by a pair of horses, when the boat suddenly stopped-not so the mass of water in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation, then suddenly leaving it behind, rolled forward with great velocity, assuming the form of large solitary elevation, a rounded, smooth and well defined heap of water, which continue its course along the channel apparently without change of form or diminution of speed.

B. I followed it on horseback and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original Figure 1 some thirty feet long and a foot to a foot and a half height. Its height gradually diminished and after a chase of one or two miles I lost it in the windings of the channel [9].

Thus, specific feature of the solitons is their stability. While the normal, linear waves dissipate rapidly, the solitary (nonlinear) waves are very stable. Since the brain is inhomogeneous and exhibits nonlinear properties, nonlinear waves can be expected and in future articles we are going to use a nonlinear mathematical model to describe them.

In the creative state of ecstasy when the subconscious and the conscious work as one whole piece at the same level of overexcitement and the measured brain waves are coherent, we can expect no soliton waves. We hope the information about soliton presence extracted from the low intensity waves of EEG and MEG will confirm this prediction.

1. Kuman NM, Narten AH (1988) Organic polymer conductivity- A nonlinear approach. Synthetic Metals 27(1): A89-A98.
2. Pribram K, Sabourin ME, Cutcomb SD, Crawford HJ (1990) EEG correlates of hypnotic susceptibility and hypnotic trance: spectral analysis and coherence. Int J Psychophysiol 10(2): 125-142.
3. Wigner N (1959) Nonlinear problems of random theory. MIT Press, MIT, Massachusetts, USA.
4. Prigogine I (1984) Order out of chaos. Bantam Books, Toronto, Canada.
5. Adams RN (1986) Annals of the New York Academy of Sciences 473: 42- 91.
6. (1985) Brain Research 40: 151-201.
7. Hirota R, Suzuki K (1973) Proc IEEE. 61: 1483
8. Delrieu JM, Roger M, Coulon C, Laversanne R, Dupart E (1988) Determination of SDW vector and amplitude by NMR and anisotropy by EPR in (TMTTF)2SbF6 and (TMTSF)2ClO4. Synthetic Metals 27(3-4): 35- 40.
9. John SR (1844) Report on waves In: John M (Ed.), 14th Meeting of the British Association for Advancement of Science, London, UK.