Predicting Chronic Diseases in Torus Representation

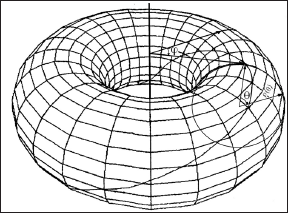
Stressors cause delays because the body needs to stop its work and mobilize for response to the stressors - fight or flight, adapt, or resist. The delays in the body periodic reactions, called biorhythms, are called phase shifts [2]. Since the electromagnetic field of the human body and its organs has the shape of a torus (Figure 1), the equations describing the state of health or disease of the body are maximally simple in torus representation. Also, the torus representation offers geometrical presentation, which gives us the opportunity to see what is going on in a body under stress. In this article, we will show that if we plot in torus representation the curves of phase-shifts-resetting caused by strong or prolonged stress, we can predict the onset of chronic diseases [3,4]. When the external stressors are moderate or weak, they create small delays or phase shifts in the biorhythms, for which the body can compensate. This allows successful adaptation, which in torus representation is presented as resetting of the phase-shift curve from circle to ellipse (Figure 2). When the stressors are strong or prolonged, they create large delays or phase shifts in the biorhythms, for which the body cannot compensate. The critical value, after which compensation is no longer possible, is called the ultimate stress, which the organ can tolerate. When the level of ultimate stress is reached, the body fails to adapt and maladaptation takes place, which leads to chronic disease. In torus representation, it is illustrated as looping of the phase-shift-resetting curve through the hole of the torus (Figure 3)[5].

Figure 1: Heart’s electromagnetic field (adopted from the webpage of the Heart Math Institute).

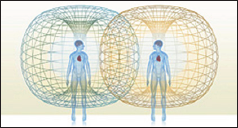
Figure 2: Weak curve resetting representing successful adaptation to weak stressors.

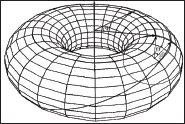
Figure 3: Strong curve resetting (looping through the hole of the torus) representing failure to successfully adapt to strong stressors, which results in maladaptation manifested as chronic disease.

The 40-year work on stress of Hans Selye showed that the same stress causes chronic diseases of different organs in different individuals. In engineering, in the way stress on a material would crack the material at its weakest place, the psychological stress "cracks" the weakest organ. The delays (phase shifts) caused by stress accumulate in the genetically inherited weak organ, which does not have enough energy to propel them. When the ultimate level of stress, which this weak organ can tolerate, is reached, its biorhythms become totally desynchronized. Trying to adapt to the stressors, the organ shifts to a new type of biorhythm order with weaker integration among the biorhythms, which would better tolerate stressors. During prolonged stress: the accumulation of the phase shifts in the genetically inherited weak organ, the desynchronization of its biorhythms, and its evolution to a state with a new type of biorhythm order takes years. This makes the onset of chronic disease slow- usually it takes 5 to 7 years.

The non-equilibrium theory of Prigogine [1] teaches that strong or prolonged force would drag a system to a far-from- equilibrium state. Since each chronic disease results from strong or prolonged stress, each chronic disease must be, and it is, a far-from- equilibrium state. It has a deeper energy minimum than the state of health because some energy has been used to mobilize the body for response to the stressors and some energy has been lost in the biorhythm reordering [5]. Each reordering has chaotic nature and in the non-equilibrium theory of Prigogine [1] it is called dissipative structures. Since every attempt to restore the health or cure a chronic disease requires reordering, which has chaotic nature, the cure of chronic diseases becomes unpredictable in principle [5].

Winfree [4] tried to explain the observed unpredictability and he felt that more measurements were probably necessary. Here is his citation:"After the critical stimulus, the system won't stay at ambiguous phase, but neither is it allowed to have any predictable phase, so it becomes unpredictable. The biochemists wrung their hands over the irreproducibility of their results in certain regions: 'Synchronization does not follow any clear pattern, the reason... is not understood at this time. Much more experimentation is probably needed'" [4]. However, more experimentation will not help because according to the non equilibrium theory of Prigogine [1], if a system is driven very far from equilibrium, beyond a critical point, the events become unpredictable in principle. The points, beyond which the system becomes unstable and the events unpredictable, are called singularity points. The singularity points are also bifurcation points because they give birth to a new solutionin our case the state of pathology called chronic disease [5,6].

Thus, the state of chronic disease is a stable far-from- equilibrium state with deep energetic minimum, which resulted from prolonged stress; it took a series of stressors and time to drag the genetically weak organ of the body to this state of chronic disease. Then it can be expected that the cure, which is leaving this far-from-equilibrium state, will also be difficult and slow. Since the chronic disease resulted from strong or prolonged stress, which drained a lot of energy from the body, and mild stressors stimulate or add energy to the body, it seems natural to look for a series of mild stressors to add back the missing energy to the chronically sick organ. If the mild stressors act through short time intervals, so that their effects can accumulate, a series of mild stressors could pull the chronically sick organ out of the deep energetic minimum called chronic disease and cure the disease [5]. Such mild stressors are acupuncture treatments. A series of daily acupuncture treatments allows accumulation of the stimulation effect of each treatment, which allows the body to be shifted from the stable state of pathology with deep energy minimum, called chronic disease, to the state of health. Indeed, the only presently available cure of chronic diseases is a series of daily acupuncture treatments [7]. But the cure is difficult and slow. Usually a series of daily acupuncture treatments 14 to 20 days in a row are necessary to cure a chronic disease. Clinical observations show that the cure of chronic diseases is not only slow and difficult, it is unpredictable. Practicing acupuncturists know that sometimes, after the series of acupuncture treatments is over, the body drifts again to the state of chronic disease instead of shifting to the state of health. Then the whole series of daily acupuncture treatments needs to be repeated [7].

It was not known why this is so. However, the non-equilibrium theory of Prigogine [1] brings clarity to the subject: since each chronic disease is a far-from-equilibrium stable state [5], the cure of chronic diseases is unpredictable in principle. This means that the acupuncturist shouldn’t be blamed for not doing his job right- the chronic disease was not cured because of the unpredictable cure of chronic diseases. All this means that the non-equilibrium theory of Prigogine [1] can be used to adequately describe the slow onset and the slow, difficult, and unpredictable cure of chronic diseases. Considering the fact that the onset of a chronic disease of an organ is slow ('chronic' means 'slow') and its cure slow, difficult, and unpredictable, we should be looking for ways to prevent the chronic diseases. Monitoring the stress-induced phase-resetting curve of the genetically weak organ can do this. Human phase-shift resetting curves were measured at Harvard University by Dr. Moore et al. [8]. They could be plotted in torus representation and used for prediction of chronic diseases.

Looking at the phase-resetting curve, we should be able to see how close the organ is to becoming chronically sick and interfere to prevent the disease. In ancient time, acupuncture was mainly used for prevention. Pulse diagnostic was used to monitor the phase shifts by sensing the pulse amplitude [7]. When the deviation from norm was detected early, one acupuncture treatment was usually enough to prevent the oncoming chronic disease.

The changes with time in the organ’s function can be described by the evolution equation

where u is a function describing the state of the genetically- inherited weak organ, E is the energy of integration of its biorhythms, and t is the time.

Let us consider the autonomous case when F does not depend directly on t

Then the solution is harmonic with a period T. Let's expand F in a Taylor’s series around the equilibrium point u⁰, and use the substitution

Then the evolution equation (2.1) can be transformed into

The solution of this equation bifurcates when the coefficient abecomes negative. This bifurcation is the critical point, beyond which the adaptation finishes and maladaptation or pathology starts.

Approach 1

Barnsley [9] in his article's section: "Making Differential Equations with Prescribed Attractors" considers the autonomous system u = F (u) with a vector field F : IR³ x c , where C is a circle with radius r=1. u = u(θ, r, z, f) , where is a phase shift ,(0 ≤θ<2π) r-radius (0≤r≤1) , 0 ≤ z < 2 , f-frequency, and the angular frequency ω) = θ' . The Poincare’s section, which is our checkpoint for watching the progress of resetting orbits, is a regular torus in IR³ .

Approach 2

In the autonomous case, the solution is harmonic with a period T_i or frequency f_i. A system characterized by a number of angular frequencies ω₁, ω₂, ω₃,...ω_i is normally described with equations:

i.e. through a Hamiltonian H =H (I,θ) , which is the classical Hamiltonian H(p,q) after a canonical transformation (p,q)→ (i,θ)

Physical Meaning of I and θ :

Each canonical transformation has to preserve the symplectic area for any closed loop in phase space:

Since the angle has no dimension, the new variable I must have the dimension of an action . Thus, I is action and θ_i are angle variables. In the new representation, the energy is no longer divided into kinetic and potential energy. Systems, which can be transformed or represented in form (2.4), are integrable by definition. Each integrable system with L degrees of freedom has L independent constants of motion. In torus representation, the motion of each integrable system can be reduced into a translation on a torus. The motion is:

Generally the motion is multiply periodic, admitting the Fourier expansion

L irreducible circuits characterize each L-dimensional torus. Then the L variables I_i can be associated with the symplectic area of L irreducible circuits on an L-dimensional torus, as long as all possible deformations of a given irreducible loop have the same action (Figure 2).

This condition is indeed satisfied by invariant tori of an integrable system, because all the deformations of an irreducible circuit are obtained by adding to it a reducible loop of zero action. Then we can define the action variables I as

Taken over the j-th irreducible circuit fi on the torus.

It is not difficult to show that the variables canonically conjugated to I are the angles 0. The existence of a function

Follows from the Lagrangian property of the torus

The function S has multiple values because the L-dimensional torus intersects the L-dimensional plane q=const in a discrete number of points within the 2L-dimensional phase space. If we choose S(q,I) as a generating function for the canonical transformation(p,q)- > (I,θ) the transformation will be given by

For an irreducible circuit Ω_i of the torus, the change of the angles θ_j is simply

So, the conjugate angles θ_j' = θ_j are the privileged angular coordinates on the torus [3].

We want to use this to describe the onset of stress-induced diseases. Stress creates phase shifts and phase shifts modulate the amplitude. Hence, the motion of an integrable system should be multiply periodic of the type (2.6).

Let us consider each stressor as a perturbation v that changes the unperturbed Hamiltonian H₀ (I ) by

Then the function that generates the transformation (I,θ) → (I', θ) is also multiply periodic

Since the Hamiltonian is invariant with respect to this transformation, with accuracy up to o(ε²) we should have

Which leads to

The frequencies are dense in phase space. They vary continuously along the tori. The resonant tori is the one for which

Where ω(I) are the resonance frequencies.

We can study the effect of first order perturbation in the neighbourhood of a given resonant torus by considering the periodic orbits as coordinates. (In the case of two degrees of freedom the resonant torus will have frequencies for the unperturbed torus θ=0, and for perturbed one .

Let us go back to our original equations (2.1) or (2.2), which depend on the variable E. The intersection of a given periodic orbit of energy E with the Poincare section is a fixed point of the map:

where Φⁿ = DFⁿ , the fixed points u(E) will be defined everywhere, except at the resonant energies where

At energies E ⁿ_c the family of periodic orbits bifurcates.

According to the non equilibrium theory, a bifurcation point is simply the appearance of a new solution. In our case, the new solution is the state of stress-induced chronic disease, which resulted from strong or prolonged stress when the stress surpassed the critical value E_c, which the biorhythms of the genetically weak organ can tolerate.

In other words, the ultimate phase shift Δθ_c , which the system of biorhythms of the genetically inherited weak organ can withstand without destruction, has been surpassed. When this happens, the existing order of biorhythms cannot be sustained anymore and the system will evolve to a state with a new type of order with a weaker integration among its biorhythms. This would make the functioning of this organ sluggish and the organ would suffer functional (chronic) disease. Leaving the new state of chronic disease is unpredictable because it requires biorhythm reordering, which has chaotic nature and depends strongly on fluctuations and external influences. This makes the shift from the state of disease to the state of health unpredictable, i.e. makes the cure of chronic diseases unpredictable.

When the generating function S has the form S(I,q), the map p <-> q is given by the gradient of the function S(q) according to

Then according to Thom’s theorem of the catastrophic theory, generic singularities are those which are invariant with respect to small changes in S(q)

The classification of singularities depends only on the dimension of the configurational space.

For some integrable systems, the periodic orbits come in families with L or more parameters. In the L-dimensional case, we are talking about folds and cusping lines that join at a cusp point. In the simplest case of one degree of freedom, the turning point is a fold. Folds also appear at higher dimensional configurational spaces. The fold’s dimension is always one less than that of the configurational space. In two-dimensional space they are said to have co-dimension 1. In the case of three-dimensional system, folds will be two-dimensional surfaces. These folds intersect other planes in caustic lines. Since their dimension is two less than the configurational space, they are said to be co-dimension 2. Caustic lines join at a cusp point.

When exposed to stressors, each body mobilizes for response to them with a release from the adrenal glands of neurotransmitters of stress (adrenaline and noradrenalin) and corticoid hormones. The neurotransmitters are "emergency substances" usually stored ready in vesicles at the neurosynaptic junctions and released at emergencies like stressors. They are released as puffs, or quants. The corticoid hormones released from the adrenal glands aim to quickly raise the body energy for fast response to the stressor: fight or flight, adapt or resist. Thus, we can think of the energy added to the system during mobilization as a quant. If during each mobilization reaction an energy quant is added to the body, the mobilization reactions would need a quantum description. In other words, quantum torus would be necessary to describe the organ and body discrete states of energy.

Each organ is characterized by a wave with specific frequency. Let us determine the amplitude A of the wave characterizing the organ state. The canonical transformation is:

where S(q,I) is the generating function.

In semi-classical approximation, I and θ correspond to the quantum variables I and θ with commutators:

I is a constant of motion, which is known exactly. In θ-representation, the wave function

must have a constant amplitude.

Since the probability for a state should be invariant toward changes of variables

According to (2.21) singularities can be expected at or because singularity means instability and instability means large phase shift gradients leading to extremely large amplitude changes (4.4).

Phase resetting curves

There are two types of phase resetting [3]:

A. Weak resetting results from weak stimulus (stressor) to which the body can adapt. A line that links once (odd=1) around the torus as an ellipse (Figure 2) represents weak resetting in torus representation. In our case, weak resetting (new phase=old phase) will correspond to adaptation to weak stressors.

B. Strong resetting results from strong or prolonged stimulus (stressor) to which the body cannot adapt and maladaptation takes place. A line linking through the hole of the torus (Figure 3) represents strong resetting. In our case, strong resetting will correspond to maladaptation, which results in a stress-induced chronic disease or cancer [5].

As said, chronic diseases take place when strong or prolonged stressors had dragged the genetically inherited weak organ to a level of ultimate stress E_cⁿ , which the organ can no longer endure. This is the critical bifurcation point E_cⁿ (19), after which the genetically weak organ will drift to a far-from-equilibrium state with a new type of biorhythm order with weaker integration of the biorhythms. The organ in the new state would adapt to stressors better, but the weak integration of its biorhythms will make its functioning more sluggish, and as a result the organ will suffer chronic disease. Since each state of chronic disease has a new biorhythm order, the cure of each chronic disease would require reordering, which has chaotic nature. This makes the cure of chronic diseases unpredictable, which forces us to look for ways to early detect the chronic disease (for example, by plotting the resetting curves of the phase shifts caused by stress, which this article offered). The next step would be to prevent the chronic disease with one or two acupuncture treatments.

To early detect the onset of a chronic disease caused by strong or prolonged stress, we should measure systematically the phase shift changes, which the stressors cause, and plot the phase resetting curves. If the resetting curves of the phase shifts go around the torus, but do not link through the hole of the torus, we have successful adaptation (Figure 2). According to the theory of non equilibrium processes, this corresponds to a movement to near- to-equilibrium state (NES), which preserves the internal integrity called homeostasis, and as a result the body remains healthy. If the resetting curves of the phase shifts do link through the hole of the torus, we have maladaptation and chronic disease can be expected (Figure 3). According to the theory of non equilibrium processes, this will lead to evolution to a far-from-equilibrium state (FES) with a new type of biorhythm order-a state of functional (chronic) disease. Plotting the resetting curves will be a way to predict the onset of a chronic disease. Human phase-shift resetting curves were measured at Harvard University by Moore et al. [8]. They could be plotted in torus representation and used for prediction of chronic diseases. The phase-shift dynamic will be explicitly mathematically described in another article.

1. Prigogine I (1984) Order out of Chaos. Toronto-NY-London-Sidney, Bantam Books, USA.
2. Luce GG (1970) Biological rhythms in psychiatry and medicine, NIH, Bethesda, USA.
3. Ozorio AAM (1992) Hamiltonian systems: Chaos and quantization. Cambridge-NY-Melbourne-Sydney, Cambridge University Press, India.
4. Winfree A (1987) The timing of biological clocks. Scientific American Library, New York, USA.
5. Kuman M (1993) What everybody needs to know about chronic pain, chronic diseases, and cancer. Health and Happiness Books, re-edited and updated in 2008.
6. Kuman M (1998) Stress as killer, stress as healer. Health and Happiness Books, (2^nd edn), in 2009, USA.
7. Kuman M (1997) Modern aspects of ancient acupuncture. Health and Happiness Books re-edited and updated in 2009.
8. ; Moore EMC, Czeisler CA, Richardson GS (1983) New England Journal of Medicine 309: 469-476.
9. Barnsley M, Stephen GD (1986) Chaotic dynamic and fractals. New York- London-Montreal-Sydney-Tokyo-Toronto, Academic Press, USA, p. 53.