Methodological Remarks on Justice as Fairness in Its Relations with Social and Human Sciences

Justice as fairness is a political theory of justice invented by Rawls J [1,2]. The purpose of this essay is to clarify the theoretical character of justice as fairness by comparing its methodology with those of other sciences, specifically neoclassical economic theory, game theory, and metamathematics. We shall also discuss its relationship with transcendental phenomenology. Examining and comparing these sciences carefully, we will elucidate the scientific character of justice as fairness as a political science. Namely, we will show that justice as fairness is not a list of principles of justice that are proposed as philosophical theses alleged to be rigorous and eternal but rather as a theory that can prove itself via principles as (meta-) theorems, which are open to the possibilities of being corrected, revised, and replaced by more accurate and valid theorems (principles). In other words, justice as fairness is a theory that can grow and evolve in its own methods. This is the precise nature of any healthy theory eligible to be called a science. In this introductory section, we briefly outline each section of the essay.
The first and the most important aspect to be stressed is that we observe a common theoretical structure among all scientific areas, namely that they first construct formal ‘models’ at the object level, in which to work with theoretical (and usually abstract) concepts, run analyses, and obtain formal results. Justice as fairness has original position as its central apparatus, which-as we explain in this essay-corresponds to market models in economic theory [3], normal and extensive game forms in game theory [4,5], social models in social choice theory [6] and Peano arithmetic in metamathematics [7]. In the social sciences, we usually ‘interpret’ (at the meta level) the theoretical results obtained in the models (the object level). This procedure is especially significant in justice as fairness, since the crucial objective for any political theory is to avoid value judgements influencing our conclusions. In Section 2, we examine how Rawls tries to exclude partialities from his original position with his ingenious idea of the veil of ignorance. However, unavoidable value judgements at the meta level would be incorporated into our final conclusions as we interpret the formal results obtained in the original position. We also see that Rawls handles the problem of subjectivity induced by value judgements at the final stage with reflective equilibrium. We focus on the role and fundamental significance of reflective equilibrium by comparing justice as fairness to metamathematics and transcendental phenomenology.
In Section 3, we compare the frameworks of justice as fairness with economic and game theories. The similarity between these theories is direct and manifest. Rawls’s discovery of this connection between political and economic theories most impressively reveals his philosophical ingenuity. However, we should not be misled by the apparent analogy between justice as fairness and economics. We shall show that Rawls’s formulation of basic rights as a primary good would invoke serious theoretical problems and criticisms, and that this comes from a fundamental difference between political and economic theories which Rawls has probably overlooked. Herein we propose an alternative to the basic rights concept, which is both free from these problems and distinctive from the concept of natural rights. Our proposed basic rights concept is based on a careful examination of the differences in the philosophical natures of original position and market model. We also prove a meta theorem of political theory, which asserts that natural rights in the sense of Hart [8] would not exist in justice as fairness. This theorem might be considered quite a strong argument that generally disproves natural rights.
In Section 4, we explore an impressive similarity between justice as fairness and metamathematics through examining the proofs of Gödel’s incompleteness theorems. There we see that justice as fairness might be called a metaethics and that the principles of justice are proved as meta theorems, very similarly to how Gödel’s incompleteness theorems are meta theorems in metamathematics (we provide the proofs of incomplete theorems in the Appendix). However, again, we should not be misled by the similarities between these two fields of science. We discuss the methods of assessing the validity and truthfulness of results in both sciences and see that the raison d’etre for reflective equilibrium consists of its end to ensure the validity of results, which are not required in the case of metamathematics.
In Section 5, we also discuss the relations between justice as fairness and the transcendental phenomenology of E. Husserl from an epistemological perspective. His central concepts of lifeworld and transcendental reduction (epochē), and their relevance to original position and reflective equilibrium are elaborated upon. We appreciate transcendental reduction as a philosophical method of investigation and clarification but criticize transcendental phenomenology for its ignorance of ideologies in the sense of Althusser et al. [9,10]. Consequently, we assert that he did not recognize that political concepts and theories are outside a range of transcendental phenomenology, although Husserl [11] claimed that the phenomenology would be the ultimate and fundamental basis for all philosophies and sciences. This would carry similar implications for other social and human sciences, such as history or anthropology. Through our considerations and elaborations thus far, we assert that justice as fairness is eligible to be considered an independent and freestanding political science. These considerations are finally concluded in section 6.

When one reads A Theory of Justice (hereafter Theory) carefully, one recognizes that it has fundamental postulates, which we refer to as axioms. The first is:

Axiom 1: A society is a cooperative venture for mutual advantage (Theory, 4).
A view of actual societies represented by Axiom 1 is the basis of justice as fairness. We note that it expresses the idea of mutual advantage. This is nothing but reciprocity and plays a key role in Rawls’s philosophy. The second axiom is less obvious:

Axiom 2: No one deserves greater natural capacity, nor merits a more favorable starting place in society. The distribution of natural talents should be regarded as a common asset (ibid., 101-102).
It is important to keep in mind that these axioms are postulated at the meta level, meaning that they apply to everyone (including Rawls). We accept both axioms as our truth, and they require no further justification (hence, axioms). Different axioms would yield different theories. Of course, the goal of justice as fairness is described by the two principles of justice.

The First Principle: Each person is to have an equal right to the most extensive basic liberty compatible with a similar liberty for others (ibid., 60).

The Second Principle: Social and economic inequalities are to be arranged so that they are both.
1. attached to positions and offices open to all, and
2. to the greatest benefit of the least advantaged (ibid., 83).
Rawls emphasized that the first principle is more fundamental than the second principle, and its priority is absolute: These principles the two principles are to be arranged in a serial order, with the first principle prior to the second. This ordering means that a departure from the institutions of equal liberty required by the first principle cannot be justified by, or compensated for, greater social and economic advantages (ibid., 61). A successful theory of justice is nothing but a whole body of arguments from which the two principles from the two axioms may be deduced in the most continuous and smooth manner possible. Rawls’s fundamental idea on achieving is as follows. First, he sets the original position whereby free and rational persons (moral agents) face a set of alternative principles. In the Theory, the alternative is the utilitarian principle which consists of the first principle.

The Principle of Restricted Utility: The basic social institution should be organized so that average utility is maximized under the constraint that a certain social minimum is maintained.
They choose a (set of) principle(s) to maximize the (index of) primary goods, which include basic rights, liberties, wealth, and selfrespect. Their decision is made behind a veil of ignorance which is an assumption that they do not know how the various alternatives will affect their own case and they are obliged to evaluate principles solely based on general considerations (ibid., 136-137). Rawls concludes that they choose the two principles rather than the utilitarian principle which orders them to maximize the total utility of the society if their decision follows the maximin criterion. The maximin criterion is the method for choosing alternatives (strategies) based on the worst outcome chosen being superior to the worst outcomes of the alternatives. For example, in Table 1, each number represents a payoff obtained from the corresponding alternative/circumstance pair. The maximin rule requires us to choose A3. It is intuitively obvious why the two principles are chosen rather than the utilitarian principle under this criterion. By the veil of ignorance, people in the original position do not know their own circumstances in their actual societies, hence they might be in the position of the least advantaged. While the difference principle states that socioeconomic inequalities are to be arranged to the greatest benefit of the least advantaged, hence the difference principle cares the least advantaged, the utilitarian principle does not.

Table 1:

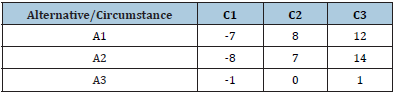
Rawls claimed that the deducting procedure and results (the two principles) of justice as fairness should be confirmed by checking whether they are supported as reflective equilibrium: We can check an interpretation of the initial situation original position, then, by the capacity of its principles to accommodate our firmest convictions and to provide guidance where guidance is needed. In searching for the most favored description of this situation, we work from both ends. We begin by describing it so that it represents generally shared and preferably weak conditions. We then see if these principles are strong enough to yield a significant set of principles. If not, we look for further premises equally reasonable. But if so, and these principles match our considered convictions of justice, then so far so good. But presumably there will be discrepancies. In this case we have a choice. We can either modify the accounts of the initial situation or we can revise our existing judgements, for even the judgements we take provisionary as fixed points are liable to revision. By going back and forth, sometimes altering the conditions of the contractual circumstances, at others withdrawing our judgements and conforming them to principles, I assume that eventually we shall find a description of the initial situation that both expresses reasonable conditions and yields principles which match our considered judgments duly pruned and adjusted. This situation I refer to as reflective equilibrium (Theory, 20).
Although we may not be able to say that Rawls’s expositions on reflective equilibrium are perfectly clear, we discuss its fundamental character and significance for justice as fairness in the subsequent sections. Once the parties in the original position have selected the two principles of justice, they move on to a constitutional convention and create their constitution subject to the principles which they have adopted. Here the veil of ignorance is partially lifted, and the parties obtain sufficient information to determine the constitution. After that, they move forward to the legislative stage and the veil of ignorance is further lifted. The last stage is the application of laws to individual cases by judges and administrators. The participants are now citizens who obey the established rules of their society. The veil of ignorance is now gone, and everyone has full access to all facts. Justice as fairness is completed by this four-stage sequence.

The methodological transfer from economic and game theories to justice as fairness is manifest and evident. Indeed, the idea of veil of ignorance makes the decision-making process of participants in the original position very similar to the behaviors of economic agents or game players under conditions of uncertainty. This probably reveals Rawls’s originality most brilliantly. We notice that the concept of primary goods plays a key role here. However, Arrow [12] and Hart [13] simultaneously questioned the consistency between the priority of the first principle and the assumption that primary goods include basic rights and liberties. From an economic theory perspective, they seem to be compatible only when people have extremely strong preferences, such as for lexicographic ordering, over basic rights, and liberties. How can such a strong preference be justified? Rawls [14] tried to answer this serious question, but it seems fair to assert that he failed in providing an entirely convincing answer. Moreover, Harsanyi [15] severely criticized the use of the maximin rule, which he described as irrationally risk averse and unable to be justified as a manner of decision-making under conditions of uncertainty. He claimed that maximizing the expected utility is the more correct criterion to be used here. These questions and criticisms suggest that the concept of primary goods and the assumption that people maximize the index of primary goods, although they allow Rawls to apply the machineries of economics and game theory ingeniously, required reconsideration.
Concerning the primary goods, we have one additional question about the basic rights and liberties as items of the primary goods. Fundamentally speaking, it seems difficult to understand the basic rights and liberties as ‘goods (items of commodity bundle).’ When we mention ‘obtaining’ or ‘allocating’ those rights and liberties, we suppose that the terms are used in a metaphorical sense at best. If one takes the concept of rights and liberties as goods literally, the question by Arrow and Hart ‘why one or two particular ‘goods’ are so special and distinguished from any other goods?’ is unavoidable. We would like to support Rawls’s claim that the first principle concerning the basic rights and liberties has absolute priority over the second; we do so not because the rights and liberties are especially important among other primary goods, but because they are basic constituents of liberal societies. These concepts are not on the same level as other primary goods. We propose the following definition: The ‘right’ stated in the first principle is a membership (license) authorized by society. In that case, the first principal postulates (very roughly) that it is a right to the most extensive basic liberty compatible with a similar liberty for others. As a membership license, it entitles and qualifies people to pursue their life plans freely if (and only if) they are compatible with those of others. The fundamental intuition behind this definition is that the concept of rights does not express any kind of ‘entities’ or ‘attributes,’ such as the moral or legal characteristics of persons. It goes without saying that rights are not any kind of ‘things’ or ‘goods.’ Rather, it expresses a ‘relationship’ among citizens. Hence it is a common expression that ‘we have a right such that’ the precise meaning of should be ‘we exist (or live) in a social relationship expressed by such a kind of right that’ Moreover, it should be emphasized that the rights defined by membership in a society will be meaningless for a person who is isolated from that society. It is meaningful only within society. Therefore, it is not a natural right. Let us examine this point more closely. First, what are natural rights? Hart’s [8] modern definition states that natural rights are characterized by two properties (ibid., 175):
1. The citizens have the natural right qua men and not only if they are members of some society or stand in some special relation to each other.
2. This right is not created or conferred by men’s voluntary action.
We can now prove the next theorem.
Theorem: There exist no natural rights in justice as fairness. Proof: If the natural rights existed in justice as fairness, they must exist in the original position, otherwise by the condition (2) they would not exist in any subsequent stages of the four-stage sequence. Suppose an original position in which there exists only one person. In such a society, she would be able to do everything she wanted; in other words, she has a ‘right’ to do everything she wants to do. Obviously, this means that the concept of ‘rights,’ whatever they are meant to be, lose their meaning. Indeed, right as a form of membership would make no sense, but according to the condition (1), natural rights claim that they keep their meaning (otherwise they are not natural rights). This is a contradiction. Hence there exists no such concept as natural rights in justice as fairness. QED. Now we shall elaborate on the scientific natures of neoclassical market theory and justice as fairness. What are their common properties and what are the differences between these sciences? We also want to make clear the theoretical status of this theorem. The fundamentally common character of both theories is that they set up theoretical models at the beginning of the analysis. They are nothing but devices of representation; thus, they are not descriptions of realities. Some terms such as ‘(fundamental) rights’ or ‘(market) prices’ are used both in the models and the real world. However, when these terms are used in the models, they are theoretical concepts that are philosophically different from ordinary words. The theoretical concepts are ‘formally’ or perhaps ‘transcendentally’ reduced in the sense of Husserl [11]. The terms are common as words between the models and the realities, but they are different epistemologically. The difference would be ‘transcendental’ in the sense of Derrida [16,17]. We will discuss the relationship between justice as fairness and transcendental phenomenology further in Section 5.
The above theorem asserting nonexistence of natural rights is a proposition which holds for relationship of abstract (‘reduced’) concepts. It states nothing about facts directly in any sense of the word. It is a meta-theorem in this sense. We can prove theorems, if any, only for such abstract concepts as meta-theorems, and when we extract from those (meta)theorems any implications for our practices in the actual world, we would do so under some ‘interpretations’ of the models. Usually rules for interpretation are implicit and there is common consensus for them among researchers in the field. Until now, the reflective equilibrium in justice as fairness is nearly the only rule which states explicitly that we should interpret theoretical results from the perspective of our reality. It would be now clear that almost all grievances against market models or original position, such as that they are ‘unrealistic’ or ‘too abstract,’ are off the mark. They miss the crucial difference between those models and realities as explained above. We will look at this point more closely in the next section. Next, we shall discuss a distinction of economics and justice as fairness. There seems to be an obvious analogy between a natural right endowed to a moral agent of justice as fairness and a characteristic such as a utility function endowed to a consumer in microeconomics. However, this analogy is rather superficial and restrictive. This will be apparent if one realizes that markets with only one consumer make theoretical sense (indeed, such a market model is the subject of optimal growth theory), while original positions with only one moral agent do not, as shown in our proof above. The reason for this is that theoretical concepts in microeconomic theory are constituted by the relationships between economic agents and commodities. On the one hand, the utility functions specify the agent to whom the utility belongs and are defined based on the consumption set (the domain of the utility function), which is a subset of the commodity space. Markets with only consumers (and no commodities) or with only commodities (and no consumers) would be nonsense! On the other hand, the concepts in justice as fairness are constituted only by the relationships among moral agents. A single agent cannot form ‘relationships.’ In such an original position, she could choose whatever she wanted, and any principles of justice, say the utilitarian or libertarian principles (e.g., [18]), would be reduced to the same principle, which means that there would be no questions of justice. For moral agents to be well defined, their theoretical description must be complete, or it must be complete even if the agents are isolated from society and placed in a situation where rights play no role. Therefore, natural rights endowed to moral agents are meaningless as their moral characteristics. It is likely that the only moral characteristics that can be meaningfully assumed are intellectual properties and knowledge. In fact, we can imagine a person with some knowledge and intelligence living alone, but not a person living alone with any meaningful rights. For justice as fairness, the concept of rights must be constructed and explained within the theory, not postulated, and given from outside the theory. It is now clear why there is no room for natural rights in justice as fairness, and that these are strong arguments toward disproving the concept of natural rights in general.

In the previous section, we warned that an apparent similarity between justice as fairness and economic and game theories might be misleading in some respects. However, it can also be asserted that the analogy between Rawls’s logic of deduction (of the two principles) and metamathematics is still impressive. Rawls himself was aware of a connection between justice as fairness and metamathematics:
Note, for example, the extraordinary deepening of our understanding of the meaning and justification of statements in logic and mathematics made possible by developments since Frege and Cantor. Knowledge about the fundamental structures of logic and set theory, and their relations to mathematics, has transformed the philosophy of these subjects in a way that conceptual analysis and linguistic investigations never could. One has only to observe the effect of the division of theories into those which are decidable and complete, undecidable yet complete, and neither complete nor decidable. The problem of meaning and truth in logic and mathematics is profoundly altered by the discovery of logical systems illustrating these concepts. Once the substantive content of moral conceptions is better understood, a similar transformation may occur. It is possible that convincing answers to questions of the meaning and justification of moral judgements can be found in no other ways (Theory, 51-2). An outline of the similarities between these theories can be seen in Rosser’s illuminating illustration of the theorems of Gödel and Church: In any proof of Gödel’s theorem or Church’s theorem, two logics (languages) are concerned. One serves as the ‘logic of ordinary discourse’ in which the proof is carried out, and other is a formal logic L, about which the theorem is proved [19].
In justice as fairness, the original position corresponds to the formal system of metamathematics. Rawls proves a proposition in that people in the original position (not us) will select two principles as the best (most desirable). We interpret this proposition to mean ‘the two principles are just’ in our ordinary language at the meta level. In this sense, justice as fairness is a meta-ethic and the two principles are proved as metaethical theorems. We stress here that in the previous section, we have indeed proved a metatheorem which asserts the nonexistence of natural rights in justice as fairness. Recall in Section 3, we stated that some terms such as ‘(fundamental) rights’ or ‘(market) prices’ are both used in the models and the real world which are different ‘transcendentally’. In metamathematics, some of the terms such as ‘axioms,’ ‘meaningful formulae,’ ‘proofs,’ and ‘provable formulae’ are used in both Peano arithmetic and our ordinary mathematical practices in the actual world. As Derrida [16] said, ‘mathematical concepts are ideal. Their beings are thoroughly transparent and exhausted by their phenomenality.’ In other words, arithmetical (mathematical) concepts have been already ‘formally reduced’ from the outset. Metamathematics now reduces them ‘transcendentally’ as metamathematical concepts in Peano arithmetic (a formal system). However, there are no differences between formal systems and actual mathematics in any naïve senses; their difference is again ‘transcendental.’ Let us now examine the procedures of justice as fairness and metamathematics more closely as an example of Gödel’s incompleteness theorems, which assert the existence of undecidable propositions, and unprovability of its consistency in Peano arithmetic (the proofs of incompleteness theorems are given in the Appendix). We then recognize that the fundamental role of Peano arithmetic in Gödel’s theorems is parallel with that of original position in justice as fairness. The essential point of the proofs of these meta-theorems is that a metamathematical question such as: ‘Does there exist some undecidable proposition in ?’ is expressed and solved as an (ordinary) arithmetical question such as: ‘Does there exist some number satisfying such and such conditions?
A metamathematical problem was translated into an (ordinary) number theory problem. We stress that the recursive functions are a crucial and indispensable device for this procedure. Note that they are (ordinary) arithmetical functions at the meta level, hence they are not metamathematical concepts. They are handled at the meta level as well as our own ordinary language, to analyze and solve metamathematical problems in formal systems which are formulated as arithmetical problems at the meta level. Since all mathematical concepts have already been formally reduced, they have no ‘meanings’ at the meta level, i.e., they only have their ‘functions.’ Therefore, we do not know ‘what the propositions or proofs mean’ at the meta level; we do not even know ‘what they are.’ To give their precise ‘meanings,’ we need to define them meta mathematically in formal systems in which they are just strings of mathematical (logical) symbols with certain required conditions.
Similarly, we do not know exactly ‘what justice for liberal societies is’ at the meta level. We only have a vague ‘sense’ of our justice. We set up the original position and transform a problem of political philosophy at the meta level to a problem of decision making under conditions of uncertainty in the original position. We examine the results obtained in original position, interpret them, and conclude about our own justice. Justice as fairness in this sense might be called a kind of meta-ethics or meta-(political) philosophy. While the similarity between those two procedures is obvious, they also have significant differences. In metamathematics, we do not doubt the validity of any arithmetical (mathematical) concepts or our own ordinary practices in mathematics at the meta level. We are confident in using recursive functions in the proof of the (first) incompleteness theorem. Moreover, mathematical inference does not involve any value judgements. Because there are no ‘real’ differences between the arithmetic at the meta level and the Peano arithmetic at the object-level, the results obtained formally in the latter can be interpreted ‘naturally,’ and they say ‘directly’ something true and important about ‘actual’ mathematics.
This is not the case for justice as fairness. For instance, the two axioms involve value and moral judgements which are far from nonproblematic. The priority of basic liberties and rights in primary goods and maximin criterion have invited various criticisms, as described in Section 3. Because philosophical concepts are not mathematically rigorous and inference processes of philosophical discussions are executed by ordinary language, many ambiguities are necessarily involved. Obviously, something is needed in this process to ensure the validity and truthfulness of results which is not required in metamathematics. This is nothing but the reflective equilibrium, and we now understand the reason it is crucial for justice as fairness. To understand its epistemological nature, however, we need to consider it from a philosophically appropriate perspective, namely transcendental phenomenology.

In the Crisis of European Sciences and Transcendental Phenomenology (hereafter Crisis), E. Husserl proposed a fundamental concept of the lifeworld. Precisely speaking, however, it is doubtful that we can call it a ‘concept,’ since according to Husserl: It is pre-given to us all quite naturally, as persons within the horizon of our fellow men, i.e., in every actual connection with others, as ‘the’ world common to us all (Crisis, 122).
In short, the lifeworld is nothing but the actual world in which all natural, social, and human phenomena take place; hence we can identify it with our concept in this essay at the meta level. Husserl claimed definitively that all sciences have their epistemological grounds and the ontic meanings essentially on the lifeworld: The lifeworld is a realm of original self-evidence. One must fully clarify, i.e., bring to ultimate self-evidence, how all the self-evidence of objective-logical accomplishments, through which objective theory (thus mathematical and natural-scientific theory) is grounded in respect of form and content, has its hidden sources of grounding in the ultimately accomplishing life, the life in which the self-evident givenness of the lifeworld forever has, has attained, and attains anew its prescientific ontic meaning (ibid., 127-8).
Although mathematicians and scientists might not agree that ‘mathematical and natural-scientific theory has its hidden sources of grounding in the life-world,’ political philosophers must take this thesis seriously, otherwise where can they look for the ‘sources of grounding’ of their science? The complete understanding (‘one must fully clarify’) of this thesis is the task of transcendental phenomenology. Husserl’s method to achieve this task is the celebrated transcendental reduction (epochē): Clearly required before everything else is the epochē (suspending judgements) in respect to all objective sciences. This means not merely an abstraction from them, such as an imaginary transformation, in thought, of present human experience, such that no science appeared in the picture. What is meant is rather an epochē of all participation in the cognitions of the objective sciences, an epochē of any critical position-taking which is interested in their truth or falsify, even any position on their guiding idea of an objective knowledge of the word (ibid., 135).
Transcendental phenomenology executes the epochē universally and completely in the lifeworld. By doing so, the lifeworld itself would be a scientific object to be explored for transcendental phenomenology (cf. Crisis, §34). No ‘devices of representation’ other than epochē are found here.7 For justice as fairness, the philosophical procedure like the transcendental reduction is more modest, namely that we set up a device of representation (original position) and the reduction of our political thinking in the lifeworld (meta level) is made into it. In the original position, we put our own moral judgements into ‘brackets,’ and fulfill a sort of epochē within the original position. Hence this ‘reduction’ is in a restricted sense. It is not ‘universal’ or ‘complete,’ thus should probably not be called phenomenological reduction. Nevertheless, justice as fairness must contain this procedure of a (restricted) reduction. Why? Husserl claims that ‘the life-world is a realm of original self-evidence.’ It might be so for mathematics and natural sciences, including psychology. In Husserl’s mind, these are the only sciences. For political sciences, however, the lifeworld (meta level) is a realm of ideologies and prejudices which are far from ‘original self-evidence.’ We expect that those ideological concepts such as liberties, rights, and so on, in the lifeworld are formally reduced to abstract and theoretical concepts in the original position. ‘They would be now ideal. Their beings are thoroughly transparent and exhausted by their phenomenality,’10 and obtain some objective propositions.11 This is where transcendental phenomenology can help justice as fairness.
Husserl would admit that the lifeworld is full of ideologies when we live there in ‘the naïve and natural straightforward attitude’ (cf. Crisis, §38). He would claim that they can be phenomenologically reduced within the lifeworld. He would do so by ‘an epochē of any critical position-taking which is interested in their truth or falsify, even any position on their guiding idea of an objective knowledge of the word,’ and consequently any political or moral concepts and propositions are now ‘phenomena’ for us as ‘transcendental subjects.’ What does this mean? It means that they now ‘mean’ nothing, or they have lost their contents and melted down as ideological entities and, as such, leave nothing in our hands. The historical traditions of economics and political theories tells us that the only way to consider those political (ideological) concepts objectively and obtain any meaningful propositions is to construct them as theoretical ideas with the help of devices of representations (theoretical models).
According to Husserl, ‘the epochē of all participation in the cognitions of the objective sciences’ is just a first step: It by no means suffices. In carrying out this epochē, we obviously continue to stand on the ground of the world; it is now reduced to the lifeworld which is valid for us pre-scientifically; it is just that we may use no sort of knowledge arising from the sciences as premises, and we may take the sciences into consideration only as historical facts, taking no position of our own on their truth (ibid., 147). Husserl’s trust for the lifeworld as a basis of the fundamental (‘prescientific’) validity is sound and solid. He requires the same attitude of researchers of history and anthropology: The same holds even if we take as our subject of investigation, in the unity of a systematic survey, all [historical] periods and peoples and finally the entire spatiotemporal world, paying constant attention to the relativity of the surrounding life-worlds of human beings, peoples, and periods as mere matters of fact. The same thing is true of this world survey, in the form of an iterated synthesis of relative, spatio-temporal lifeworld, that is true of a survey lifeworld individually. It is taken one part at a time and then, at a higher level, one surrounding world, one temporal period, at a time: each intuition (yields) an ontic validity, whether in the mode of actuality or possibility. As each intuition occurs, it presupposes others having objective validity -presupposes for us, the observers, the general ground of the validity of the world (ibid., 147).
He seems to believe in the ability of transcendental phenomenology, armored with the epochē, to investigate and solve the problems of those human sciences. We wonder whether he was correct about history and anthropology for the same reasons he was correct about political science, as explained thus far. Since we cannot completely reduce political concepts as we can in metamathematics, the original position cannot be formulated mathematically, and we need an extra process at the meta level to justify the theoretical results obtained at the object level. Reflective equilibrium, or whatever is used for this verification procedure, would be unable to provide absolute evidence for the truth because our ‘considered judgments’ (see Rawls’s exposition for reflective equilibrium cited above) are not just matters of logic or mathematics. They depend heavily upon our historical experiences, knowledge, and information at the meta level (the life world). One would usually take this negatively, and see it as indicating insufficient credibility of a political theory compared with mathematics or other exact sciences. However, we can also look at this aspect of justice as fairness from a positive perspective, if we trust reflective equilibrium to be reasonable, if not exact. That reflective equilibrium does not confirm the two principles of justice with complete certainty means that it is open to the possibility that the two principles might be replaced by ‘better’ principle(s) in the future. This does not mean that the two principles would become wrong, but rather that more accurate principle(s) would be discovered through examinations and exploitations of the two principles, such as more general (‘better’ in this sense) mathematical theorems, or more exact and wide-ranging laws of nature, are discovered in mathematics and physics. In any case, this is a normal phenomenon which occurs in any healthy science and means that justice as fairness is a science which can grow and evolve.

In this essay, we have shown that justice as fairness is eligible to be called a theory of political science as well as political philosophy. As Rawls [1] stressed, justice as fairness is concerned with justice of basic structure of society rather than with institutions of society or actions of individuals. Therefore, whatever justice as fairness proposes to our actual society would be something abstract and general. For instance, the two principles of justice are considered to represent a sort of social end or ideal. As a proposal of science, however, that social ideal would not be a vacuous one such as, say, ideals stemming from humanism ideology which would never be supported by reflective equilibrium, and hence excluded from the theory. As a science, justice as fairness is a theory which follows the same methods and procedures of other sciences including mathematics, contrary to the Husserlian style of apriorism: A theory of justice is subject to the same rules of method as other theories. Definitions and analyses of meaning do not have a special place: definition is but one device used in setting up the general structure of theory. Once the whole framework is worked out, definitions have no distinct status and stand or fall with theory itself (Theory, 50). Obviously, Rawls does not believe that the moral, political, and philosophical concepts can be elaborated or clarified within the lifeworld by any sort of philosophical methods such as ‘reduction,’ or whatever else which allege to reveal their ‘hidden sources of grounding’ in the lifeworld. Rather, he believes that those concepts must be given by definitions and that workable theories must be constructed on the object level. They are mere ‘devices’ for analysis which are necessarily required to be exploited, corrected, and revised. This is exactly what we have seen in this essay. To be corrected and revised intrinsically, however, any scientific theory should reveal its own limitations, weaknesses, and defects. Such a theory must be exact to the highest degree, i.e., any premises should be made explicit in its axioms and results should be stated systematically. Processes of theoretical deduction should be rigorous as much as possible, if not as perfectly rigorous as mathematics. Justice as fairness is now on its way to fulfilling these scientific qualifications. Rawls also addresses how the British tradition of moral science has taken the same attitude toward constructing their theories and declares decisively to follow this tradition: In any case, it is obviously impossible to develop a substantive theory of justice founded solely on truths of logic and definition. The analysis of moral concepts and the a priori, however traditionally understood, is too slender a basis. Moral philosophy must be free to use contingent assumptions and general facts as it pleases. There is no other way to give an account of our considered judgements in reflective equilibrium. This is the conception of the subject adopted by most classical British writers through Sidgwick. I see no reason to depart from it (Theory, 51). We believe that with him, we too should follow this tradition.
Appendix: Proofs of Incomplete Theorems
In this appendix, we sketch proofs of the incomplete theorems following an unpublished note of Gödel [20] for non-specialists. No technically detailed knowledges on meta-mathematics or mathematical logic are presupposed other than `common sense’ of mathematical reasoning. Readers who are unfamiliar with the elementary knowledge of mathematical logic may refer to a very readable account by Margalis [21]. The propositions of the formal language in metamathematics are formulae built from finite number of symbols according to certain rules. In Gödel’s theorem, is a formal system of natural numbers called the Peano arithmetic which contains symbols such as 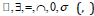. The meaning of each symbol (in metalanguage) is, ‘not (negation),’ ‘for some,’ ‘equal,’ ‘and,’ ‘zero,’ ‘plus one (successor),’ ‘left parenthesis,’ and ‘right parenthesis, respectively. Moreover, contains variables representing natural numbers, ‘,’ ‘,’ ‘z,’ and so on. The rules of structure of the propositions of are such that the interpretations of the propositions of will be declarative sentences which are not necessarily true of ‘ordinary discourse (metalanguage).’ For instance, the proposition 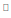∃x (0 =σ (x)) means that ‘there does not exist such a natural number (positive integer) that the successor of it is 0.’ This is a true proposition of Peano arithmetic and indeed this formula is one of its axioms. Logical inferences in is conducted according to modus ponens, meaning that for any formulae and in , follows from F→G and , where the formula F→G means ‘ implies ,’ and defined by F→G ≡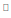 (F∩ 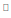G) . The ingenious technique developed by Gödel is that one assigns a (prime) number to each symbol of L: 1 to 0, 3 to σ , 5 to 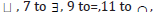13 to (and 17 to), and (pi)n (where pi’s are primes greater than 17) to the variables of type n, where the variables expressing the natural numbers are of type 1, the variables expressing the functions of natural numbers are of type 2, and so on. Having assigned numbers to symbols in this way, we next assign numbers to formulae: let n1, n2, … nk be the numbers of the symbols of a formula F in the order in which they occur in F. For example, let be 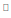∃x (P(x)∩ N (x)). Then the numbers are 5, 7, 191(=19), 13, 1, 9, 3, 13, 19, 17, 17. Let p1, p2, … pk be the first primes (starting from 2) in order of increasing magnitude. Then the number assigned to will be (p1)n1(p2)n2...(pk)nk. Then the Gödel number of 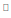∃x (0 =σ (x)) is determined as 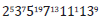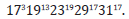By this procedure of Gödel numbering, we have established a one-to-one correspondence between the set of formulae in the formal system and a subset of natural numbers in the number system of (actual or of metalevel) arithmetic. Gödel’s fundamental discovery is that, cleverly using the recursive functions, which are functions from natural numbers that satisfy certain conditions, metamathematical concepts such as ‘axioms,’ ‘meaningful formulae,’ ‘proofs,’ and ‘provable formulae’ are all represented as formulae with the corresponding Gödel numbers in . The crucial fact which will be effectively used as proof of the incompleteness theorem is that in , we can construct a formula which means that ‘the formula with the Gödel number is a provable formula.’ Similarly, the formula meaning ‘the negation of the formula with the Gödel number is probable’ is defined.
A formal system is said to be consistent if there does not exist a formula such that and in. The formula (sentence) given by expresses that ‘there does not exist any formula such that it and its negation are both provable,’ or equivalently ‘the formal system (Peano arithmetic) is consistent.’ We are now ready to prove the incompleteness theorem, which asserts that there exist undecidable propositions in any consistent formal systems. For expository simplicity, however, we shall present the first incompleteness theorem for Peano arithmetic under the assumption that it proves only true propositions. This condition is called correctness. Note that if a formal system is correct, then is obviously consistent. Actual correctness is stronger than ω-consistency, which is stronger than the (simple) consistency and assumed in Gödel’s original proof of the (first) incompleteness theorem.
First Incompleteness Theorem (Weak Form): If Peano arithmetic is correct, there exists a formula which is not proved or disproved in.
Proof: In L, there exist countably many numbers of formulae with a variable 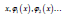with the Gödel number g1, g2, … respectively. Let NP(x)be a formula defined by NP(x) ≡ P(x) which means that ‘the formula with Gödel number is not provable.’ Because NP(x) also appears in the above list, we have for some , NP(x) =ϕk (x) with the Gödel number k g . Then the formula G ≡ϕk (gk) means that ‘the formula with the Gödel number k g is not provable,’ or equivalently, ‘ is not a provable formula.’ We now show that is the desired undecidable proposition. Indeed, suppose that ‘ is provable in .’ The assumption that ‘ is correct’ implies that ‘G is true.’ Hence, ‘G is not provable,’ which is a contradiction. Next, suppose that ‘ is provable.’ Then, 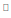G is true’ again by the correctness of , which implies that ‘ is provable.’ Then ‘G and 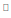G are both provable in L,’ which is a contradiction. Therefore, ‘G and 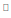G are both unprovable (G is undecidable).’ QED.
In the above proof, the statement ‘G is true’ is a consequence of the assumption that ‘L is correct.’ In the original proof of the first incompleteness theorem, Gödel showed that: ‘If L is consistent, then G is true.’ Recall that the formula 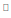∃x (P(x)∩ N (x)) expresses that ‘L is consistent,’ and call this formula Consis. Gödel also obtained a cerebrated corollary known as:
Second Incompleteness Theorem: If Peano arithmetic is consistent, Consis cannot be proved in .
Proof: We can formalize the statement (3) as a provable formula: Consis →G in L. Suppose that ‘Consis is proved in L.’ Then by modus ponens, we can prove the formula . But this contradicts that means ‘ is not a provable formula.’ QED.

1. Rawls called the ‘model’ a ‘device of representation’.
2. The order of statements (a) and (b) is reversed to that of the Theory. Our arrangement seems to be more convenient because of the (lexicographic) order of the principles.
3. The ideology of empiricism is the attitude that one tries to recognize a concept which is understandable only as a relationship between objects as a property to be proper and inherent for them. This ideology has been common and persistent among all people including philosophers. Indeed, it can be seen in the use (exchange) value of A. Smith or surplus value of K. Marx. These concepts of economic values are stipulated as proper and inherent properties of commodities, which are determined by the labor power required to produce them; see also note 9.
4. This sentence is that of ordinary mathematical question at the meta level, hence we do not put it in quotation marks.
5. Sometimes we say that ‘Gödel proved that mathematics has no logically firm grounds,’ suggesting that ‘(ordinary) number theory might be inconsistent, hence it was doubtful.’ Such statements, which seem to be unfortunately common among philosophers in the French theory [22], are plainly silly. As meta-theorems of metamathematics, the incompleteness theorems simply describe very interesting properties of Peano arithmetic, namely that it includes undecidable propositions and cannot prove a formula expressing its own consistency if it is consistent, nothing more. If you doubted the validity of, say, recursive functions, or other arithmetical concepts, or our ordinary arithmetical practices at the meta level, you could never understand or even follow the proofs of incompleteness theorems. By telling ‘nothing more,’ however, I do not mean that the incompleteness theorems have no impact on our mathematical practices at the metalevel. Indeed, the implications of incompleteness theorems, and the second incompleteness theorem, are taken seriously by almost all mathematicians and logicians: The significance of Gödel’s second theorem lies in the interpretation: If N (Peano arithmetic) is consistent, then the consistency of N cannot be proved by methods formalizable in N. Like the (first) incompleteness theorem, Gödel’s second theorem applies to many theories both weaker and stronger than N. It applies to set theory and every formal extension of N. Although the consistency of N can be proved in set theory, the value of the proof is doubtful, because set theory itself cannot be proved consistent by methods formalizable in set theory [21].
6. Husserl replies to their objections to phenomenology by invoking the ‘naïveness of scientists’ (cf. Crisis, Part II). We accept the proofs of incompleteness theorems given the validity of arithmetic and arithmetical concepts at the meta level. This is the usual attitude of mathematicians and logicians. Would Husserl call this attitude naïve? The way in which Husserl responded to incompleteness theorems is interesting, although he did not make any comments about them. On the other hand, his comments on ‘the origin of mathematical concepts’ seem to be surprisingly naïve. In §9 of Crisis and a famous unpublished manuscript ‘The Origin of Geometry (Appendix VI in Crisis; see also [16]),’ he likened it to our natural experiences in the lifeworld: It is now clear that even if we know almost nothing about the historical surroundings world of the first geometers, this much is certain as an invariant, essential structure: that it was a world of ‘things’ (including the human beings themselves as subjects of this world); that all things necessarily had to have a bodily character What is also clear, and can be secured at least in its essential nucleus through careful a priori explication, is that these pure bodies had spatio-temporal shapes and ‘material’ qualities (color, warmth, weight hardness, etc.) related to them. Further, in the life of practical needs certain particularizations of shape stood out and that a technical praxis always (aimed at) the production of preferred shapes and improvement of them according to certain directions of gradualness (ibid., 375). What Husserl seemed to overlook when he sought ‘the origin of the geometry’ was the definitive distinction of ontological levels of experiences and mathematical concepts. Even if we accepted those experiences as the origin of geometry in some sense, they would never reach the geometrical concepts continuously by ‘the growth of measuring technique’ (ibid, p. 376) or anything as such. Husserl would have rejected our view in metaphysical terms of ‘ontological levels.’ But it is doubtful whether his view is not about an ideological view of empiricism (see the note 13 below), or at least indeed to be ‘phenomenologically reduced.’ We even doubt whether ‘the origin of the geometry,’ in the sense of Husserl, really ‘exists. 7. Strictly speaking, epochē is not a device of representation, although it is certainly a philosophical method used by Husserl. It is a reduction entirely opposite to representation.
8. This is not obvious (cf. the note 6).
9. Ideologies were first discovered by K. Marx in the 1840s. As is well known, their most eminent form that he recognized was the ‘bourgeois ideology.’ The idea of ideologies was expanded on and explored by French Marxist L. Althusser in the 1960s. They no longer mean mere ‘mental forms of leisure class,’ or simple ‘prejudices or partial opinions’ for political matters, such they were seen in the Cold War era. According to Althusser, they are almost the equivalence of ‘frames of recognitions,’ meaning that all humans, including philosophers, look at, recognize, think, and believe through their ideologies. Therefore, ideologies spread across all realms of the lifeworld, including philosophers’ thoughts and problems: I should add that if it is not so much the immediate content of the objects reflected as the way the problems are posed which constitutes the ultimate ideological essence of an ideology, this problematic is not of itself immediately present to the historian’s reflection, for good reason: in general, a philosopher thinks in it rather than thinking of it, and his ‘order of reasons’ does not coincide with the ‘order of reasons’ of his philosophy. An ideology can be regarded as characterized in this respect by the fact its own problematic is not conscious of itself ([9,10], italics by Althusser). We believe that the idea (we do not call it a ‘concept,’ because we do not ‘understand’ ideologies) of ideologies is the most precious legacy of the Marxian tradition left to liberal philosophers, although we are certainly far from the state of ‘understanding’ them. We do not even know what ‘understanding ideologies’ really means.
10. Derrida [16] characterized mathematical objects as such. He emphasized that these characters of mathematical objects made them the ‘privileged examples and most permanent threads guiding Husserl’s reflection [17].’
11. Recall our meta-theorem concerning the nonexistence of natural rights. At the same time, we can interpret this meta-theorem as a proposition which makes clear the ideological nature of the natural right. It is a (n ideological) concept generated by an ideology that confuses relations, such as rights, with entities, such as moral characteristics.
12. This is indeed the case for justice as fairness itself. Recall that the two principles of justice were discovered through careful examination and exploitation of the utilitarian principle by Rawls (see Rawls’s statements at the end of the next section).
13. Note that they are formal symbols in L which should be distinguished from ordinary parenthesis in the text.
14. Note that formulae in L as such are just stringing of symbols such as 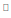,∃, x and so on, but generally they represent their (metamathematical) meanings in our ordinary discourse (metalanguage). Recall that our example of the formula 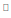∃x (0 =σ (x)) has the meaning ‘there does not exist such a natural number that the successor of it is 0’ in metalanguage (ordinary English). In what follows, we put the (metamathematical) meanings into quotation marks.
15. A sentence is a formula that contains no free variable. A variable in a formula is said to be free if its occurrence in the formula does not associate with the symbol ∃. For instance in th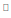e formula, (σ (x) = x) , the variable x is free. However, in the formula: 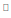∃x (σ (x) = x) , the variable x is not free (bounded); see Margalis [21].
16. The existence of G is a formal result obtained in L. G is a sentence called the Gödel sentence?

1. Rawls J (1971) A theory of justice. Harvard University Press, USA.
2. Rawls J (2001) Justice as fairness: a restatement, Harvard University Press, USA.
3. Arrow K, Debreu G (1954) Existence of an equilibrium for a competitive economy. Econometrica 22(3): 265-290.
4. Neumann J, Morgenstern O (1944) Theory of games and economic behavior. Princeton University Press, USA.
5. Nash JF (1950) Equilibrium points in n-person games. Proceedings of the National Academy of Sciences of the USA 36(1): 48-49.
6. Arrow K (1963) Social choice and individual values. Wiley, USA.
7. Gödel K (1931) Űber formal unentscheidbare sätze der principia mathematica und verwandter systeme i. Monatshefte für Mathematik und Physik 38: 173-198.
8. Hart HLA (1955) Are there any natural rights? The Philosophical Review 64(2): 175-191.
9. Althusser L (1965) Pour marx, françois maspero, paris; for marx. Verso, USA.
10. Althusser L, Balibar E (1968) Lire le capital, françois maspero, paris; reading capital, Verso, USA.
11. Husserl E (1954) Die Krisis der europäishen Wissenshaften und die transzendentale Phänomenologie: Eine Einleitung in die phä Northwestern University Press, USA.
12. Arrow K (1973) Some ordinalist-utilitarian notes on rawls’s theory of justice. The Journal of Philosophy 70(9): 245-263.
13. Hart HLA (1973) Rawls on liberty and its priority. University of Chicago Law Review 40(3): 534-555.
14. Rawls J (1993) Political liberalism. Columbia University Press, USA.
15. Harsanyi J (1975) Can the maximin principles serve as a basis for morality? a critique of john rawls’s theory. American Political Science Review 69(2): 594-606.
16. Derrida J (1962) Introduction à ‘l’ origine de la géométrie de husserl, Presses Universitaires de France, France.
17. Derrida J (1967) La voix et le phénomè Presses Universitaires de France, France.
18. Nozick R (1974) Anarchy, state and utopia, Basic Books, USA.
19. Rosser B (1939) An informal exposition of proofs of gödel’s theorems and church’s theorem. The Journal of Symbolic Logic 4(2), 53-60.
20. Gödel K (1931) On undecidable sentences. Oxford University Press, UK, 31-35.
21. Margalis A (1990) First order mathematical logic, Dover, USA.
22. Socal A, Bricmont J (1999) Fashionable nonsense: postmodern intellectual’s abuse of science, Picador, UK.