Tax Evasion Dynamics via Equilibrium and Non-Equilibrium Models on Solomon Networks

Zaklan et al. [1] proposed a model to study the fluctuation tax evasion on agent-based community close to critical points. Zaklan used the equilibrium Ising model on a square lattice and Monte- Carlo simulations with the Glauber algorithms as a dynamic of temporal evolution. Zaklan et al. [2] considered a large number of agents (people) who interact locally with their neighbours and base their decision whether to evade taxes or not on the behaviour of their neighbours. In the study of tax evasion, they used the Ising model on a square lattice. Their results are in excellent agreement with analytical and experimental results obtained by [3].

Lima [4] studied the tax evasion fluctuations via a nonequilibrium model where each agent has an opinion in the presence of a social noise (q) as in Majority-vote model (MVM) [5]. Hokamp & Pickardt [6] and Pickhardt & Seibold [7], argued that any agent- based tax evasion model may ac- cording to their characterization may fall into the economics domain or into the econophysics domain. Then, Pickhardt and Seibold classify the Zaklan model as an econophysics model, because the model evolves by statistical mechanics using an Ising model or MVM.

The Solomon networks (SNS) [8-10] are formed by two types of neighbours, the neighbours at home and neighbours in the workplace. Thus the home neighbourhood is different and the workplace neighbourhood. These neighbor- hoods are formed by two chains of L sites each, the home chain and the workplace chain. Therefore, there are three components of interaction:

1) The nearest-neighbor interaction among different agents on the home chain,

2) The nearest-neighbor interaction among different agents on the workplace chain and

3) The interaction between the variables corresponding to the same agent in two chains.

Then, the same agent occupies two chains of L size lattice with N=2L sites. In this work, we study the problem of the tax evasion on an agent s com- munity of honest citizens and tax evaders, where the agents are positioned on sites of SNS via the Ising model and MVM.

Ising model

We consider the ferromagnetic Ising model, on SNS by a set of spins variables σ_i = ±1 situated on every site i of a SNS with N=2L sites, where L is the size of each chain similar to Malarz [8]. The evolution in time of these systems is given by a single spin-flip like heat bath dynamics with a flip probability p given by

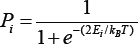
Where T is the temperature, K_B is the Boltzmann constant and E_i is the energy of spin ai obtained from

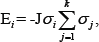
Where the sum runs over all neighbours k of i with k=4 on SNS. In the above equation J is the exchange coupling.

We study the MVM on SNS using the probability wttL as a function of the social temperature T called Glauber rate probability The Glauber transition rate of MVM can be written as

Where S(x≠0) is the sign ±1 of x and S(0) β_r is the inverse of the temperature 1/kBT . The sum runs over the k (k=4 for SNS) neighbors j of spin i.

The opinion of a people community per total number of people is given by

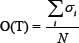
In order to model tax evasion, we further use for all agents one probability pa of an efficient audit. If tax evasion, σ_i=-1, is detected by this audit, the agent must remain honest, σ_i= +1, for a number k of time steps. Again, one time-step is one sweep through the entire network.

For to get the control of the tax evasion dynamics we use the fraction of tax evaders given by

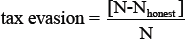
Where N is the total number and N_honest the honest number honest of agents. The tax evasion is calculated at every time to step t of system evolution.

Figure 1: Baseline case: k=0 and pa=0% in (a), k = 1 and pa=0:5%, k = 10 and pa=4:5% (normal case in Germany), and k=50 and pa=90% (extreme case) and we did all simulations over 20; 000 time steps, also in the later gures. Here, we use N=800 sites.

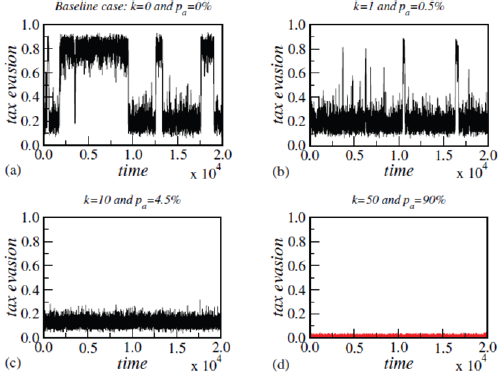
For both Ising model (Figure 1) and MVM (Figure 2) we set a fixed noise (T), where T=0.95Tc with Tc=6.985 Ising model and Tc=1.915 (MVM) such that we see flips of the whole system in the baseline cases k=pa=0. Then we vary the degrees of punishment (k=1, 10 & 50) and audit probability rate (pa=0.5%, 10% and 90%). If tax evasion is detected by an audit, the enforcement mechanism pa and the time of punishment k control the tax evasion level. The punished individuals remain honest for a certain number k of periods.

Following the same steps as we did in a previous work [4], we first will present the baseline case k = 0 and pa = 0.0%, i.e., no use of enforcement, at T=0.95Tc and with N=800 sites for Ising model (Figure 1) and MVM (Figure 2). All simulation for N=800 sites is performed over 20, 000 time steps, as shown in Figure 1 & 2. For very low T the part of autonomous decisions almost completely disappears. The individuals then base their decision solely on what most of their neighbours do. A rising noise has the opposite effect. Individuals then decide more autonomously.

Figure 2: As in Figure 1, but now for MVM.

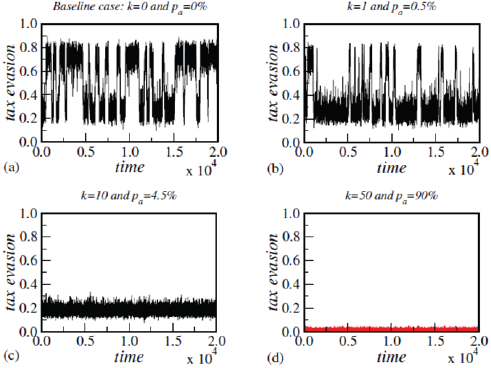
Figure 3: Tax evasion for Ising model on SNS networks and degrees of pun-ishment k%1, 10 & 50 and audit probability pa=0:5%, 10% and 90%.

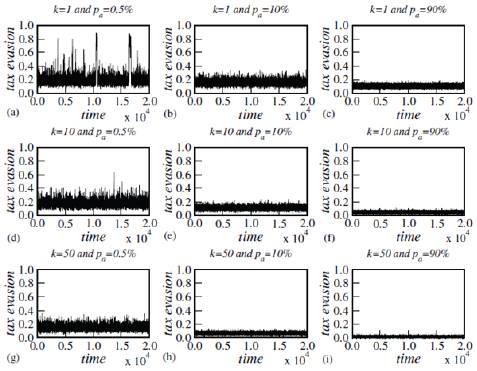
Figure 4: The same of the Figure 3, but now to MVM.

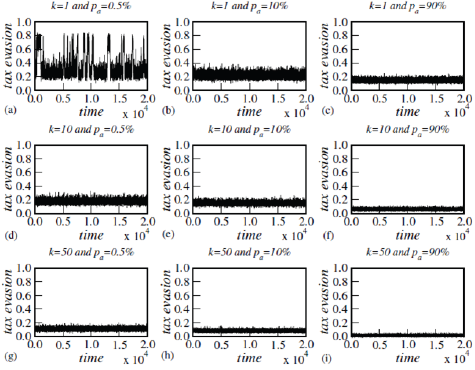
Figure 3 & 4 display different simulation settings for Ising model and MVM on SNS, for each considered combination of degree of audit probability (pa=0.5%, 10% and 90%) and punishment (k=1, 10 & 50), where the tax evasion is plotted over 20, 000 time steps. Both a rise in audit probability (greater pa) and a higher penalty (greater k) work to flatten the time series of tax evasion and to shift the band of possible non-compliance values towards more compliance. However, the simulations show that even extreme enforcement measures (pa=90% and k=50) cannot fully solve the problem of tax evasion.

In this work, we used the Ising and Majority-Vote models for the temporal evolution dynamics of the Zaklan model. These models explore the effect of a topology as Solomon networks. On Solomon networks a person or agent- based can be influenced by two types of neighbourhood, where the neighbours at home differ from the neighbours in the workplace except when everybody works at home. The Zaklan model of tax evasion can be evolved by dynamic equilibrium as the Ising model [1,2] and non-equilibrium Majority-vote [4] model and also on various topologies [11]. The Zaklan model incorporates concepts from econophysics; we argue here that Solomon networks are a good framework for simulating Zaklan model where taxpayers always make a prior consultation with their neighbours before making any final decisions. Here, we obtain identical results for both models Ising and Majority-Vote model in the control of the tax evasion on Solomon networks; where for any other topologies behaviour of these models is different. These results agree with the criteria from Grinstein et al. [12] where non-equilibrium stochastic spin systems, on square lattice with up-down symmetry, fall into the same universality class as the equilibrium. Here, we also found plausible result that tax evasion is diminished by higher audit probability pa and stronger punishment k on Solomon networks.

The authors would like to thank the Brazilian agencies CNPq and Capes. The authors are also in debt to the referees, who have given several suitable suggestions for a real improvement of the present manuscript

1. Zaklan G, Westerhoff F, Stauffer D (2009) Analysing tax evasion dynamics via the Ising model. J Econ Interact Coordination 4: 1.
2. Zaklan G, Lima FWS, Westerhoff F (2008) Physica A: Statistical mechanics and its applications 387(23): 5679-5962.
3. Wintrobe R, G'erxhani K (2004) Tax evasion and trust: A comparative analysis. Proceedings of the anuual meeting of the European public choice society 6(4): 15-18.
4. Lima FWS (2010) Analysing and controlling the tax evasion dynamics via majority-vote model. Journal of physics: Conference Series 246: 012033.
5. Oliveira MJ (1992) Isotropic majority-vote model on a square lattice. J Stat Phys 66(1-2): 273-281.
6. Hokamp S, Pickardt M (2010) International Economic Journal 24: 541.
7. Pickhardt M, Seibold G (2014) Income tax evasion dynamics: Evidence from an agent-based econophysics model. Journal of Economic Psychology 40(2014): 147-160.
8. Malarz K (2003) Desitter gauge theory of gravitation. Int J Mod Phys C 14(1): 561.
9. Erez T, Hohnisch M, Solomon S (2005) Economics: Complex Windows. Springer Milan, pp. 201- 217.
10. Goldenberg J, Shavitt Y, Shir E, Solomon S (2005) Distributive immunization of networks against viruses using the 'honey-pot' architecture. Nature Physics 1: 184-188.
11. Lima FWS (2012) Controlling the tax evasion dynamics via majority- vote model on various topologies. TEL 2(1): 87-93.
12. Grinstein G, Jayaprakash C, Yu He (1985) Statistical mechanics of probabilistic cellular automata. Phys Rev Lett 55(23): 2527.