Nonlinear Dynamical Structures on Coupled Duffing-Van der Pol Oscillators with Two Degrees of Freedom by New Approach AGM

Introduction

In dynamics, the Van der Pol and Duffing oscillator is a nonconservative oscillator with non-linear damping so in this literature is solved complicate differential equation in the dynamic system by new approach AGM [1-11]. Therefore, most of the engineering problems are nonlinear so in most cases it is difficult to solve of analytically and analyze these equations. The equations governing on the motion of engineering systems lead to the ordinary or partial differential equations and among different fields of engineering problems, the equations governing on the oscillation systems are significantly nonlinear and as a result much attention has been devoted to this area and various researches have been done up to now [12]. Recently, many authors used various analytical methods for solving nonlinear oscillation systems. Some of these well-known methods are introduced for instance: bookkeeping parameter perturbation method [13], energy balance method [14], amplitude frequency formulation [15], max-min approach [16,17] and Mickens iteration procedure [18].

Some analytical methods like perturbation techniques are only applicable if small parameters exist in the nonlinear systems where this solution can analytically be expanded into a power series of parameters. Inasmuch as a lot of nonlinear problems do not contain such perturbation quantity and in order to overcome this shortcoming, many new approaches have been appeared for instance, harmonic balance method (HBM) [19,20], the elliptic Lindstedt-Poincare method (LP) [21], the Krylov Bogolioubov Mitropopolsky method (KBM) [22], Adomian decomposition method [23] and homotopy perturbation method (HPM) [24]. Another powerful analytical method, called the variational iteration method (VIM) which was first proposed by He [25-27]). VIM has successfully been applied to solve various engineering applications. For example, the classical Blasius‟ equation was solved by using VIM and also this method was utilized to give approximate solutions for some well-known non-linear problems. Furthermore, many authors [28] used VIM to solve nonlinear equations governing on the oscillating systems. Another analytical method called the He‟s Amplitude Frequency Formulation method [29,30] which was first presented by Ji-Huan He. This method rapidly gives convergent successive approximations of the exact solution. He used HAFF to give approximate solutions for some well-known nonlinear problems.

The analytical method (Akbari-Ganji’s Method (AGM)).

A. Vibrational systems without any external force F (t ) = 0

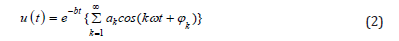
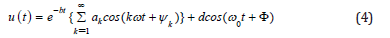
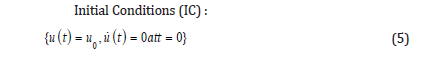
Note: At the vibration problems a sentence Eqs.(2) or (4) is sufficient accuracy so Eqs(3,4) rewritten as follows :

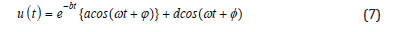
Selecting the answer of the governing equation for solving differential equations by AGM

In AGM, a total answer with constant coefficients is required in order to solve differential equations. As it is shown in Table 1 or Eqs.(6) or (7).

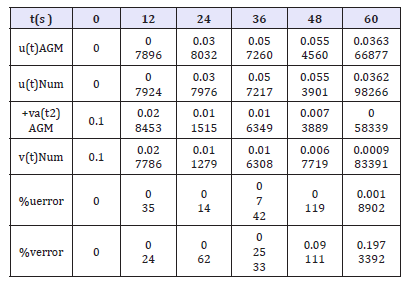
Table 1:The obtained Numerical Solution of Eqs (15) based on the given physical values Eqs (29).

Application of initial conditions to compute constant coefficients is done in two steps by AGM

Apply initial conditions in AGM method for vibrational systems at case of generally can be divided in two parts as follows:

a. Applying the initial conditions on the answer of differential equations:

It is notable that IC is the abbreviation of introduced initial conditions of Eq.(5).

b. Appling the initial conditions on the main differential equation and its derivatives:

Assume the general equation of vibrational systems:

According to Table 1 the suitable answer can be chosen as follow:

Afterwards Eq.(8) will be substituted into Eq.(9) instead of u as follows :

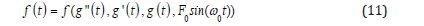
Eventually, the application of initial conditions on Eq.(11) and it derivatives is expressed as follows :

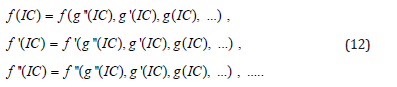
Finally, after applying the initial conditions on answer function Eq.(8), and also the function differential equation and on its derivatives from Eqs.(12) a set of algebraic equations which is consisted of n equations with n unknowns is created. Therefore, the constant coefficients of Eq.(3)or (4) which are {a1, a2 ,...,ϕ1,ϕ2 ,..., b,ω, d,φ} or the constant coefficients {a,b,d} and angular frequency ω and initial phase (ϕ andφ ) at Eqs. (6)or (7) are will easily computed in AGM by applying the initial conditions of Eq.(5).

Application

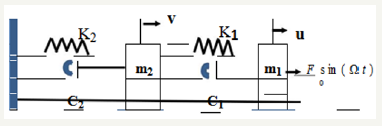
According Figure 1 governing nonlinear differential equations which is shown by the Van der Pol and Duffing equation as follows:

Figure 1:The schematic diagram of the physical model.

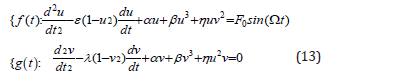
Then, the initial conditions are expressed in the forms of :

Solving the differential equation with AGM On the basis of the given explanations in the previous section, the answer of Eq.(13) in AGM is considered as follows

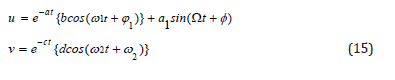
The constant coefficients of Eqs.(15) which are ω (angular frequency), ϕ (initial vibrational phase) a,a1,b,c,d can easily be gained by applying the initial conditions or boundary conditions.

Applying initial or boundary conditions in AGM

We consider the proposed physical model along dynamical system whit two Degrees of Freedom as follows: The constant coefficients of Eqs.(15) can be obtained by applying the initial or boundary conditions in two ways in AGM as follows:

Generally, the initial conditions are applied on Eqs.(15) in the forms of:

For simplicity, IC is considered as the abbreviation of the initial conditions. As a result, applying the initial conditions on Eqs.(15) is done as:

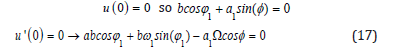
As well as:

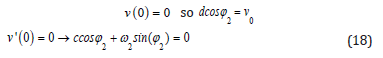
The application of initial or boundary conditions on the main differential equation f(t ), g (t ) which in this case is Eqs.(13) and its derivatives f (n)(t ) , g n(t ) is done in the following general form:

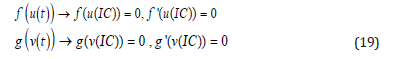
Therefore according to Eqs.(19), the initial conditions are applied after substituting Eqs.(15) which has been considered as the answer of the main differential equation into Eqs.(13) as follows:

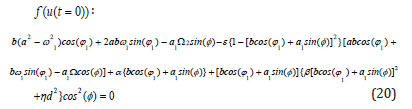
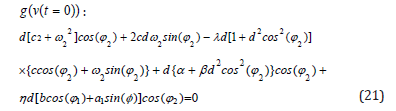
The application of initial conditions on the its derivatives in the forms of:

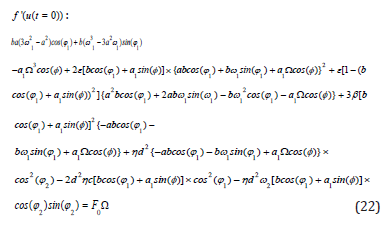
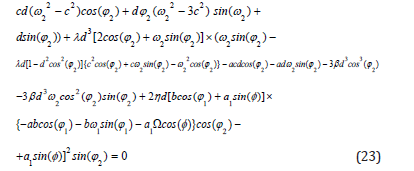
Applying initial conditions on the second and third derivatives f (t ) is same as previous and as follows:

By solving a set of algebraic equations which is consisted of ten equations with ten from Eqs.(17-18) and Eqs.(20-24), the constant coefficients of Eqs.(15) can be yielded as:

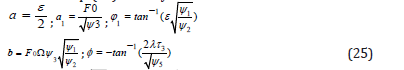
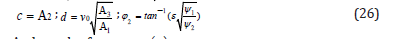
And angular frequency (ω)

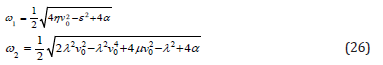
By substituting the above parameters into Eqs.(15), the answer of the couple nonlinear differential Eqs.(13) is obtained in the form of:

Numerical Solution

With regard to the given physical values from Eq.(29) and the determined domain t∈{0,60} which is defined in terms of second (sec) , the solution of the differential equation is expressed numerically in the following Table 1:

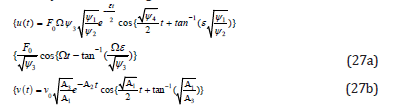
The following above parameters of Eqs. (27a,27b) are introduced as:

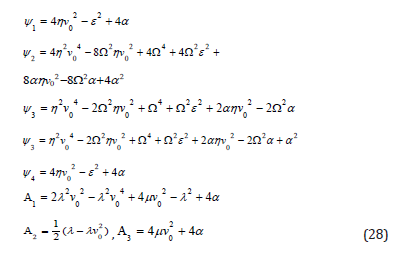
By selecting the physical values of vibration below:

According to physical values Eqs.(29) the solution of Eqs. (27a,27b) and the angular frequency Eqs.(26) are rewritten as follows:

Comparing the achieved solutions by numerical method and AGM

Figure 2:Comparing the obtained solutions by AGM and numerical method for (u) .

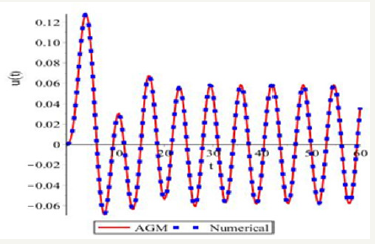
Figure 3:Comparing the first derivative of the obtained solutions by AGM and Numerical Method for (u).

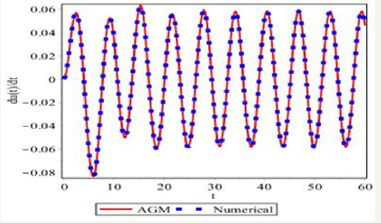
Due to the obtained results from solving Eqs.(15) by AGM, which is expressed by Eqs.(27a,27b), and the obtained Numerical Solution which its results have been presented in Table 1, we will have the following comparisons: With regard to Figure 2-8, it is obvious that AGM is an accurate and acceptable method for solving nonlinear differential equations and so it is obviously that the charts of AGM and Numerical solutions are overlapped, this overlap represents precision of the AGM method at the solution of nonlinear equations.

Figure 4:Comparing the related phase planes of the achieved solutions by AGM and numerical method.

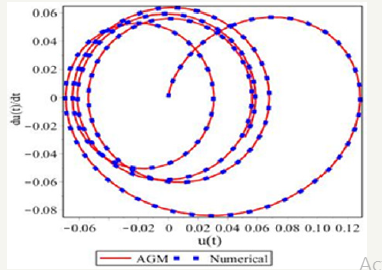
Figure 5:Comparing the obtained solutions by AGM and numerical method for (v ) .

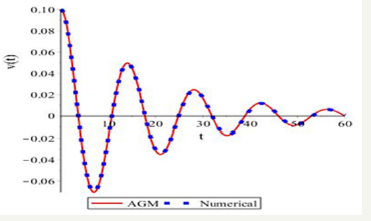
Figure 6:Comparing the first derivative of the obtained solutions by AGM and numerical method for (v).

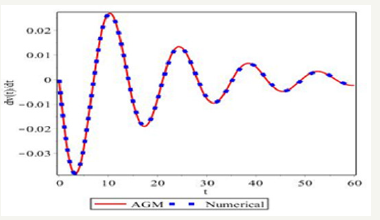
Figure 7:Comparing the related phase planes of the achieved solutions by AGM and Numerical Method..

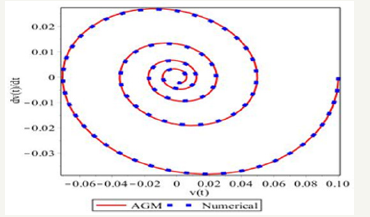
Figure 8:The chart of angular frequency in terms of initial vibrational amplitude.

Conclusion and Discussion

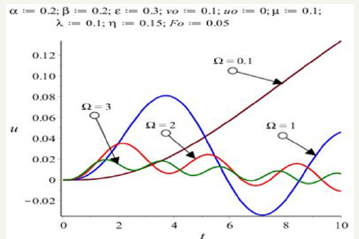
Figure 9:The chart of angular frequency in terms of initial vibrational amplitude.

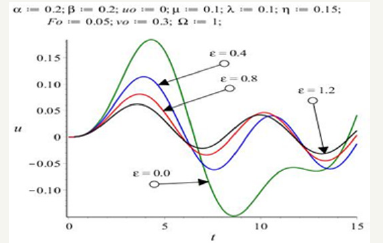
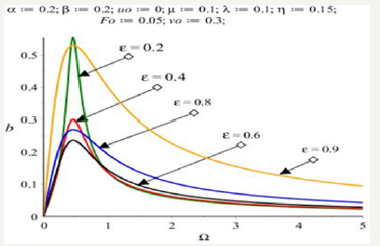
The displacement vibratio amplitude (ʋ) from Eqs.(27a) in terms of angular frequency of external force (Ω) of vibration is illustrated as follows: As regards Fig.8, it is resulted that by increasing the parameter of the angular frequency of external force (Ω), the amount of the displacement vibration amplitude is significantly decreased. At the above Figure 9 , the effect of the parameter of damping coefficient (ε) on the amount of the displacement vibration amplitude has been significantly decreased. Eventually based on the achieved observation from Figure 10, it is clear that by choosing specified values of the damping coefficient (ε) and angular frequency of external force (Ω) can be make vibrational system into the resonance state.

Figure 10:The chart of angular frequency in terms of initial vibrational amplitude.

The difference between obtained solutions by AGM and numerical method

Figure 11:The chart of angular frequency in terms of initial vibrational amplitude.

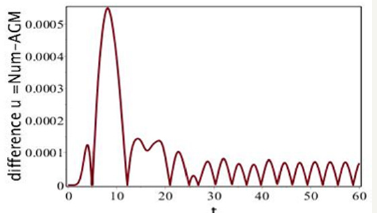
Figure 12:The result of difference between the obtained solutions by AGM and numerical method for v(t).

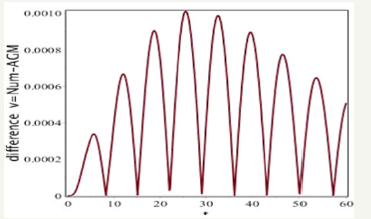
The following charts indicate the difference between the obtained solutions by AGM and Numerical Method as follows: In accordance with Figure 11 and Figure 12, the difference between the obtained solution by AGM and numerical method (rkf-45) is very negligible which proves the reliability of this technique.

Conclusion

In this paper, one complicated nonlinear vibrational partial differential equations have been introduced and analyzed completely by Algebraic Method (AGM) and also the obtained results have been compared with Numerical Method (Runge- Kutte 4th). The above process has been done in order to show the ability of AGM for solving a broad range of differential equations in different fields of study particularly in vibrations. Consequently, it is concluded that AGM is a reliable and precise approach for solving miscellaneous differential equations. Moreover, a summary of the AGM excellence and benefits is explained as: By solving a set of algebraic equations with constant coefficients, we are able to obtain the solution of nonlinear differential equation along with the related angular frequency simultaneously very easily which applying this procedure is possible even for students with intermediate mathematical knowledge. On the other hand, it is better to say that AGM is able to solve linear and nonlinear differential equations(ODE , PDE) directly. Therefore, AGM can be considered as a significant progress in nonlinear sciences. Inasmuch as the shortage of boundary condition(s) in this method for solving differential equation(s) is completely terminated, AGM is operational for miscellaneous nonlinear differential equations especially for the vibrations of civil engineering and Mechanical machinery and we are hopeful this method will be applied by enthusiastic young researchers in the near future.

Acknowledgment

AGM method has invented by Mohammadreza Akbari in 2014 and I am hope it will be serviced to all researchers in the engineering world, and as well as I am grateful to all everyone who helped me inany way possible in development this creation. We can certainly claim which AGM method can be very beneficial and high efficiency for analytical solving the set of coupled nonlinear differential equations (ODE,PDE) at the practical field in engineering industries and basic sciences.

References

1. Akbari R, Ganji DD, Nimafar M, Rostami AK (2015) Solution of the nonlinear governing differential equation of a vibrating rod with attached mass, by the AGM. KSCE Journal of Civil Engineering 00(0): 1-9.
2. Akbari MR, Ganji DD, Nimafar M (2014) Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Frontiers of Mechanical Engineering Journal 9(4): 390-401.
3. Rostami AK, Akbari MK, Ganji DD, Heydari S (2014) Investigating Jeffery- Hamel flow with high magnetic field and nanoparticle by HPM and AGM. Cent Eur J Eng 4(4): 357-370.
4. Akbari MR, Ganji CC, Majidian A, Ahmadi AR (2014) Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM. Frontiers of Mechanical Engineering 9(2): 177-190.
5. Ganji DD, Akbari MR, Goltabar AR (2014) Dynamic vibration analysis for non-linear partial differential equation of the beam-columns with shear deformation and rotary inertia by AGM. Development and Applications of Oceanic Engineering.
6. Akbari MR, Ganji DD, Ahmadi AR, Sayyid H, Kachapi H (2014) Analyzing the nonlinear vibrational wave differential equation for the simplified model of tower cranes by (AGM). Frontiers of Mechanical Engineering 9(1): 58-70 .
7. Akbari MR, Nimafar M, Ganji DD, Akbarzade MM (2014) Scrutiny of nonlinear differential equations Euler-Bernoulli beam with large rotational deviation by AGM Springer. Frontiers of Mechanical Engineering 9(4): 402-408.
8. Akbari MR, Nimafar M, Ganji DD, Ahmadi AR (2014) Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Front Mech Eng 9(4): 390-401.
9. Mirgolbabaee H, Ledari ST, Ganji DD (2016) New approach method for solving duffing-type nonlinear oscillator. Alexandria Engineering Journal 55(2): 1695-1702.
10. Soheil TL, Hadi M, Davood DG (2015) Heat transfer analysis of a fin with temperaturedependent thermal conductivity and heat transfer coefficient. New Trends in Mathematical Sciences 3(2): 55-69 .
11. Mirgolbabaee H, Tahernejad SL, Ganji DD (2016) An assessment of a semi analytical AG method for solving nonlinear oscillators. New Trends in Mathematical Sciences, BISKA, NTMSCI 4(1): 283-299.
12. Hagedorn P (1988) Non-linear oscillations, clarendon. Translated by Wolfram Stadler, Oxford, UK.
13. Huan JH (2001) Bookkeeping parameter in perturbation methods. Int J Nonlinear Sci Numer Simul 2(3): 257-264.
14. Huan JH (2006) Some asymptotic methods for strongly nonlinear equations. Int J Mod Phys B 20(10): 1141-1199.
15. Huan JH (2008) Maxmin approach to nonlinear oscillators. Int J Nonlinear Sci Numer Simul 9(2): 207-210.
16. Huan JH, Chengtians H (2004) inequality and its applications. Appl Math Comput 151(3): 888-891.
17. Mickens RE (1987) Iteration procedure for determining approximate solutions to non-linear oscillator equation. J Sound Vib 116: 185-188.
18. Beléndez A, Hernández A, Beléndez T, Álvarez ML, Gallego S, et al. (2007) Application of the harmonic balance method to a nonlinear oscillator typified by a mass attached to a stretched wire. J Sound Vibration 302(4- 5): 1018-1029.
19. Beléndez A, Pascual C, Méndez D, Neipp C (2008) Solution of the relativistic (an) harmonic oscillator using the harmonic balance method. J Sound Vibration 311(3-5): 1447-1456.
20. Navarro JF (2007) On the implementation of the poincare-Lindstedt technique. Journal of Sound and Vibration 301: 415-419.
21. Krylov N, Bogolioubov N (1943) Introduction to nonlinear mechanics, Princeton University Press. Princeton, USA.
22. Ghosh S, Roy A, Roy D (2007) An adaptation of adomian decomposition for numeric-analytic integration of strongly nonlinear and chaotic oscillators. Computer Methods in Applied Mechanics and Engineering 196 (4-6): 1133-1153.
23. He JH (2004) The homotopy perturbation method for nonlinear oscillators with discontinuities. Applied Mathematics and Computation 151(1): 287-292.
24. He JH (1998) Approximate analytical solution of blasiu‟s equation. Commun Nonlin Sci Numer Simul 3(4): 260-263.
25. Huan JH (1999) Variational iteration method- a kind of non-linear analytical technique: some examples, Int J Non-Linear Mech 34(4): 699- 708.
26. Huan JH, Wan YQ, Guo Q (2004) An iteration formulation for normalized diode characteristics. Int J Circ Theory Appl 32: 629-632.
27. He JH (2006) Some asymptotic methods for strongly nonlinear equations. Int J Modern Phys B 20(10): 1141-1199.
28. Rafei M, Ganji DD, Daniali H, Pashaei H (2007) The variational iteration method for nonlinear oscillators with discontinuities. Journal of Sound and Vibration 305(4-5): 614- 620.
29. He JH (2008) An improved amplitude-frequency formulation for nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation 9(2): 211.
30. Ren ZF, Liu GQ, Kang YX, Fan HT, Li HM, et al. (2009) Application of hes amplitude frequency formulation to nonlinear oscillators with discontinuities. Physica Scripta 80: 45003